두 개 뽑아서 더하기
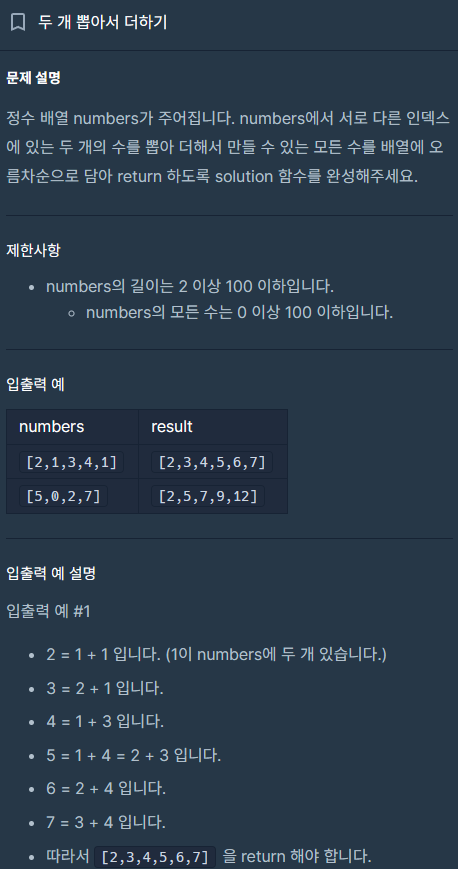
뭔가 하나하나 다 더해야하는데 더 좋은 방법이 없을까?...
특히 이중 반복문을 써야만 할건데 안쓰는 방법이 필요하다.(시간 복잡도에서 한 차원이 차이나버린다.)
안떠오른다.
나의 풀이
function sol01(numbers) {
var answer = [];
const length = numbers.length;
let i = 0;
while (i < length){
let j = i+1;
while ( j < length){
answer.push(numbers[i]+numbers[j])
j++
}
i++
}
answer = Array.from(new Set(answer)).sort((a,b)=> a-b)
return answer;
}while로 짜긴했지만 어제의 것에 이어서 for와 while의 속도를 비교할 것이기 때문에 for문 버전으로도 짤 것이다.
다른 사람의 풀이
function sol11(numbers) {
var answer = [];
numbers.forEach((v) => {
const num1 = numbers.slice();
let a = num1.indexOf(v);
num1.splice(a, 1);
num1.forEach((z) => {
let num2 = v + z;
if (!answer.includes(num2)) {
answer.push(num2);
}
});
});
return answer.sort((a, b) => a - b);
}forEach라는 반복문안에 또 같은 반복문을 넣어서 이것도 일 것이다.
여기서 확인해볼만한것은 요소를 하나하나 넣을때 중복 요소를 제거하는것과 마지막에 set으로 확인하는것의 속도 차이일 것이다.
속도 비교
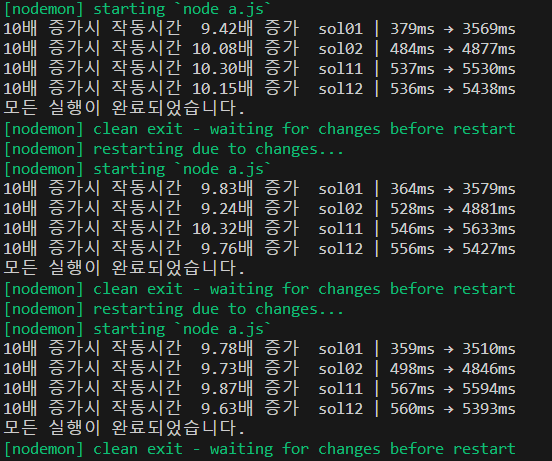
- 어제처럼 for문 보다 while문이 더 빠르다.
- 중복값 제거를 push하기 전에 하든, 넣을 거 다 넣고 set으로 하든 속도 차이는 없다.
그리고 의 시간복잡도임에도 10배가 증가한다. 아마 내가 충분히 큰 처리값을 주지 못한것같다.
const a = [1, 89, 3, 7, 2, 3, 863, 489, 3, 72, 328, 4]; 이건 너무 작은듯하니 더 크게 만들자.
async function main() {
const length = 100;
const maxValue = 1000;
const a = Array.from({ length }, () => Math.floor(Math.random() * maxValue));
await runSolutionWithTiming(sol01, a);
await runSolutionWithTiming(sol02, a);
await runSolutionWithTiming(sol11, a);
await runSolutionWithTiming(sol12, a);
}여기에 반복횟수는 1000 > 10000 회로 했다.
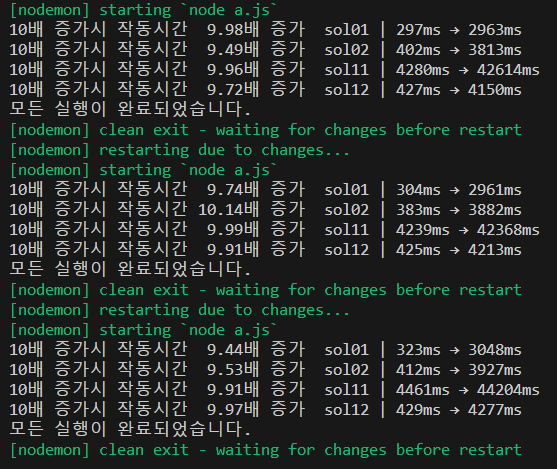
부하가 큰 경우에는 다른 사람의 풀이가 생각보다 느리다.
let a = num1.indexOf(v);
num1.splice(a, 1);시작점을 정할때 indexOf는 특정한 위치를 지정하는 것이 아니라 배열을 탐색하고 특정 지점을 찾아내는 방식이라서 처리해야할 배열의 길이야 요소의 크기가 클수록 더 느려지는 것같다.
numbers[i] + numbers[j]는 특정한 위치를 지정해주기 때문에 배열의 길이나 요소의 크기에 영향을 받지 않는다.
다음 큰 숫자

왜이렇게 이진법 문제가 많이 나오지? 컴퓨터라서 그런가?
나의 풀이
function sol0 (n) {
let N = n.toString(2)
const length = N.length
let n1 = 0
let i = 0
while (i <= length) {
if (N[i] === '1'){
n1 ++
}
i++
}
let k = N
let k1= 0
while (k1 !== n1){
k = (parseInt(k,2) + 1).toString(2)
const length2 = k.length
k1 = 0
i = 0
while (i < length2) {
if (k[i] === '1'){
k1 ++
}
i++
}
}
k = parseInt(k,2)
return k;
}두 번째 while문 안에서 while (i < length2) 로 돌렸는데 자꾸 일부 케이스에서 오류가 났다.
다시 생각해보니 다른 숫자에 대해서 반복문을 돌려야하기 때문에 아래와 같이 고쳤다.
k = (parseInt(k,2) + 1).toString(2)
const length2 = k.length
k1 = 0
i = 0
while (i < length2) {경험상 반복문 안에 반복문을 넣는 것은 시간복잡도에서 손해를 보기 때문에 굳이 분리하였다.
분리하지 않았다면 시간 복잡도가 이라는 끔찍한 결과가 나왔을 것이다.
현재 시간 복잡도는
다른 사람의 풀이
function sol1(n,a=n+1) {
return n.toString(2).match(/1/g).length == a.toString(2).match(/1/g).length ? a : sol1(n,a+1);
}정규식과 재귀 함수를 사용해서 매우 우아하게 풀어냈다.
시간 복잡도는
function sol2(n) {
var size = n.toString(2).match(/1/g).length
while(n++) {
if(size === n.toString(2).match(/1/g).length) return n
}
}무한 while 루프를 만든 뒤 1의 갯수가 같다면 return으로 탈출한다.
시간 복잡도는 .toString(2) 때문에 이라고 한다.
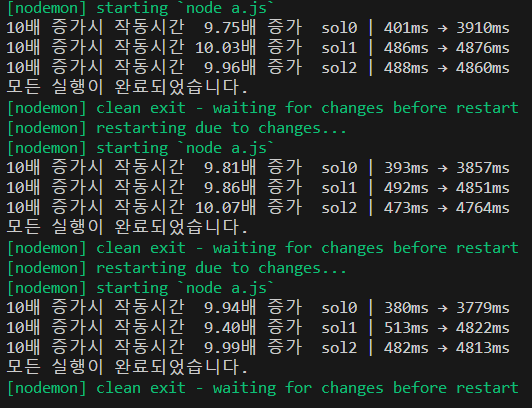
모두 최악의 경우에 의 시간복잡도를 가지지만 다행히 정도로 나왔다.
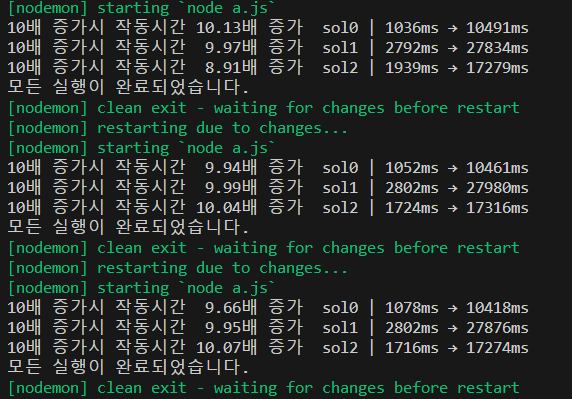
반복 횟수와 자릿수를 늘렸다. (얼마큼인지는 기록을 안해서 까먹었다 ㅠㅠ)
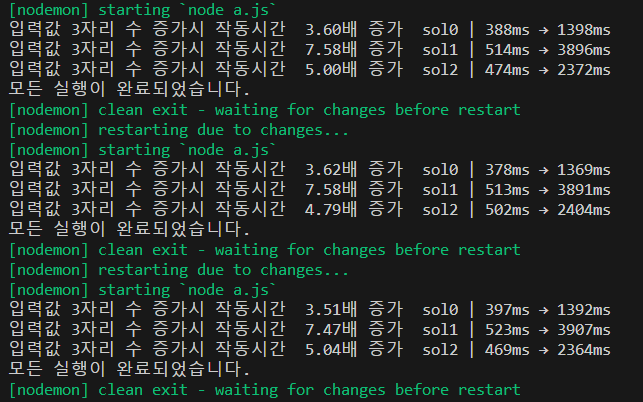
이제보니 반복횟수보다는 입력값을 변화 시키는 것이 더 유의미한 변화를 볼 수 있을 것같아서 그렇게 해보았다.
- 정규식을 쓰지 않는 것이 더 빠르다.
- 재귀함수를 쓰지 않는 것이 더 빠르다? 라고 잠정 결론을 내릴 수 있다.
공부하며 느낀 점
- 반복 횟수는 어느정도 조절해서 ms 단위에서 큰 숫자가 나오게만 조절하자
- 반복 횟수가 어느정도 많아졌다면 반복횟수 보다는 부하량을 조절하는 것이 옳다고 여겨진다.
- for 보다는 while이 더 빠르다.
- 정규식, indexOf 처럼 모든 요소에 대해서 검증을 해야하는 경우는 느리다.
- 재귀 함수는 느리다?
참조한 페이지
2진수 10진수 변환
[JS로 코테 준비하기] 10. 프로그래머스 - 이진수 더하기 (feat. 2진수 <-> 10진수)
