콜라문제

일반적으로 아는 문제이다.

그걸 더 일반화 시킨 문제이다.
나의 풀이
function sol0(a, b, n) {
let bottle = n
let newBottle = Math.floor(bottle/a)*b
let restBottle = bottle%a
let accumulateBottle = 0
bottle = restBottle + newBottle
accumulateBottle += newBottle
while ( bottle >= a) {
newBottle = Math.floor(bottle/a)*b
restBottle = bottle%a
bottle = restBottle + newBottle
accumulateBottle += newBottle
}
return accumulateBottle;
}만들다보니 반복문 밖에서 미리 한번 하고 들어간는데 문제없이 돌아간다.
다른 사람의 풀이
sol1 = (a, b, n) => Math.floor(Math.max(n - b, 0) / (a - b)) * ba가 b보다 커야지만 성립이 되는 코드다.
문제 조건에서도 그렇게 주어졌고, 상식적으로 안그럴 수 가 없다.
수학적으로 따지면 나는 한번에 최대한 교환을 한 것이고 이것은 한번에 최소값으로 교환을 한 것이다.
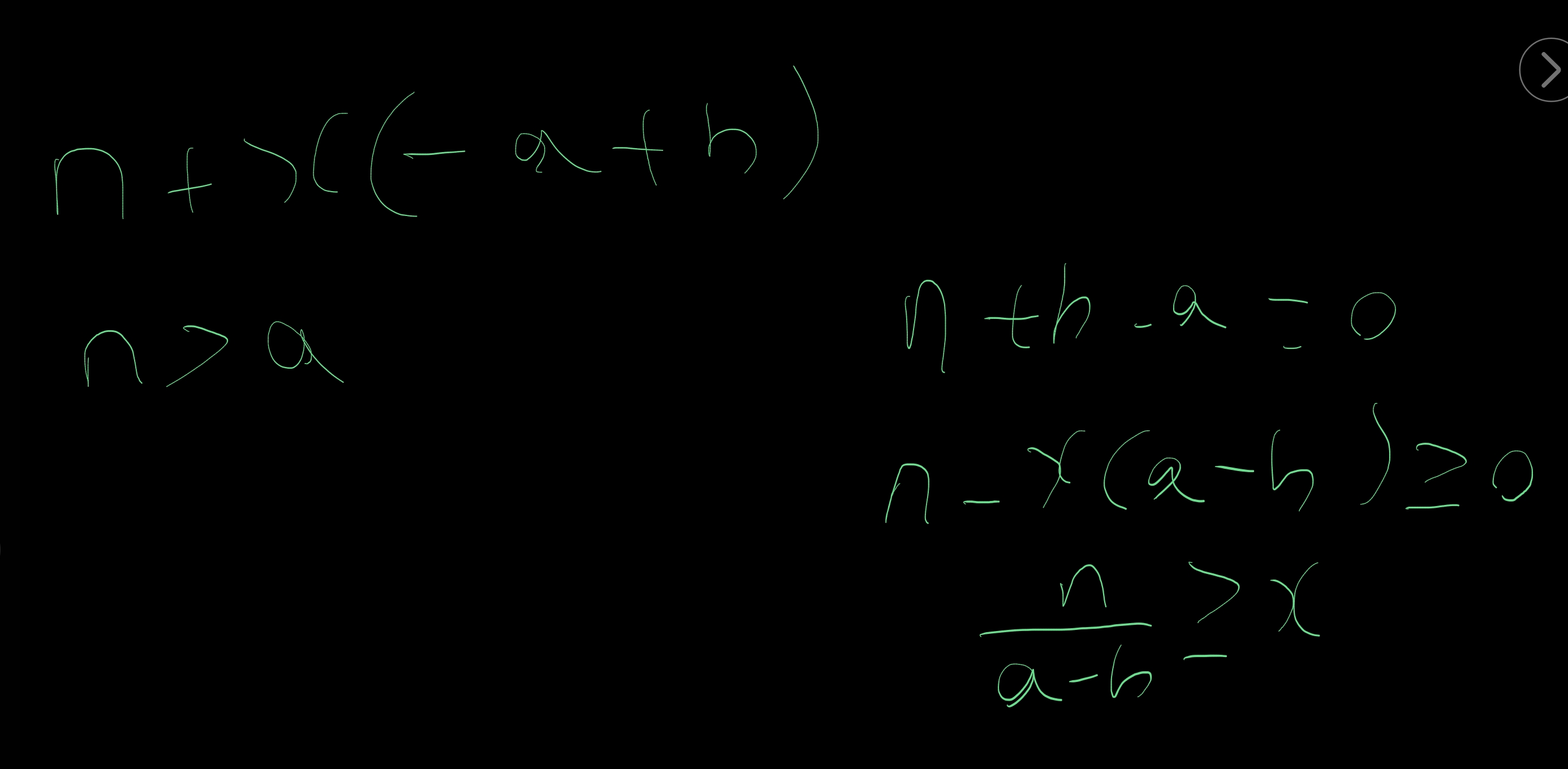
우리는 x번 교환할 수 있다.
그런데 그 x번을 어떻게 구하지?
바로 n + x ( -a + b ) >= 0 인 조건을 찾는것이다. 이쁘게 정리하면
그리고 이것을 부등호가 아니라 등호로 바꾸면
그런데 이대로 가버리면 값이 딱 맞을 수도 있지만 1더 크게 나올 수 도 있다.
왜냐하면 라서 교환이 불가능하지만 이어서 왠지 교환이 가능해 보이는 경우가 있을 수 있기 때문이다.
즉 n을 n-b로 바꾸고 소숫점 버림(Math.floor())처리를 할 필요가 있는 것이다.
Math.max로 음수일 경우에도 처리를 해놨는데 문제의조건 자체가 1 ≤ b < a ≤ n ≤ 1,000,000 이기 때문에 고려할 필요가 없다.
이던 시간복도가 로 획기적으로 줄었다. 수학은 신이야!

function sol02(a, b, n) {
var answer = 0;
let maxGiv = 0;
while(a<=n){
maxGiv = ~~(n/a)
answer += maxGiv*b
n = n-maxGiv*(a-b)
}
return answer;
} 짜리 답을 찾아냈으니 더이상 다른 걸 볼 필요가 없다. 하지만 Math.floor()대신 ~~라는 소수점 제거를 쓴게 신기해서 가져와봤다.
속도 비교
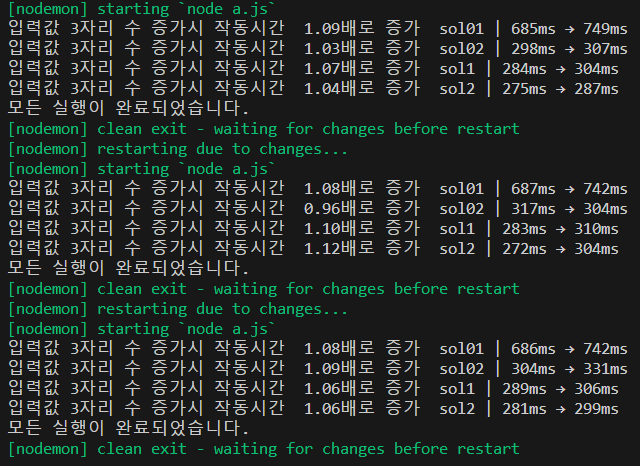
의외의 결과가 나왔다. sol01 > sol2 > sol1 = sol01 로 실행시간이 길것으로 예상했는데 실제로는
sol1 > sol02 > sol1 = sol2 였다.
sol01과 sol2는 시간복잡도가 같아서 당연히 비슷하게 나올줄 알았는데 아마도 반복문 안에서 얼마나 많은 일을 처리하느냐에 따라서 달라지는것같다.
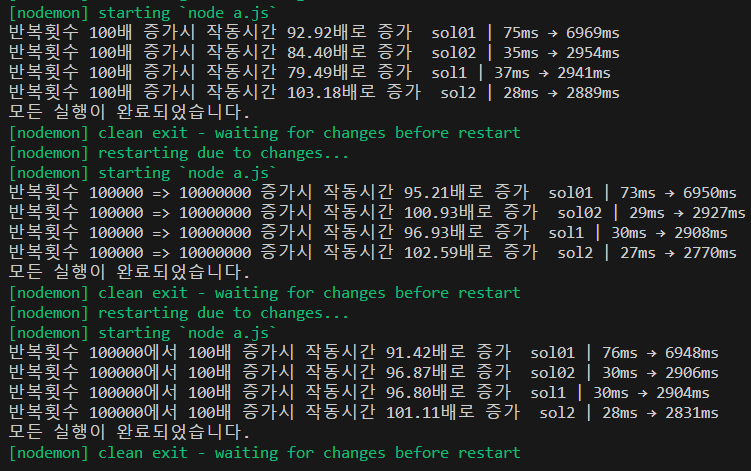
입력값 뿐 아니라 반복 횟수에서도 마찬가지다.
아무래도 시간복잡도가 최악의 경우를 가정하기 때문에 루프 횟수가 정직하게 줄어드는 경우에는 매우 큰 차이를 만들지 않는 것 같다.
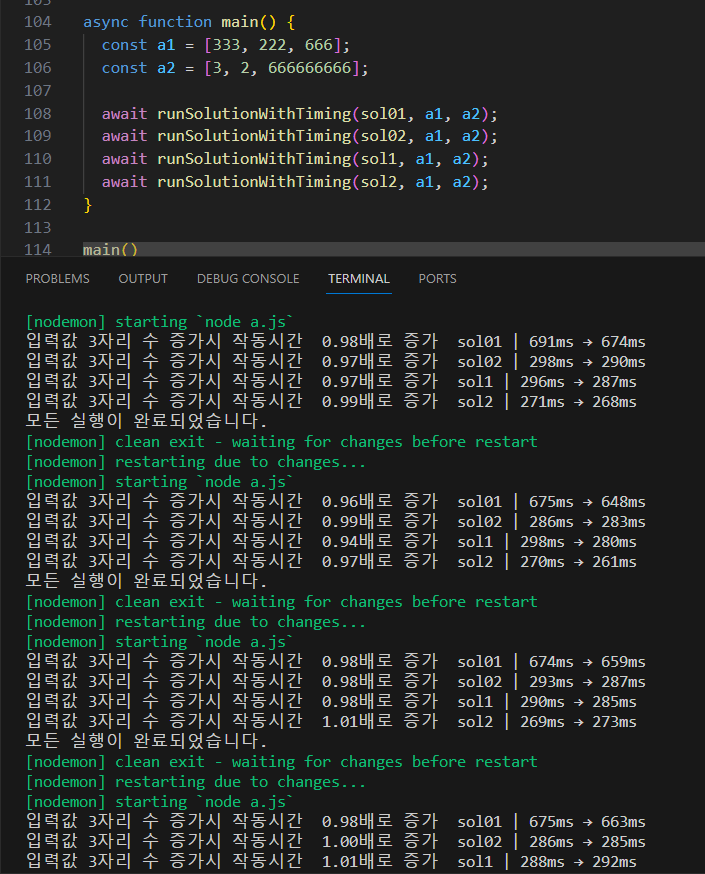
혹시나해서 n은 늘리고 a는 줄였는데도 이런다. 혹시 다른 것들도 시간복잡도가 이였던걸까?
피보나치 수

나의 풀이
function solution(n) {
var answer = 0;
let i = 2
let F = [0,1]
while (i <= n) {
F[i] = (F[i-2] + F[i-1]) %1234567
i++
}
answer = F[n]%1234567
return answer;
}실수로 안밖에 다 %1234567 을 넣었는데 결과적으로 엄청 빨라졌다.
문제에서 요구하는 것이 피보나치 수가 아니라 피보나치 수를 %1234567로 나누고 남은 값인 이유는 더 빠르게 연산하고 정수의 오버플로우를 피하기 위해서이다.
그럼 %1234567을 넣을 곳이 두군데 있으니까 네개의 바리에이션이 나오겠다.
sol00 : 어디에도 나누지않음
sol01 : 밖에서 나눔
sol10 : 안에서 나눔
sol11 : 양쪽 다에서 나눔
속도 비교
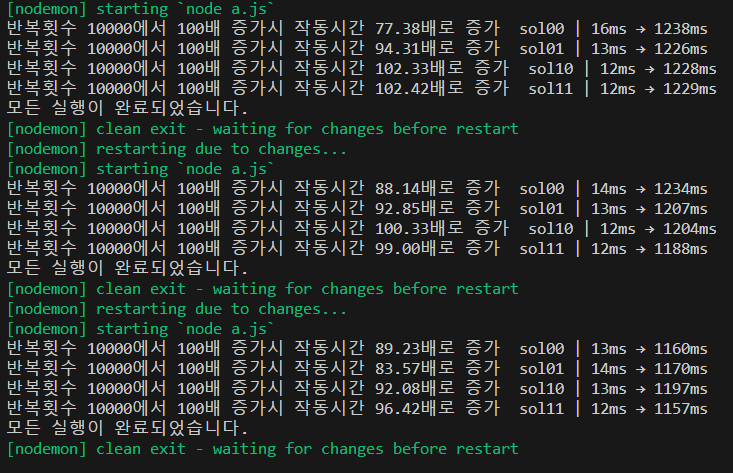
시간복잡도가 이므로 반복 횟수에 대해서는 정직하게 증가한다.
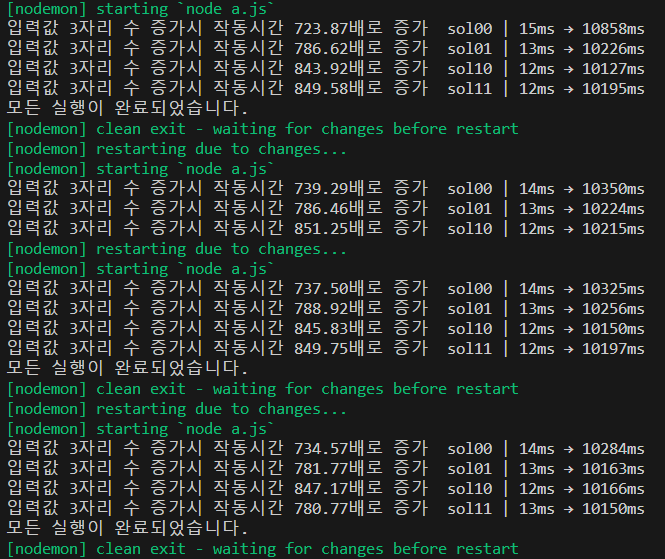
사실상 같은 코드이기 때문에 겨우 100만회 반복에 5자리수 정도 입력으로는 차이가 없는듯하다.
그래도 입력값이 클 때에는 sol00이 제일 느린듯하다.
공부하며 느낀 점
- 시간 복잡도도 중요하지만 입력값과 반복횟수가 그리 크지 않을때는 큰 영향을 주지 못한다.
