상관분석이란?
- 두 연속형 변수 간의 선형적 관계를 분석하는 기법
- 선형적인 관계 정도를 나타내기 위해 상관계수 사용
- 예를 들어, A변수가 증가함에 따라 B변수가 증가 or 감소되는지 분석하는 것
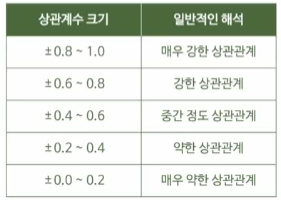
(+)일 수록 강한 상관관계인 게 아니라!!!
절대값일 수록 강한 상관관계를 가짐!!!
피어슨 상관계수
- 두 변수의 선형 관계를 측정
- 값을 -1에서 1사이로 반환, 1은 완벽한 양의 선형관계, -1은 완벽한 음의 선형관계
상관계수를 p라고 했을 때, 선형관계를 보여주는 예시들
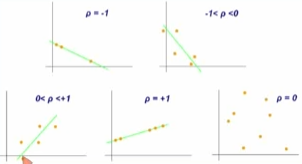
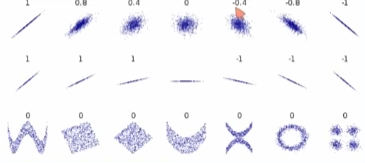
아래 그림에서 볼 수 있듯, 절대값이 높을수록 선 형태를 띔. 0인 경우에는 아예 비선형인 형태를 띔.
회귀 분석
회귀 분석에는 단순선형회귀(X와 Y가 각각 1개임)와 다중선형회귀(X가 여러개임)가 있음
선형 회귀(Linear Regression)란?
- 데이터를 가장 잘 설명할 수 있는 선을 찾는 분석 방법
- b1(회귀 계수)와 b0로 데이터의 원인과 결과 간의 선형 관계를 설명함
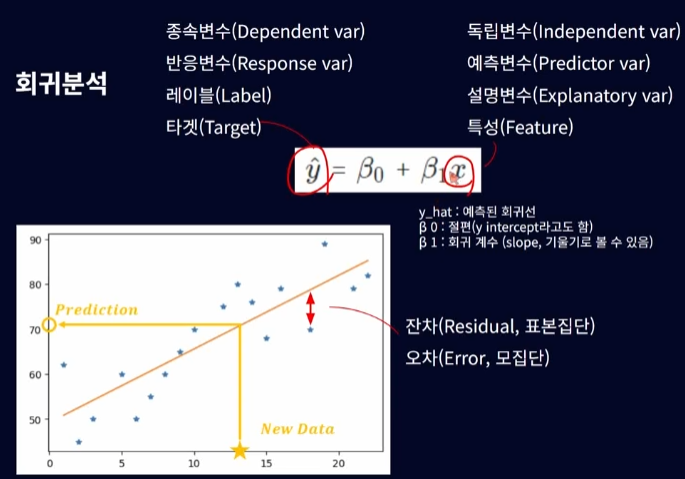
목표:
- 회귀 문제의 목표는 독립 변수(X)와 종속 변수(Y) 간의 관계를 모델링하여, 주어진 독립 변수에 대한 종속 변수의 값을 예측하는 것
원리:
- 선형 회귀는 독립 변수<->종속 변수 간의 선형 방정식을 찾아내는 방법으로,
- 주어진 데이터를 가장 잘 설명하는 최적의 회귀 계수를 찾고, 이를 통해 새로운 독립 변수 값에 대한 종속 변수 값을 예측할 수 있음
- 즉, X와 Y간의 선형 방정식을 가장 잘 대표하는 회귀 계수를 찾고, 이 회귀 계수로 다른 독립 변수의 결과도 예측 가능하다는 말
평가 지표:
- MSE(평균 제곱 오차):
예측값과 실제값의 차이를 제곱하여 평균한 값 (작을 수록 정확함) - R^2(R-squared):
종속 변수의 변동성 중, 모델이 설명할 수 있는 변동성의 비율 (1에 가까울 수록 정확함)
값이 0.25정도여도 유의미하다고 판단하며, 현업에서도 0.3 이상인 경우를 찾기 힘들다고 함 - MAPE(펑균 절대 비율 오차):
예측값이 실제값에 비해 얼마나 차이가 나는지를 %로 표현
대표 알고리즘:
선형 회귀, 다항 회귀, 릿지 회귀, 라쏘 회귀, 엘라스틱넷 ...
🔵 흥미로웠던 점:
'선형 회귀 분석' 이라는 단어를 보기만 했을 때는 무슨 의미인지 확 와닿지 않았는데, 그림과 함께 시각적으로 학습하니 일단 무슨 개념인지 단번에 이해할 수 있었다!
🔵 다음 학습 계획:
머신러닝의 기초에 대해 배울 예정입니다.
