데이터의 종류
수치형 데이터 (Numerical)
정의:
- 수치값으로 표현 가능한 데이터
- 연속적 또는 이산적
예시:
- 연속적인 경우 = 키, 몸무게, 온도 등
- 이산적인 경우 = 판매된 제품의 개수, 사람 수 등
분석방법:
- 중앙값, 평균, 표준편차 등의 통계적 수치를 통해 분석 가능함
- 시각화 방법으로 히스토그램, 산점도 그래프 등이 있음
범주형 데이터 (Categorical)
정의:
- 명확하게 분류 및 라벨링할 수 있는 데이터
예시:
- 순서가 있는 경우 = 학력 수준 등
- 순서가 없는 경우 = 국적, 성별, 색상, 카테고리 등
분석방법:
- 평균이나 표준편차같은 통계는 X
- 각 카테고리의 빈도나 비율을 통해 분석
- 시각화 방법으로 바 차트, 파이 차트, 스택 차트 등이 있음
데이터의 종류를 알아야 하는 이유
분석기법
- 데이터의 유형에 따라 분석 방법이 다르기 때문
- 수치형은 회귀분석이 가능하지만, 범주형은 다른 방법이 필요함
전처리
- 데이터를 분석하기 전, 필요한 전처리 과정이 다름
- NA값(빈 값) 처리도 수치형/범주형에 따라 방법이 달라짐, 범주형 데이터에 대한 인코딩 등..
시각화
- 데이터 유형에 따라 시각화 방법이 달라짐
- 수치형은 박스플롯 등, 범주형은 바/파이 차트 등...
지표(metric) 란??
- 모든 수치는 지표, 즉 metric이 될 수 있음. 그래서 지표가 무슨 역할을 하냐면
- 특정 현상이나 변화가 관측됐을 때, 지표를 관찰함으로서 해당 상황의 핵심을 파악할 수 있게 해줌
- 예를 들어, 사람들은 소비자물가지수를 확인함으로써 물가가 높아지는 상황/낮아지는 상황에 대응함
증감률(%) 과 퍼센티지 포인트(%p)의 차이
증감률(%):
정의:
이전 기간 대비 현재 기간의 값이 얼마나 변화했는지 나타내는 비율

예시:
지난달 매출이 10만원, 이번 달 매출이 11만원일 경우, 매출의 증가율은 10% 임
퍼센티지 포인트(%p):
정의:
퍼센트의 증감을 나타내는 단위로,
퍼센트 자체의 변화를 나타낼 때 사용함
예시:
지난해 시장점유율은 30%, 올해 시장점유율은 35%일 때, 시장점유율이 5%p 상승했다고 할 수 있음
그 외 지표 :
광고 - CTR, ROAS, Cost per Acquisition ...
운영 - DAU, Clicks, Time spent, Retention ...
마케팅 - CAC, NPS, CLTV, Shares ...
재무 - ROI, CAGR ...
(분석을 하는 도메인에 알맞게 지표를 설정해주어야 합니다.)
기술통계량 (Descriptive statistics)
기술통계량이 왜 필요할까?
기술통계량을 통해 데이터의 특징(중심 경향성, 퍼짐/형태/위치의 척도)을 빠르게 파악하고, 분석의 방향성을 결정할 수 있다고 합니다.
(예를 들어, A 제품의 월별 판매 데이터가 있을 때, 기술통계량을 사용하여 판매 추세/이상치/판매량의 변동 등을 빠르게 파악할 수 있음)
중심 경향성을 나타내는 지표:
평균:
- 말그대로 자료 전체의 평균(=경향)을 나타냄
- 단점: 극단적인 값(Outlier)에 영향을 받음
중앙값(Median):
- 크기순으로 정렬한 데이터에서 중앙에 위치한 값(정렬된 순서가 가운데인)
- 장점: 이상치에 영향을 받지 않음
- 단점: 자료의 수가 많아지면, 대표성이 사라짐
최빈값(Mode):
- 가장 빈도가 많은 값
- 장점: 숫자로 나타내지 못하는 자료의 경우에도 구할 수 있음
- 단점: 자료의 개수가 적은 경우, 자료 전체의 특징을 반영하지 못 할 수 있음. 빈도가 모두 동일한 경우, 중복이 발생할 수 있음
퍼짐을 나타내는 지표:
범위:
- 변동성을 파악하기 위한 가장 쉬운 방법
- 장점: 간단히 계산 가능
- 단점: 범위만 알 수 있어서, 데이터가 그 안에 어떻게 퍼져있는지는 알기 어려움
분산(Variance):
- 데이터가 중심(평균)으로부터 얼마나 멀리 떨어져있는지를 계산
- 장점: 자료가 평균에서 얼마나 흩어져 있는지에 대한 대표값
- 단점: 제곱을 해서 계산하므로, 수치가 직관적이지는 않음 (분산값만 봐선, 그래서 얼마나 떨어져있다는 건지 바로 파악하기 어려움)
표준편차(standard deviation):
- 분산에 루트를 씌워, 자료의 단위와 동일하게 표현한 값
- 장점: 자료의 단위와 동일하기 때문에, 직관적으로 해석할 수 있음
형태를 나타내는 지표:
왜도(skewness):
- 데이터의 비대칭도. 왼쪽/오른쪽으로 치우친 정도
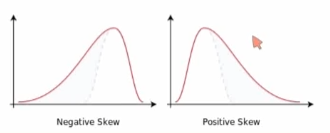
첨도(kurtosis):
- 데이터의 뾰족함. 높은 값은 더 많은 꼬리+뾰족한 분포를 의미함
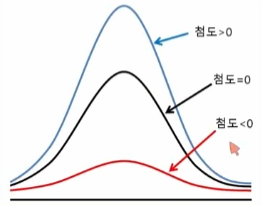
왜도와 첨도가 극단적이면 모델이 학습하기 어렵다고 함. 예를 들어서 첨도가 너무 낮으면 특징을 잡아내기 어렵다고 함.
즉, 데이터를 다듬어서 모델이 잘 학습할 수 있도록 하는 것이 최종 목표!
위치를 나타내는 지표:
백분위수(Percentile):
- 전체 데이터 중, 특정 백분율이 위치하는 값
(예 : 키 백분위수 95%야! = 상위 5%야)
4분위수(Quartile):
- 전체 관측값을 작은 순서로 배열한 후, 4등분하는 값
- 25%, 50%, 75%에 위치한 값 = 제1사분위수(Q1), 제2사분위수(Q2), 제3사분위수(Q3)
정규분포와 정규성 검증
정규분포를 알아야 하는 이유?
- 표본의 평균을 추정하거나, 두 집단 간의 차이를 검정할 때 '정규'분포가 사용됨
- 많은 통계적 기법들이 정규분포를 기반으로 함
중심극한정리 ?
- 큰 표본의 평균은 곧 정규분포에 가까워진다는 것을 의미하며, 이는 다양한 분석 상황에서 통계적 추론의 근거가 됨
- 즉, 많은 기법들이 정규분포를 기반으로 하는데에 반해 실제 데이터들은 정규분포를 완벽히 따르진 않음. 하지만 큰 표본의 평균은 정규분포에 가까워지므로, 통계적 기법을 기반으로 추론할 수 있는 근거가 됨
데이터 정규성 검증
- 많은 통계적 기법들은 정규분포를 따르기 때문에, 우리가 분석할 데이터가 정규분포를 따를 수 있는지 검증하는 것은 분석의 정확성을 확보하는데에 매우 중요함
범주형 데이터 분석 예제
이상탐지 및 데이터 정제:
- 정규분포를 이해하면 데이터셋 내 이상치를 식별하고 처리하는 데에 도움이 됨
- 특히 표준편차를 기반으로 한 이상치 탐지는 데이터 전처리 과정에서 핵심
기계학습 알고리즘의 적용:
- 많은 기계학습 알고리즘들은 데이터가 특정 분포를 따른다고 가정
- 이러한 가정을 이해하는 능력은 알고리즘의 선택과 성능 향상에 중요함 (내 데이터셋이 어떤 분포를 띄는지 알고, 해당 분포에 맞는 알고리즘 활용할 줄 알게됨)
실험 설계:
- A/B테스트 등 설계 시, 정규분포를 실험 결과 해석을 위한 기본적인 도구
표본의 개념과 표본평균의 의미
통계적 추론?
현실적으로 모든 모집단의 데이터를 수집하는 것은 어려운 일이므로, 특정 개수의 표본을 뽑아 모집단의 정보를 추측하는 과정
= 모집단을 몰라도, 표본평균을 이용해서 모집단의 평균을 예측할 수 있음
= 충분한 n(>30)을 여러 번 Sampling하면 모집단의 평균과 근접해지므로 모집단의 특성을 유추해볼 수 있음
정규성 검정(Normality test)?
정규성 검정이란, 특정 데이터셋이 정규분포를 따르는지 검증하는 과정, 필수적임
귀무가설(H0):
데이터셋이 정규분포를 따르는지 알아내는 가설
대립가설(H1):
귀무가설과 반대되는 가설, 즉 데이터셋이 정규분포를 따르지 않는지 알아내는 가설
정규성 검정 방법:
- 샤피로-윌크 검정
- 콜모고로프-스미르노프 검정
- 앤더슨-달링 검정
- QQ-Plot
데이터셋에 여러 방법을 적용해보고, 정규성을 검증하는 것이 좋습니다.
정규성을 띄지 않는다고 해서 분석을 못 하는 것은 아니고, 정규성을 띄도록 데이터를 변환한 후 통계적 방법론을 통해 분석하면 됩니다.
🔵 흥미로웠던 점:
중간에 도메인별 통계 지표에 대해 간략하게 적어두었는데, 각 지표가 무엇을 의미하는지 간단하게라도 알아두어야 실제 분석할 때 유용하게 써먹을 수 있겠다고 생각했다. 오늘치 학습이 끝나고 찾아봐야겠다.
🔵 다음 학습 계획:
데이터의 관계를 파악하기 위한 기초분석 중, 상관관계와 회귀분석에 대해 배울 것입니다.
