벡터란?
- 벡터는 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성요소
- 벡터는 크기와 방향을 가짐
- 벡터와 달리 크기만을 갖는 값은 스칼라(Scalar)라고 함
- 공학에서는 보통 벡터 공간 = 유클리드 공간. 따라서, 유클리드 벡터/기하 벡터/공간 벡터 라고도 부름
- 점 A에서 점 B까지의 벡터는 아래 그림처럼 나타냄
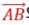
벡터의 기본적인 성질
동등성 :
- 벡터는 크기와 방향만을 가지므로, 원점의 특정한 위치는 아무런 의미를 갖지 않음
- 즉, 원점이 일치하지 않더라도, 두 화살표의 방향과 크기가 일치하면 동일한 벡터임
영 벡터 :
- 영 벡터는 크기가 0인 벡터를 의미함
음 벡터 :
- 자신(벡터)에게 더했을 때 결과가 영 벡터가 되는 벡터는 음 벡터라고 함
- 즉, 크기는 같지만 방향이 반대인 벡터
- a라는 벡터의 음벡터는 -a
벡터의 성분, 분해, 합성
벡터의 분해?
- 한 벡터를 자신의 성분 벡터들의 합으로 나타내는 것을 의미함
성분 벡터란?
- 벡터를 각각의 좌표축에 투영시킨 벡터를 성분 벡터라고 함
- 2차원 이상의 공간에서는 차원의 수 만큼 성분이 존재함
- a= ax+ay로 표현 가능함
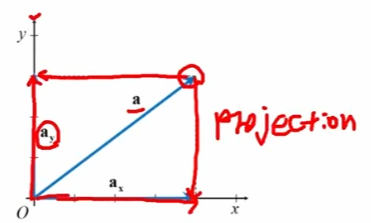
아래 그림의 경우, 벡터 a를 y축에 투영시킨 ay와 x축에 투영시킨 ax가 있음.
이때, ay와 ax는 벡터 a의 성분 벡터가 됨
단위 벡터
-
단위 벡터란 크기가 1인 벡터를 의미함
-
이는 벡터의 방향을 나타내기 위할 뿐, 차원과 단위가 없음
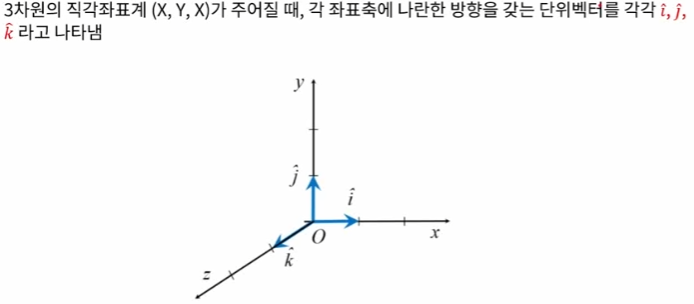
-
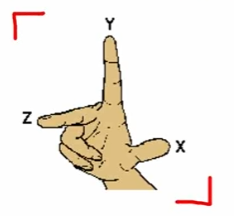
축의 방향은 '오른 나사 규칙'을 따름
-
모든 좌표축(x,y,z)에 대한 단위 벡터들의 집합 {i,j,k}을 기저벡터 집합(basis vectos) 라고 부름
-
따라서, "성분 벡터 = 스칼라와 단위 벡터의 곱" 으로 나타낼 수 있음

벡터의 연산 (덧셈과 뺄셈)
벡터의 덧셈 방법 : (1) 삼각형법
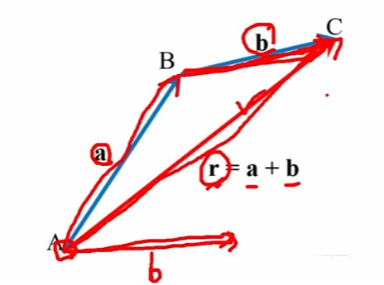
벡터의 덧셈 방법 : (2) 평행사변형법
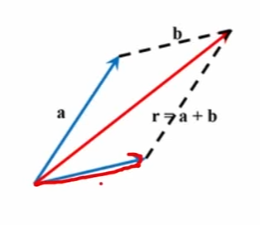
- B를 평행 이동하여, a와 b의 꼬리를 일치시킵니다.
- 두 벡터를 인접한 두 변으로 하는 평행 사변형을 그립니다.
- 두 벡터의 꼬리에서 시작하는 평행 사변형의 대각선이 a와 b의 합벡터에 해당합니다.
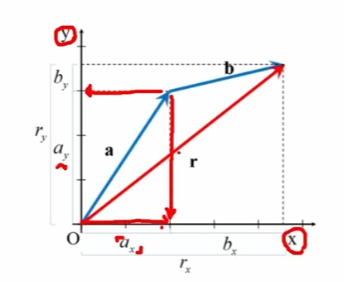
벡터의 덧셈 방법 : (3) 성분
두 벡터의 성분 벡터를 같은 축끼리 더해주는 방법입니다.
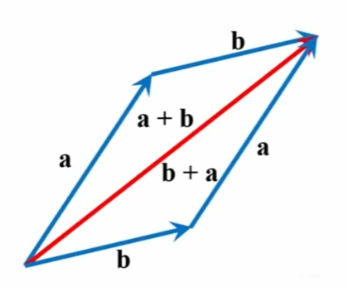
벡터의 덧셈 : 교환 법칙
벡터의 덧셈은 교환법칙을 만족합니다. 즉, 두 벡터의 순서가 바뀌어도 결과는 동일합니다.
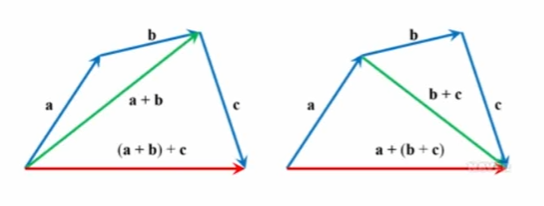
벡터의 덧셈 : 결합 법칙
벡터의 덧셈은 결합 법칙도 만족합니다. 더하는 벡터의 수가 2개 이상인 경우에도, 순서에 상관 없이 결과는 동일합니다.
벡터의 뺄셈 방법
자기 자신과 크기는 같고, 방향이 정반대인 음벡터의 정의를 이용하면 됩니다.
(즉, 음벡터를 '덧셈'해준다고 생각하면 될 듯)
벡터의 연산 (내적과 외적)

벡터의 내적
- 내적은 벡터를 수처럼 곱하는 개념
- 교환법칙, 결합법칙 O
- 각 벡터가 방향이 일치하는 정도만큼만 곱해짐
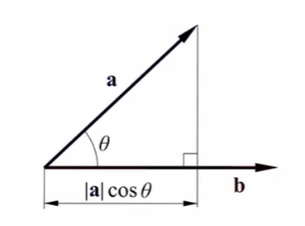
- 즉, 내적은 한 벡터를 다른 벡터로 투영시켜서, 투영된 벡터의 크기를 곱함
- 예를 들어, 두 벡터가 이루는 각이 90도이면, 한 벡터를 다른 벡터에 투영시키면 한 벡터는 무조건 영 벡터가 되므로 내적의 값은 0이 됨
- 따라서 내적의 결과는 크기값(Scalar)!
공식
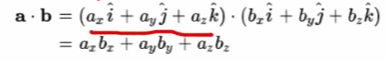
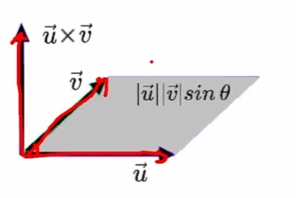
벡터의 외적
- 외적도 벡터를 곱하는 개념
- 교환법칙, 결합법칙 X
- 하지만 외적의 결과는 벡터!!
- 외적의 결과는 두 벡터 a와 b가 이루는 평면에 수직인 벡터
- 자기 자신과 곱한 결과는 0
공식
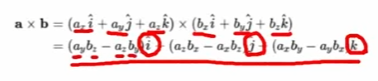
🔵 흥미로웠던 점 :
옛날에 학창 시절에 수학 공부를 할 땐 공식을 달달이 외웠던 것 같은데, 알고보니 내적이 '한 벡터를 다른 벡터에 투영시켰을 때, 그 투영 벡터와의 곱'으로 설명될 수 있다는 걸 알게 되었다. 이처럼 이전에는 그저 암기했던 개념들을 원리부터 이해할 수 있어서 재밌었다.
🔵 다음 학습 계획 :
행렬에 대해 배울 것입니다.
