행렬이란?
- 말 그대로 행(행 벡터)과 열(열 벡터) 로 이루어진 배열
- 행x열(mxn) 로 나타낼 수 있음
- 행은 가로로 가는 벡터라고 볼 수 있고, 열은 세로로 가는 벡터라고 볼 수 있다고 함
- 행렬을 이용하면 복잡한 자료를 쉽게 계산하고 이해할 수 있다고 함
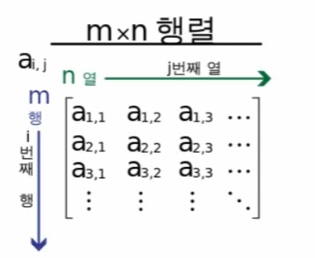
행렬의 성분
- 각 Amn을 A의 m번째 행 n번째 열의 성분(entry) 또는 원소(element) 또는 계수(coefficient) 라고 함
- Aii (i는 0~m 또는 0~n)를 대각 성분(diagonal entry) 또는 대각 원소(diagonal element) 또는 대각 요소 또는 주대각성 성분 이라고 함
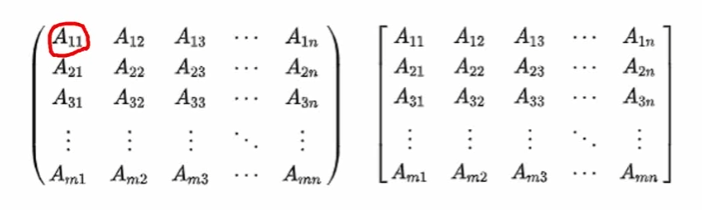
정방행렬 (= 정사각행렬, Square matrix)
- 행과 열의 수가 같은 행렬(m=n)
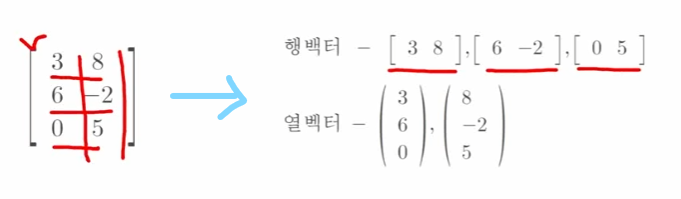
행 벡터, 열 벡터?
- 만약 m=1이라면, 행렬 A는 1xn인 행 벡터(Row vector)라고 함
- 만약 n=1이라면, 행렬 A는 mx1인 열 벡터(Column vector)라고 함
행렬의 계산
행렬의 덧셈 뺄셈
- 위치가 같은 원소들끼리 더해주면 됨
- 단, 행렬의 크기가 동일해야 함!
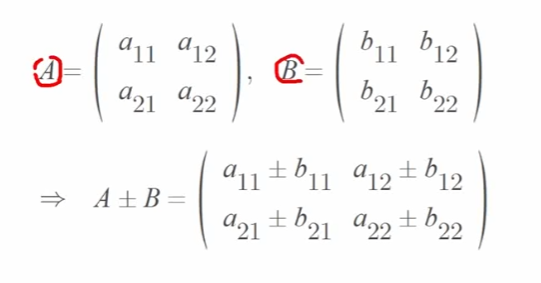
행렬의 곱셈 : 상수곱
- 행렬 A와 상수 k의 곱셈은 행렬 A의 각 성분에 k를 곱해주면 됨
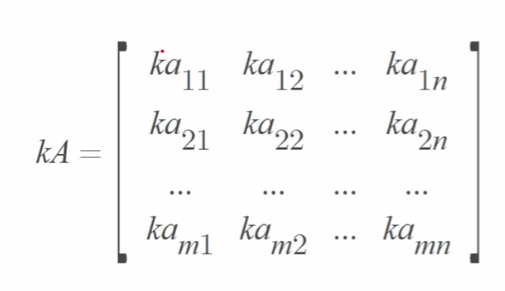
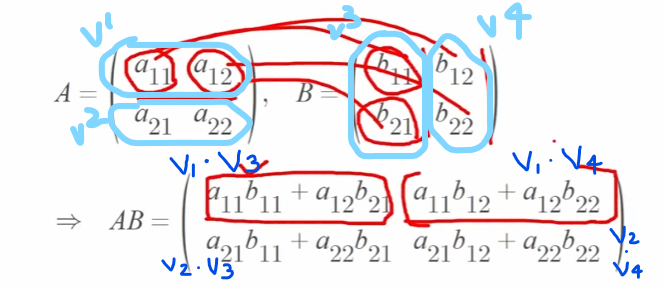
행렬의 곱셈 : 행렬끼리의 곱
-
행렬의 곱셈은 앞 행렬의 열 갯수와 뒷 행렬의 행의 수가 같을 때만 가능함
-
아래 그림에서 볼 수 있듯, 행렬의 곱셈은 벡터의 내적과 비슷함
(= 앞 행렬의 행벡터와 뒷 행렬의 열벡터와의 내적)
-
앞 행렬의 크기가 mxn이고, 뒤 행렬의 크기가 nxk이면 두 행렬을 곱한 결과의 크기는 mxk
-
행렬의 곱셈은 교환법칙 성립 X
전치 행렬
- 전치 행렬이란 행렬을 뒤집어 놓은 형태



역행렬
- 역행렬이란, 자신에게 곱했을 때 단위 행렬(대각 성분이 모두 1이고 나머지는 0)이 되는 행렬
- 사이즈가 클 경우 계산 비용 매우 증가
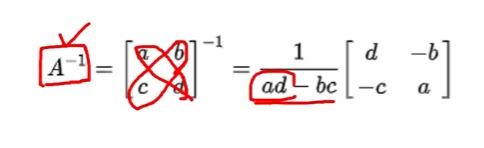
기타 특수 행렬
단위 행렬
- 대각 성분이 1이고, 나머지는 0인 행렬!
- 단위 벡터처럼, 행렬의 사이즈(행,열) 를 알려줌

대각 행렬
- 대각 성분 외의 값이 모두 0인 행렬

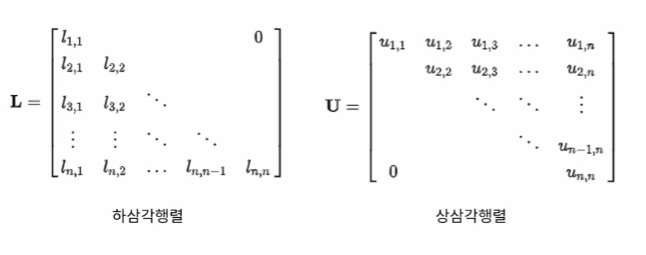
삼각 행렬
- 상관계수 표 시각화할 때, 중복되는 부분 masking으로 제거할 때 쓰임
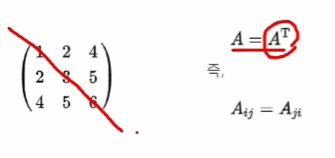
대칭 행렬
- 대각선을 기준으로 값이 대칭인 행렬
- 자신의 Transpose와 동일
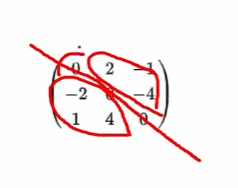
반대칭 행렬
- 대각선을 기준으로 부호만 다르고, 절대값은 대칭인 행렬
- 즉, 행렬 A의 Transpose = -행렬 A
🔵 흥미로웠던 점:
행렬을 벡터로 생각하니, 행렬의 곱셈이 아주 직관적으로 이해되었다!
🔵 다음 학습 계획:
선형대수학의 기본 개념부터 배울 예정입니다.
