대칭 행렬 이란?
행렬 A가 있다고 할 때,
- 정사각행렬 이면서
- A의 Transpose = A
를 만족하는 행렬
즉, 대칭 행렬은 항상 대각화가 가능하고, 이 대각화 과정으로 복잡한 행렬을 더 간단한 형태로 변환해 문제를 해결하는 데 유용합니다.
대각화 복습
- 고유벡터는 선형적으로 독립적임
- P는 column이 고유벡터로 이루어진 행렬, D는 대각성분이 고유값으로 이루어진 행렬
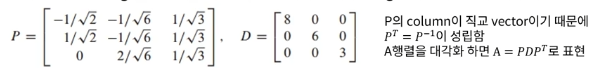
직교 기저?
직교 기저는 공간의 모든 벡터가 서로 직각(90도)으로 이루어진 기저를 말합니다. 예를 들어, 2차원 공간에서의 직교 기저는 (1,0)과 (0,1)과 같은 벡터 쌍입니다.
-
대칭 행렬 A가 다음과 같다고 할 때,
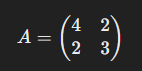
-
행렬 A의 고유 값을 구하기 위해 다음 식을 사용합니다.
det(A−𝜆I)=0
이를 계산하면 고유 값이
𝜆1=5와 𝜆2=2로 나오고, 고유 벡터를 각각 구해보면

가 됩니다.
-
고유벡터 v1과 v2가 직교하는지 확인합니다.
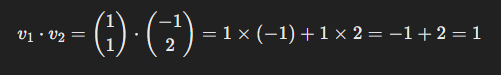
두 벡터를 내적한 값이 0이 아니므로, 직교하지 않음을 알 수 있습니다. -
직교하지 않으면, 벡터들을 정규화하여 직교 기저를 구합니다.
직교 기저가 왜 필요할까???
아래와 같이 직교 기저를 구했다고 가정했을 때,

직교 기저와 고유값을 가지고 P와 D를 구성할 수 있고,
P와D를 가지고 행렬 A를 A=PxD의 형태로 대각화할 수 있습니다.
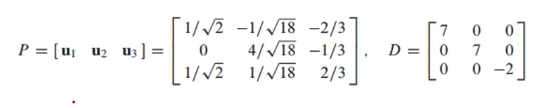
스펙트럼
행렬 A의 고유값 집합을 A의 스펙트럼이라고 부릅니다.
A가 대칭 행렬이라면, 다음과 같은 성질을 따릅니다.
- A가 n개의 고유값을 갖고 있으면, multiplicity를 계산할 수 있음
- 각 고유값에 해당하는 고유공간의 차원은 고유값의 multiplicity와 동일함
- 고유공간은 서로 직교함. (따라서 서로 다른 고유공간에 존재하는 고유벡터들도 직교함)
다음 포스팅에 이어서...
