대각화
아래 그림처럼, 대각 행렬의 제곱은 대각 성분의 제곱이므로, 연산이 매우 간단해짐!
즉, 대각화는 연산을 단순하게 해주는 데 목적이 있다고 할 수 있습니다.
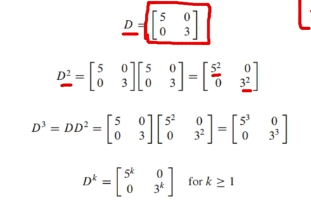
이 말은 즉슨,
정사각행렬 A가 대각 행렬과 유사(similar)하다면 A를 대각화 가능(diagonalizable) 하다고 합니다.
A가 대각행렬(D)과 유사한지 판별하는 공식은 아래와 같습니다.
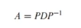
아래는 공식을 증명하는 과정입니다.

특징
- nxn 행렬 A가 대각화 가능하면, A는 대각행렬처럼 n개의 고유벡터를 가집니다.
- A=PDP(^-1)이면, P의 column은 A의 n개의 고유벡터들로 이루어집니다.
- D의 대각 성분은 P를 구성하는 각 고유벡터들에 대한 고유값, 즉 A의 고유값들이 됩니다.

대각화하기
(1) 행렬의 고유값 찾기

(2) 행렬의 고유벡터 찾기
각 고유값에 대해 고유 벡터들을 구합니다.

(3) 고유값으로 P를 구성하기
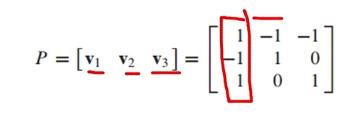
(4) 행렬 대각화하기
위에서 구한 고유값으로 행렬 D를 구성

대각화를 하는 이유
고유값과 고유벡터를 쉽게 구하기 위해서
고유값과 고유벡터를 구하는 이유
특정 행렬이 영향을 미치는 값과 그 벡터를 구하기 위해서...
다음 포스팅에 이어서...
