Reduced SVD 란?

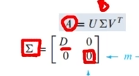
SVD시, 대각행렬 D는 대각 요소가 특이값으로 이루어진 행렬입니다.
즉, Σ에는 rxr크기의 행렬에만 특이값이 포함되어있고, r+1행과 r+1열부터는 값이 0입니다.

U와 V가 Σ와 곱해지면, r+1행과 r+1열부터는 0과 곱해져 무조건 0이 나오므로,
어차피 0이 나오는 것은 생략해버리자 라는 취지로 U와 V 행렬을 r까지만 표기한 것이 Reduced SVD의 개념입니다.

유사역행렬(Pseudo inverse) 이란?

유사역행렬은 A+라고 부르며, 최소제곱법을 구하는데 이용됩니다.
A+는 Reduced SVD의 전치(Transpose)입니다.

최소제곱법이란??
최소 제곱법의 목표는 각 데이터에 대해 모델이 예측한 값과 실제 값 사이 오차의 제곱합을 최소화하는 것입니다. 즉, 주어진 데이터에 대해 가장 잘 맞는 함수 또는 모델을 찾는 방법론이라고 할 수 있습니다.

---

🔵 흥미로웠던 점:
LU분해, 고유벡터와 고유값 까지는 어떻게든 이해하면서 넘어갈 수 있었는데
대각화와 특이값 분해에선 "그래서 이 개념이 실제로 어디에, 어떻게 쓰이는 거지?" 하는 생각이 계속 들었다. 아직 데이터 분석을 본격적으로 시작해보지 않아서 이런 의문이 생기는 것 같다. 실제로 분석을 해보면 와닿는 부분이 많겠지??... 그렇게 되도록 개념을 잘 숙지해두려고 한다.

🔵 다음 학습 계획:
기초 통계에 대해서 배우고, 시간 날 때 길버트의 선형대수 강의 영상을 짬짬이 보려고 한다.