---

1 결측치 탐색

---

1.1 결측치

• 데이터의 값이 누락된것 = 결측값, Missing Values
  • NA 또는 N/A(Not Applicable or Not Available), NaN(Not a Number), NULL로 표기됨
• 전산오류, 입력누락, 인위적 누락 등으로 발생함
• 설문조사(survey)와 종단연구(longitudinal research)에서 보편적으로 발생
  • 설문조사는 참가자 중 일부가 답변하기 곤란한 질문에 의도적으로 응답을 하지 않을 수 있음
  • 종단연구는 특정 대상을 장기간에 걸쳐 조사하는 것으로, 사망, 임의탈퇴, 연락두절 등의 상태가 발생

---

1.2 결측치의 유형

• MCAR(Missing Completely At Random, 완전 무작위 결측)
  • 결측치가 발생한 변수의 값에 상관없이 전체에 걸쳐 무작위로 발생한 경우
  • 통계적으로 결측치의 영향이 없으므로 제거 가능
• MAR(Missing At Random, 무작위 결측)
  • 결측치가 발생한 변수의 값이 다른 변수와 상관관계가 있어 추정이 가능한 경우
  • 통계적으로 결측치의 영향이 다소 있으나 편향은 없으므로 대체 가능함
• MNAR(Missing Not At Random, 비무작위 결측)
  • 결측치가 발생한 변수의 값과 관계가 있고 그 이유가 있는 경우
  • 통계적으로 결측치의 영향이 크므로 결측치의 원인에 대한 조사 후 대응이 필요함
    

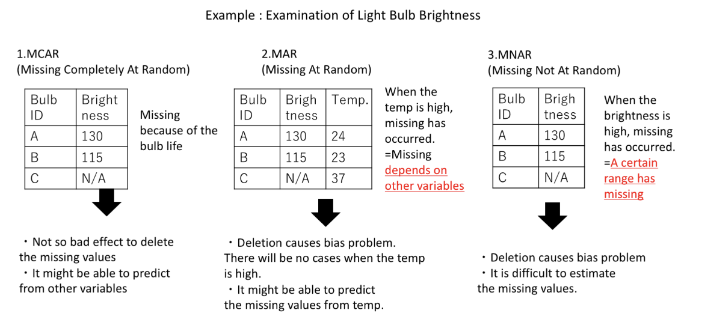
👉 결측치의 유형 예

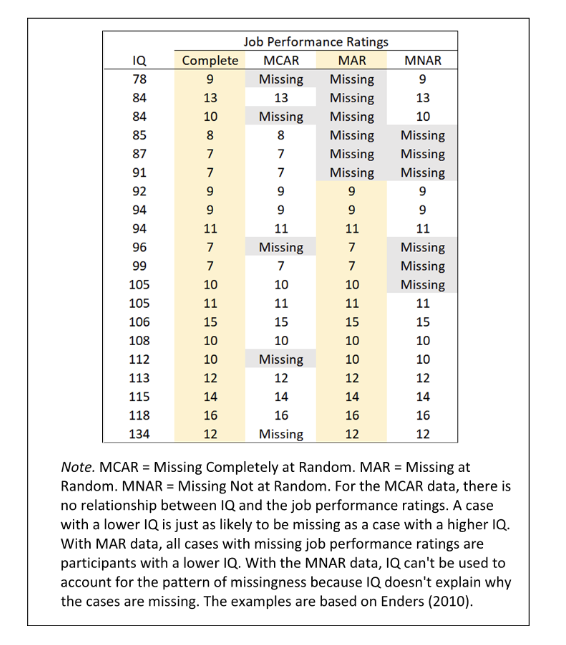
(위에서)

• MCAR은 특별한 패턴이 없이 데이터가 누락
• MAR은 낮은 IQ영역에서만 데이터 누락, IQ로 Job Performance Ratings를 어느정도 추정 가능
• MNAR은 패턴은 존재하나 IQ로 추정이 불가능

---

1.3 결측치 탐색

1.3-1 Pandas를 이용한 결측치 탐색

• (colab 기준) preprocessing_students.csv 를 다운로드 하여 content 파일에 업로드 해준다

import pandas as pd

# 데이터 세트 불러오기
df = pd.read_csv('preprocessing_students.csv', sep=',')
df.head()

👉 결과

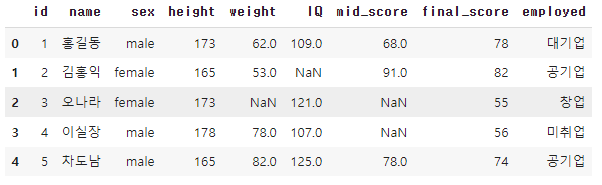
✍ 결측치 갯수 확인하기

• df.info(), df.isnull(), df.notnull(), sum(0), sum(1)

# 데이터 정보에서 Non-Null Count 갯수로 결측치 확인
df.info()

👉 결과

# isnull()의 True 개수를 합하여 확인 
print(df.isnull().sum(axis=0)) #  axis = 0 열기준, 1 행기준

👉 결과

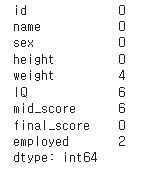
• 결측치는 weight, IQ, mid_score, employed로 각각 4,6,6,2개가 있음 (결측치의 유형은 파악 어려움)

1.3-2 klib을 이용한 결측치 탐색

pip install klib

import klib
import warnings

# 경고 메시지 무시
warnings.filterwarnings(action='ignore') 

# 결측치에 대한 프로파일링 플롯
klib.missingval_plot(df)

👉 결과

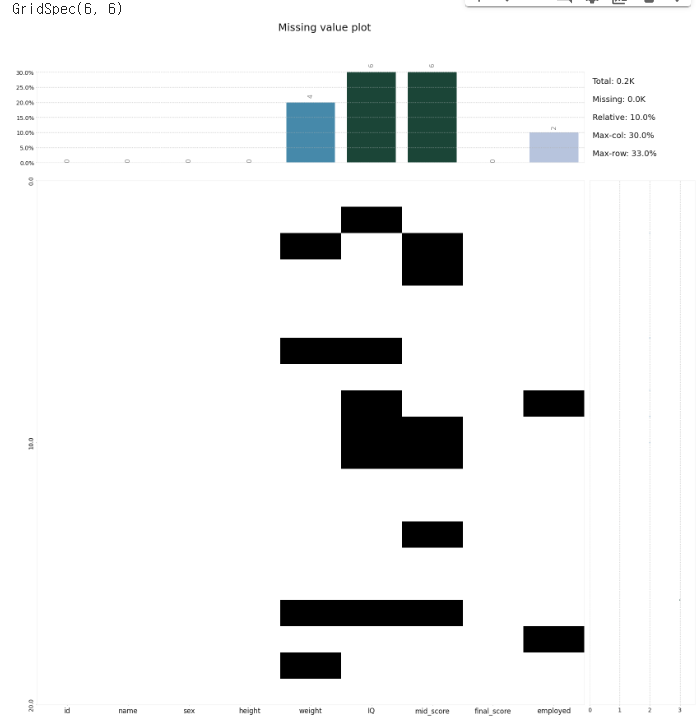
# 결측치에 대한 프로파일링 플롯
klib.missingval_plot(df, sort=True)

👉 결과

• 결측치 프로파일링 결과 weight, IQ, mid_score에 다수의 결측치가 존재

# 상관관계 플롯
klib.corr_plot(df) 

👉 결과

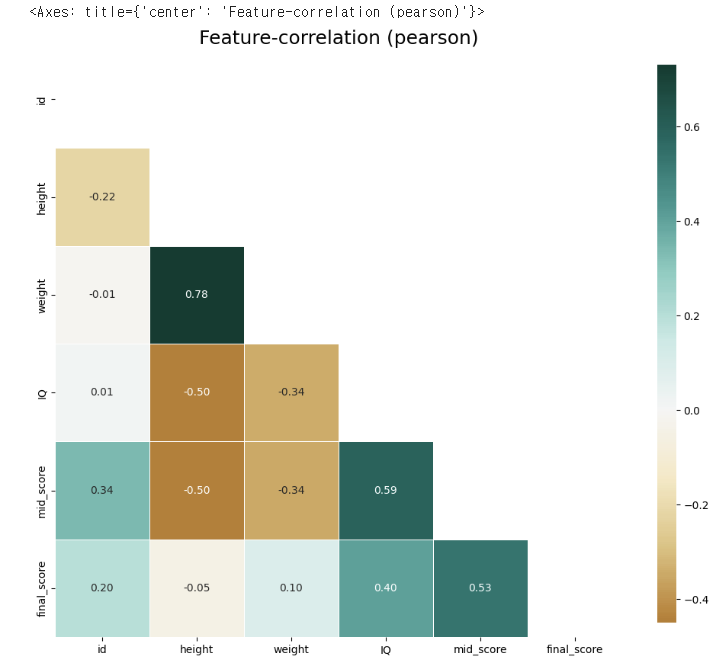
• 변수간 상관분석 결과 weight와 height의 상관관계가 강한 양의 상관관계(0.78), IQ와 mid_score가 양의 상관관계(0.59), mid_score와 final_score가 양의 상관관계(0.53)을 보이고 있음

import matplotlib.pyplot as plt
# 한글이 안나올 경우 폰트 지정
plt.rc('font', family='Malgun Gothic')

# 범주형 변수에 대한 분석
klib.cat_plot(df)

👉 결과

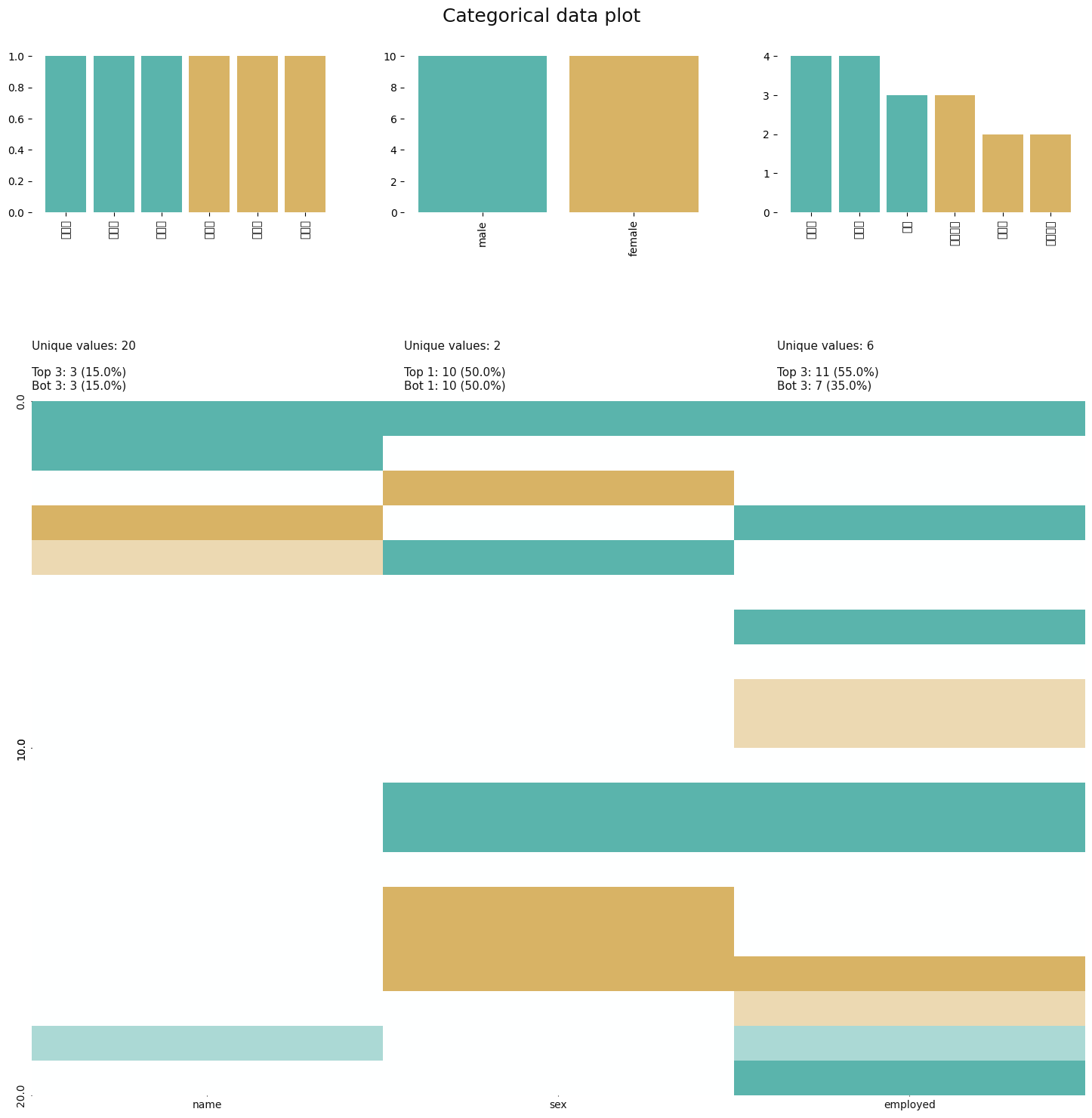
# 결측치가 있는 변수의 분포 확인
klib.dist_plot(df.weight)
klib.dist_plot(df.IQ)
klib.dist_plot(df.mid_score)

👉 결과

• weight는 특정한 패턴이 보이지 않음
• IQ는 중간 영역대의 밀도가 낮아 중간영역대의 데이터가 누락되었음을 확인 가능
• mid_score는 낮은 점수대의 데이터가 누락되었음을 확인 가능

---

2 결측치 처리

---

2.1 결측치 처리방법 개요

• 제거(deletion)
  • MCAR(완전 무작위 결측) 일때 사용 가능함
  • 데이터의 손실이 발생 -> 자유도 감소 -> 통계적 검정력 저하
  • 표본의 수가 충분하고 결측값이 10%-15% 이내일 때에는 결측값을 제거한 후 분석해도 결과에 크게 영향을 주지 않음
• 대체(imputation)
  • 표본 평균과 같은 대표값으로 대체할 경우 -> 대표값 데이터가 많아짐 -> 잔차 변동이 줄어듬 -> 잘못된 통계적 결론 유도
  • 모수추정 시 편향(bias) 발생함

---

2.2 결측치 제거(Deletion)

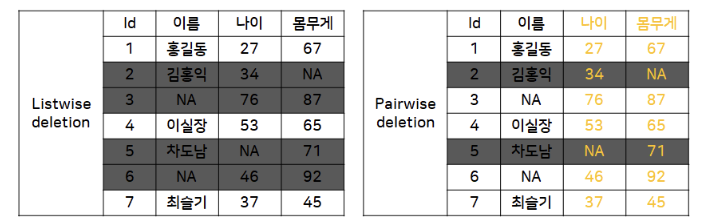
• 1. Listwise deletion
  • 결측치가 존재하는 행(instance) 자체를 삭제하는 방식
  • 데이터 표본의 숫자가 적은 경우 표본의 축소로 인한 검정력 감소
• 2. Pairwise deletion
  • 분석에 사용하는 속성의 결측치가 포함된 행만 제거하는 방식
  • MCAR일때만 가능함
    

import pandas as pd

# Listwise deletion
df_listwise = df.dropna()

# Pairwise deletion
df_pairwise = df.dropna(subset=['weight', 'mid_score'])

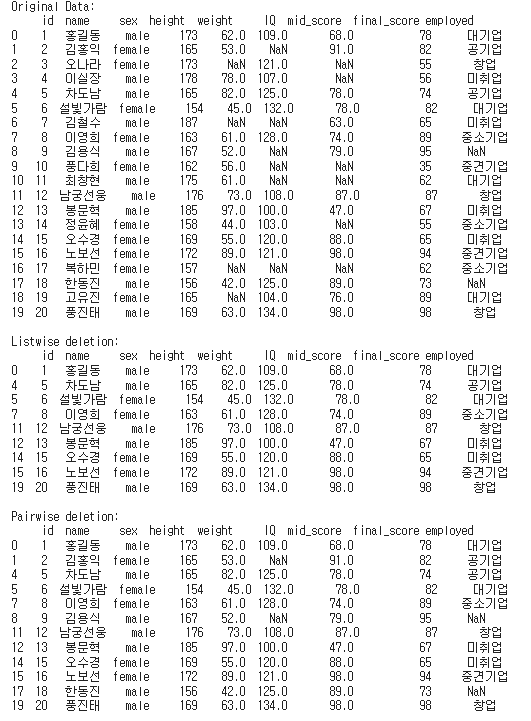
print(f'Original Data:\n {df}\n')
print(f'Listwise deletion:\n {df_listwise}\n')
print(f'Pairwise deletion:\n {df_pairwise}\n')

👉 결과

---

2.3 결측치 대체(Imputation)

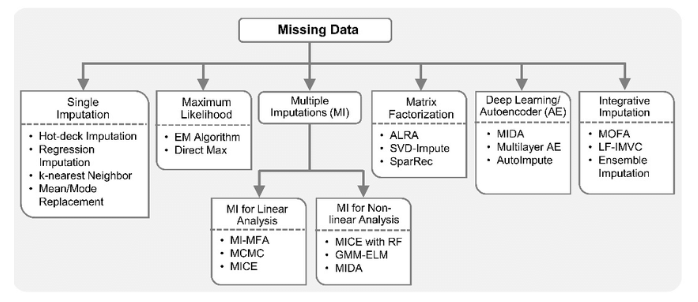
2.3-1 Single Imputation(단순대체법)

• 결측치의 대체값으로 하나의 값을 선정하는 것
• mean, correlation, 회귀계수와 같은 파라미터 추정시 편향(bias) 발생가능성 높음
• 이러한 추정 편향으로 인해 아예 결측값을 제거하는 것보다 통계적 특성이 나빠질 수 있음

📝 단순대체법 종류

• Explicit Modeling
• 1. Mean imputation
  • 데이터의 평균값(mean, median, mode)으로 결측값을 대체
  • 평균 대체 -> 표본오차 왜곡, 축소 -> 부정확한 p-value -> 검정력 약화
• 2. Regression imputation
  • 회귀식을 만들어 예측된 값으로 결측값 대체
  • 회귀 예측값 대체 -> 잔차 축소, 왜곡 -> R-squared 증가, 왜곡
• 3. Stochastic regression imputation
  • 회귀 예측값으로 대체하는 것과 유사하나, random error term을 추가하여 예측값에 변동을 주는 방법
  • 표본오차의 과소 추정 문제가 있음
• Implicit Modeling
• 1. Hot deck imputation
  • 연구중인 자료에서 표본을 바탕으로 비슷한 규칙을 찾아 결측값을 대체
  • 다른 변수에서 비슷한 값을 갖는 데이터 중에서 하나를 랜덤 샘플링하여 그 값을 복사
  • 결측값이 존재하는 변수가 가질 수 있는 값의 범위가 한정되어 있을때 사용
• 2. Cold deck imputation
  • 외부 출처에서 비슷한 연구를 찾아 결측값을 대체
  • Hot deck imputation과 유사하나, 어떠한 규칙 하(ex) k번째 샘플의 값을 취해오는 등..)에서 하나를 선정

2.3-2 단순대체법 Python 적용

• 1. Mean imputation
  • scikit-learn의 SimpleImputer 클래스를 사용
    • strategy : mean/mode/most_frequent
    • 데이터가 실수 연속값인 경우에는 평균 또는 중앙값을 사용, 값의 분포가 대칭적이면 평균이 좋고, 값의 분포가 심하게 비대칭인 경우에는 중앙값이 적당함
    • 데이터가 범주값이거나 정수값인 경우에는 최빈값을 사용함
• 2. Regression/Stochastic regression imputation
  • scikit-learn의 LinearRegression 사용
• 3. Hot deck/Cold deck imputation
  • Pandas의 fillna()적용

from sklearn.impute import SimpleImputer

df_imputed = pd.DataFrame.copy(df)

# 110대가 결측인 IQ는 평균으로 대체
df_imputed[['IQ']] = SimpleImputer(strategy="mean").fit_transform(df[['IQ']])

# 비대칭 분포를 갖는 mid_score는 중앙값으로 대체
df_imputed[['mid_score']] = SimpleImputer(strategy="median").fit_transform(df[['mid_score']])

# 범주형 employed는 Hot deck으로 대체
df_imputed['employed'].fillna(method='bfill', inplace=True) 

# height와 양의 상관관계가 있는 weight는 Stochastic regression으로 대체
from sklearn.linear_model import LinearRegression
import numpy as np
# 결측치가 있는 인덱스 검색
idx = df.weight.isnull() == True
# 학습을 위한 데이터 세트 분리
X_train, X_test, y_train = df[['height']][~idx], df[['height']][idx], df[['weight']][~idx]
# 선형회귀모형 인스탄스 생성 후 학습
lm = LinearRegression().fit(X_train, y_train)
# 예측값 + 변동값하여 결측치를 대체
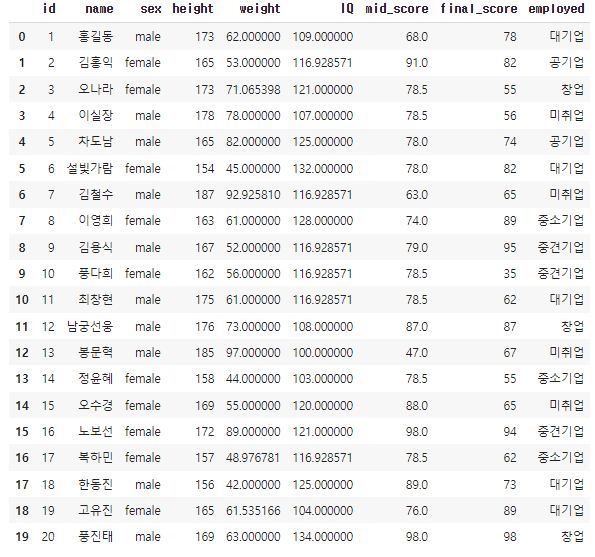
df_imputed.loc[idx, 'weight'] = lm.predict(X_test) + 5*np.random.rand(4,1)

df_imputed

👉 결과

2.3-3 다중대체법(Multiple Imputation)

• 결측치의 대체값을 여러 추정값을 종합하여 선정하는 것
• Multiple Imputation 3단계
  • 1. Imputation Phase: 가능한 대체 값의 분포에서 추출된 서로 다른 값으로 복수의 데이터 셋을 생성
  • 2. Analysis Phase: 각 데이터 셋에 대하여 모수의 추정치와 표본오차 계산
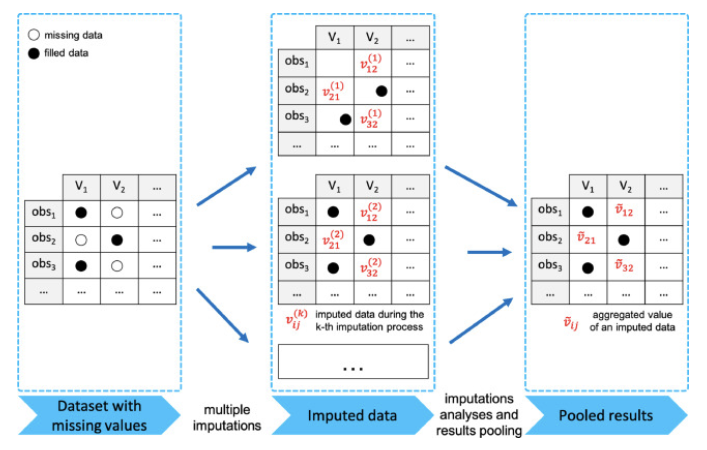
  • 3. Pooling Phase: 모든 데이터 셋의 추정치와 표본오차를 통합하여 하나의 대치값 생성
       

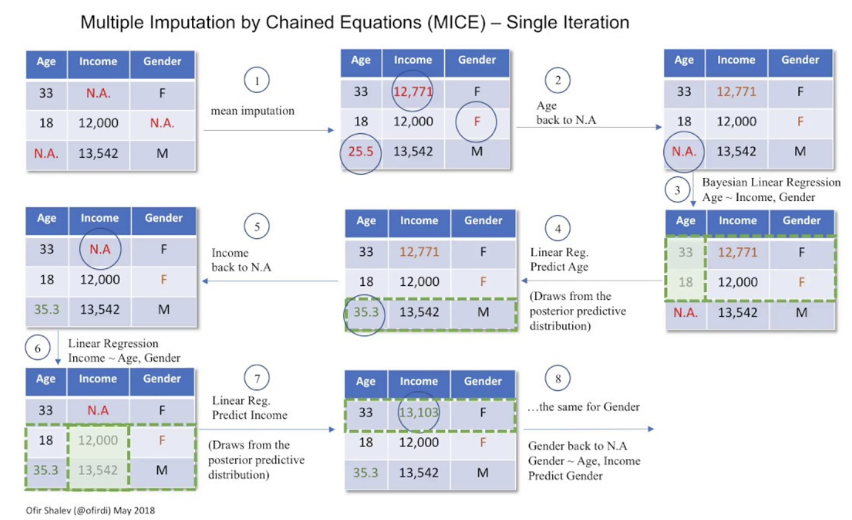
✍ MICE(Multiple Imputation by Chained Equations)

• 다중대체법의 한 종류
  

import numpy as np
# scikit-learn에서 R의 MICE 패키지를 따라서 실험적으로 개발 중
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

# 데이터 세트
X_train = [[33, np.nan, .153], [18, 12000, np.nan], [np.nan, 13542, .125]]
X_test = [[45, 10300, np.nan], [np.nan, 13430, .273], [15, np.nan, .165]]

# mice 인스탄스 생성
mice = IterativeImputer(max_iter=10, random_state=0)
mice.fit(X_train)

np.set_printoptions(precision=5, suppress=True)
print('X_train MICE: \n', mice.transform(X_train))
print('X_test MICE: \n', mice.transform(X_test))

👉 결과

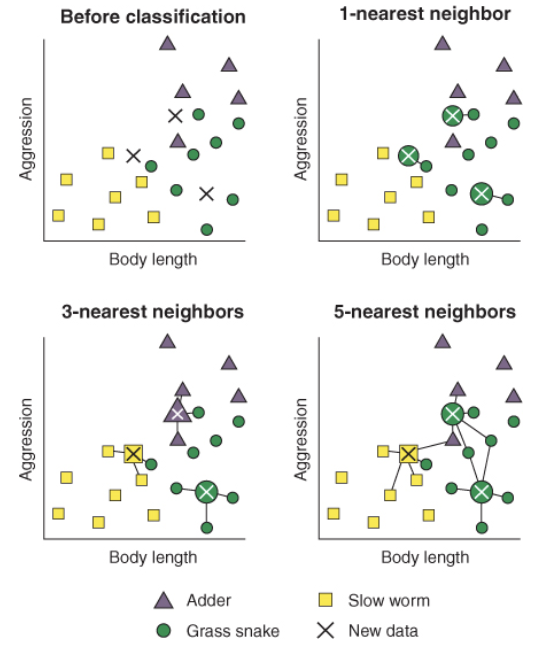
✍ KNN Imputation

• KNN(K-Nearest Neighbor)은 분석대상을 중심으로 가장 가까운 k개 요소(이웃)들 중에서 가장 많은 수의 집단으로 분류하는 지도학습 알고리즘
• KNN Imputation은 결측치가 범주형이면 이웃 데이터 중 최빈값으로 대체하고 연속형이면 이웃 데이터들의 중앙값으로 대체하는 방법
  

import numpy as np
from sklearn.impute import KNNImputer

knn = KNNImputer(n_neighbors=2, weights="uniform")
knn.fit(X_train)

print('X_train KNN: \n', knn.transform(X_train))
print('X_test KNN: \n', knn.transform(X_test))

👉 결과