1 피쳐엔지니어링
1.1 피쳐(feature)
- 데이터 모델(특히, 인공지능)에서 예측을 수행하는 데 사용되는 입력변수를 의미
- 통계학에서는 독립 변수라고 함
피쳐의 유형
- 속성에 따라
- 범주형(categorical): 범주나 순위가 있는 변수
- 수치형(numerical): 수치로 표현되는 변수
- 인과관계에 따라
- 독립변수(independent variable): 다른 변수에 영향을 받지 않고 종속변수에 영향을 주는 변수
- 종속변수(dependent variable): 독립 변수로부터 영향을 받는 변수
- 머신러닝에서
- 입력(input): 변수(Feature), 속성(Attribute), 예측변수(Predictor), 차원(Dimension), 관측치(Observation), 독립변수(Independent Variable)
- 출력(output): 라벨(Label), 클래스(Class), 목푯값(Target), 반응(Response), 종속변수(Dependent Variable)
1.2 피쳐 엔지니어링(Feature Engineering)
- 머신러닝 알고리즘의 성능을 향상시키기 위하여 데이터에 대한 도메인 지식을 활용하여 변수를 조합하거나 새로운 변수를 만드는 과정
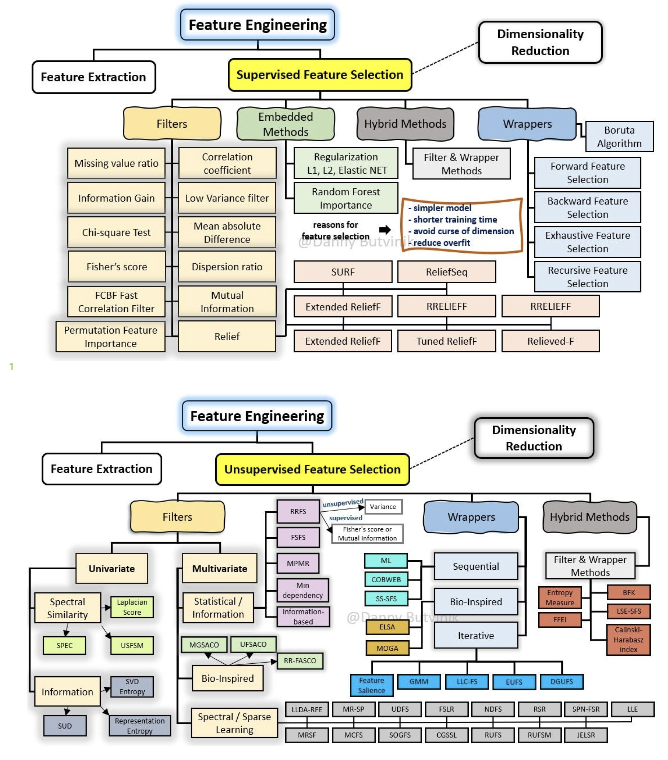
피쳐 추출(feature extraction)
- 피쳐들 사이에 내재한 특성이나 관계를 분석하여 이들을 잘 표현할 수 있는 새로운 선형 혹은 비선형 결합 변수를 만들어 데이터를 줄이는 방법
- 고차원의 원본 피쳐 공간을 저차원의 새로운 피쳐 공간으로 투영
- PCA(주성분 분석), LDA(선형 판별 분석) 등
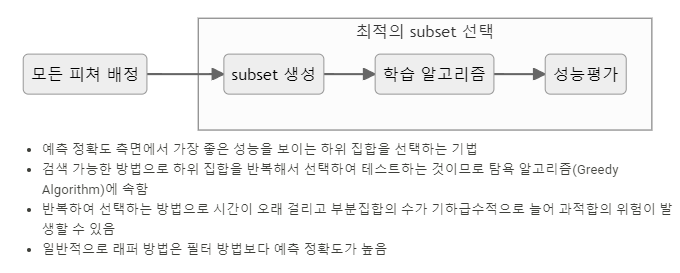
피쳐 선택(feature selection)
- 피쳐 중 타겟에 가장 관련성이 높은 피쳐만을 선정하여 피쳐의 수를 줄이는 방법
- 관련없거나 중복되는 피쳐들을 필터링하고 간결한 subset을 생성
- 모델 단순화, 훈련 시간 축소, 차원의 저주 방지, 과적합(Over-fitting)을 줄여 일반화해주는 장점이 있음
- Filter, Wrapper, Embedded 메서드
머신러닝 성능 향상을 위한 방법
- 피쳐 엔지니어링 적용
- 머신러닝 알고리즘의 하이퍼 파라미터를 최적화
2 피쳐 추출
2.1 피쳐 추출 (Feature Extraction)
-
변수들 사이에 내재한 특성이나 관계를 분석하여 이들을 잘 표현할 수 있는 새로운 선형 혹은 비선형 결합 변수를 만들어 데이터를 줄이는 방법
-
주성분 분석(Principal Component Analysis, PCA)
- 변수들의 공분산 행렬이나 상관행렬을 이용
- 원래 데이터 특징을 잘 설명해주는 성분을 추출하기 이하여 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
- 행의 수와 열의 수가 같은 정방행렬에서만 사용
-
선형판별분석(Linear Discriminant Analysis, LDA)
- 데이터의 Target값 클래스끼리 최대한 분리할 수 있는 축을 찾음
- 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화하는 방식으로 차원을 축소
-
특이값 분해(Singular Value Decomposition)
- M X N 차원의 행렬데이터에서 특이값을 추출하고 이를 통해 주어진 데이터 세트를 효과적으로 축약할 수 있는 기법
-
요인분석(Factor Analysis)
- 데이터 안에 관찰할 수 있는 잠재적인 변수(Latent Variable)가 존재한다고 가정
- 모형을 세운 뒤 관찰 가능한 데이터를 이용하여 해당 잠재 요인을 도출하고 데이터 안의 구조를 해석하는 기법
- 주로 사회과학이나 설문 조사 등에서 많이 활용
-
독립성분분석(Independent Component Analysis)
- 주성분 분석과는 달리 다변량의 신호를 통계적으로 독립적인 하부성분으로 분리하여 차원을 축소하는 기법
- 독립 성분의 분포는 비정규 분포를 따르게 되는 차원축소 기법
-
다차원 척도법(Multi-Dimensional Scaling)
- 개체들 사이의 유사성, 비유사성을 측정하여 2차원 또는 3차원 공간상에 점으로 표현하여 개체들 사이의 집단화를 시각적으로 표현하는 분석 방법
2.2 주성분 분석
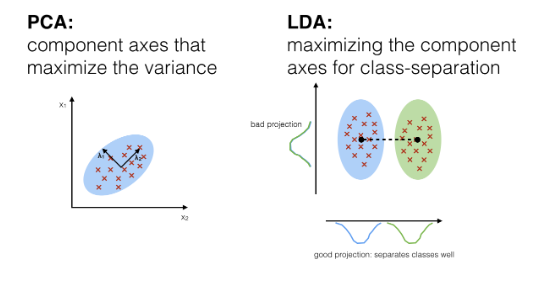
주성분 분석 (Principal Component Analysis)
- 가장 널리 사용되는 차원(변수) 축소 기법 중 하나
- 원 데이터의 분산(variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
- PCA는 기존의 변수를 조합하여 서로 연관성이 없는 새로운 변수, 즉 주성분(principal component, PC)들을 만들어 냄
- 주성분의 개수를 증가시킴에 따라 원 데이터의 분산의 보존수준이 높아짐
PCA 절차
- 학습 데이터셋에서 분산이 최대인 축(axis)을 찾음
- 첫번째 축과 직교(orthogonal)하면서 분산이 최대인 두 번째 축을 찾음
- 첫 번째 축과 두 번째 축에 직교하고 분산을 최대한 보존하는 세 번째 축을 찾음
- 1~3과 같은 방법으로 데이터셋의 차원(특성 수)만큼의 축을 찾음

2.3 선형판별분석
선형판별분석(Linear Discriminant Analysis, LDA)
- 입력 데이터 세트를 저차원 공간으로 투영(projection)해 차원을 축소하는 기법
- 데이터의 Target값 클래스끼리 최대한 분리할 수 있는 축을 찾음 → 지도 학습
- PCA는 Target값을 사용하지 않으므로 비지도 학습
LDA 절차
- 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화하는 방식으로 차원을 축소
- SVM 같은 다른 분류 알고리즘을 적용하기 전에 차원을 축소시키는 데 사용
2.4 Scikit-Learn으로 PCA와 LDA 수행하기
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# iris 데이터셋을 로드
iris = datasets.load_iris()
X = iris.data # iris 데이터셋의 피쳐들
y = iris.target # iris 데이터셋의 타겟
target_names = list(iris.target_names) # iris 데이터셋의 타겟 이름
print(f'{X.shape = }, {y.shape = }') # 150개 데이터, 4 features
print(f'{target_names = }') ↳ 결과
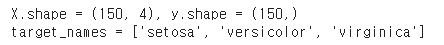
# PCA의 객체를 생성, 차원은 2차원으로 설정(현재는 4차원)
pca = PCA(n_components=2)
# PCA를 수행. PCA는 비지도 학습이므로 y값을 넣지 않음
pca_fitted = pca.fit(X)
print(f'{pca_fitted.components_ = }') # 주성분 벡터
print(f'{pca_fitted.explained_variance_ratio_ = }') # 주성분 벡터의 설명할 수 있는 분산 비율
X_pca = pca_fitted.transform(X) # 주성분 벡터로 데이터를 변환
print(f'{X_pca.shape = }') # 4차원 데이터가 2차원 데이터로 변환됨↳ 결과

# LDA의 객체를 생성. 차원은 2차원으로 설정(현재는 4차원)
lda = LinearDiscriminantAnalysis(n_components=2)
# LDA를 수행. LDA는 지도학습이므로 타겟값이 필요
lda_fitted = lda.fit(X, y)
print(f'{lda_fitted.coef_=}') # LDA의 계수
print(f'{lda_fitted.explained_variance_ratio_=}') # LDA의 분산에 대한 설명력
X_lda = lda_fitted.transform(X)
print(f'{X_lda.shape = }') # 4차원 데이터가 2차원 데이터로 변환됨↳ 결과

# 시각화 하기
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# Seaborn을 이용하기 위해 데이터프레임으로 변환
df_pca = pd.DataFrame(X_pca, columns=['PC1', 'PC2'])
df_lda = pd.DataFrame(X_lda, columns=['LD1', 'LD2'])
y = pd.Series(y).replace({0:'setosa', 1:'versicolor', 2:'virginica'})
# subplot으로 시각화
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
sns.scatterplot(df_pca, x='PC1', y='PC2', hue=y, style=y, ax=ax[0], palette='Set1')
ax[0].set_title('PCA of IRIS dataset')
sns.scatterplot(df_lda, x='LD1', y='LD2', hue=y, style=y, ax=ax[1], palette='Set1')
ax[1].set_title('LDA of IRIS dataset')
plt.show()↳ 결과

3 피쳐 선택 기법
- 종속변수 활용여부에 따라
- Supervised: 종속변수를 활용하여 선택
- Unsupervised: 독립변수들 만으로 선택
- 선택 메커니즘에 따라
- Filter: 통계적인 방법으로 선택
- Wrapper: 모델을 활용하여 선택
- Embedded: 모델 훈련 과정에서 자동으로 선택
- Hybrid: Filter + Wrapper
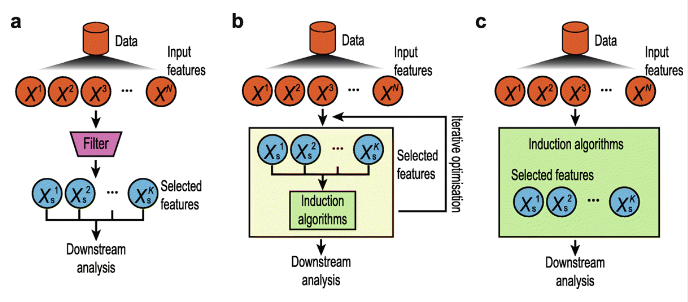
3.1 필터 기법(Filter Method)

필터기법의 종류
- 분산 기반 선택(Variance-based Selection)
- 분산이 낮은 변수를 제거하는 방법
- 정보 소득(Information Gain)
- 가장 정보 소득이 높은 속성을 선택하여 데이터를 더 잘 구분하게 되는 것
- 카이제곱 검정(Chi-Square Test)
- 카이제곱 분포에 기초한 통계적 방법으로 관찰된 빈도가 기대되는 빈도와 의미있게 다른지 여부를 검증하기 위해 사용되는 검증 방법
- 피셔 스코어(Fisher Score)
- 최대 가능성 방정식을 풀기 위해 통계에 사용되는 뉴턴(Newton)의 방법
- 상관계수(Correlation Coefficient)
- 두 변수 사이의 통계적 관계를 표현하기 위해 특정한 상관관계의 정도를 수치적으로 나타낸 계수
분산 기반 선택(Variance-based Selection)
from sklearn import datasets
from sklearn.feature_selection import VarianceThreshold
# iris 데이터셋을 로드
iris = datasets.load_iris()
X = iris.data # iris 데이터셋의 피쳐들
y = iris.target # iris 데이터셋의 타겟
X_names = iris.feature_names # iris 데이터셋의 피쳐 이름
y_names = iris.target_names # iris 데이터셋의 타겟 이름
# 분산이 0.2 이상인 피쳐들만 선택하도록 학습
sel = VarianceThreshold(threshold=0.2).fit(X)
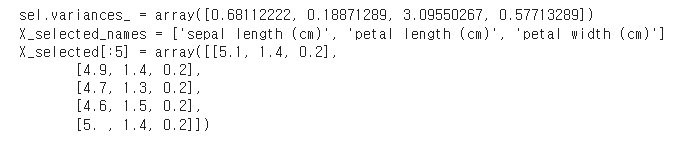
print(f'{sel.variances_ = }') # 각 피쳐의 분산 확인
# 분산이 0.2 이상인 피쳐들만 선택 적용
X_selected = sel.transform(X) # 분산이 0.2 이상인 피쳐들만 선택
X_selected_names = [X_names[i] for i in sel.get_support(indices=True)] # 선택된 피쳐들의 이름
print(f'{X_selected_names = }')
print(f'{X_selected[:5] = }')↳ 결과
Scikit-Learn 제공 피쳐 선택 메서드
- SelectKBest(): 고정된 k개의 피쳐 선택기
- SelectPercentile(): 분위수 기반 선택기
- SelectFpr(): False positive rate 기반 선택기
- SelectFdr(): 추정된 False discovery rate 기반 선택기
- SelectFwe(): familiy-wise error rate 기반 선택기
- GenericUnivariateSelect(): 단변량 피쳐 선택기
Scikit-Learn 제공 피쳐 선택 기준
- f_classif: ANOVA F-value 분류
- mutual_info_classif: 상호정보량(mutual information) 분류
- chi2: 카이제곱 분류
- f_regression: F-value 회귀
- mutual_info_regression: 상호정보량(mutual information) 회귀
F-value
- 두 모집단(확률변수)의 분산의 비율을 나타내는 값
- ANOVA, Regression에서는 모형이 설명하는 분산/잔차의 분산
- F-value가 크면 모형이 잘 설명하고 있다는 의미
상호정보량(mutual information)
- 하나의 확률변수가 다른 하나의 확률변수에 대해 제공하는 정보의 양
- 두 확률변수가 공유하는 엔트로피
- 두 확률변수가 독립이라면, 상호정보량은 0
- 두 확률변수의 상관관계가 강할수록 상호정보량이 커짐
χ2-test
- 범주형 데이터에서 두 요인간 독립성 검정에서 사용
- χ2-value가 크면 두 요인간 독립이 아니라는 의미(즉, 상관관계가 있음)
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif, f_regression, chi2
# k개의 베스트 피쳐를 선택
sel_fc = SelectKBest(f_classif, k=2).fit(X, y)
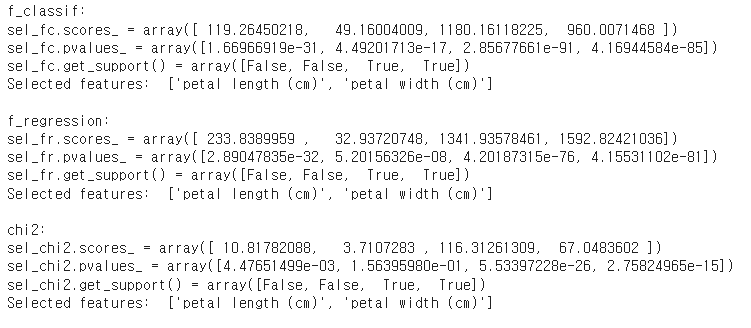
print('f_classif: ')
print(f'{sel_fc.scores_ = }')
print(f'{sel_fc.pvalues_ = }')
print(f'{sel_fc.get_support() = }')
print('Selected features: ', [X_names[i] for i in sel_fc.get_support(indices=True)]) # 선택된 피쳐들의 이름
sel_fr = SelectKBest(f_regression, k=2).fit(X, y)
print('\nf_regression: ')
print(f'{sel_fr.scores_ = }')
print(f'{sel_fr.pvalues_ = }')
print(f'{sel_fr.get_support() = }')
print('Selected features: ', [X_names[i] for i in sel_fr.get_support(indices=True)]) # 선택된 피쳐들의 이름
sel_chi2 = SelectKBest(chi2, k=2).fit(X, y)
print('\nchi2: ')
print(f'{sel_chi2.scores_ = }')
print(f'{sel_chi2.pvalues_ = }')
print(f'{sel_chi2.get_support() = }')
print('Selected features: ', [X_names[i] for i in sel_chi2.get_support(indices=True)]) # 선택된 피쳐들의 이름↳ 결과
3.2 래퍼 기법(Wrapper Method)
변수 선택을 위한 알고리즘
- 전진 선택법(Forward Selection)
- 모형을 가장 많이 향상시키는 변수를 하나씩 점진적으로 추가하는 방법
- 후진 제거법(Backward Elimination)
- 모두 포함된 상태에서 시작하여 가장 적은 영향을 주는 변수부터 하나씩 제거
- 단계적 방법(Stepwise Method)
- 전진선택과 후향제거의 결합
- 각 단계에서 최상의 속성을 선택하고 나머지 속성 중 최악의 속성을 제거하는 과정을 실행
- 의사결정트리
래퍼기법의 종류
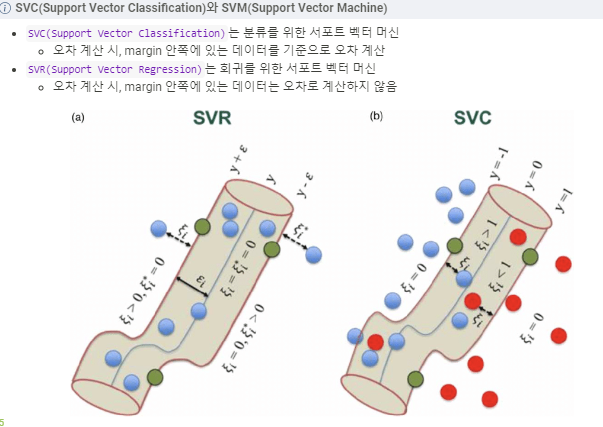
- RFE(Recursive Feature Elimination)
- SVM(Support Vector Machine)을 사용하여 재귀적으로 제거하는 방법
- 전진 선택, 후진 제거, 단계적 방법 사용
- SFS(Sequential Feature Selection)
- 그리디 알고리즘(Greedy Algorithm)으로 빈 부분 집합에서 특성 변수를 하나씩 추가하는 방법
- 전진 선택, 후진 제거 사용
# RFE(Recursive Feature Elimination) 적용
from sklearn.datasets import load_iris
from sklearn.feature_selection import RFE, RFECV, SelectFromModel, SequentialFeatureSelector
from sklearn.svm import SVC, SVR
# iris 데이터셋 로드
X, y = load_iris(return_X_y=True)
# 분류기 SVC 객체 생성, 선형분류, 3개의 클래스
svc = SVR(kernel="linear", C=3)
# RFE 객체 생성, 2개의 피쳐 선택, 1개씩 제거
rfe = RFE(estimator=svc, n_features_to_select=2, step=1)
# RFE+CV(Cross Validation), 5개의 폴드, 1개씩 제거
rfe_cv = RFECV(estimator=svc, step=1, cv=5)
# 데이터셋에 RFE 적용
rfe.fit(X, y)
print('RFE Rank: ', rfe.ranking_)
# rank가 1인 피쳐들만 선택
X_selected = rfe.transform(X)
X_selected_names = [X_names[i] for i in rfe.get_support(indices=True)] # 선택된 피쳐들의 이름
print(f'{X_selected_names = }')
print(f'{X_selected[:5] = }')
# 데이터셋에 RFECV 적용
rfe_cv.fit(X, y)
print('RFECV Rank: ', rfe_cv.ranking_)
# rank가 1인 피쳐들만 선택
X_selected = rfe_cv.transform(X)
X_selected_names = [X_names[i] for i in rfe_cv.get_support(indices=True)] # 선택된 피쳐들의 이름
print(f'{X_selected_names = }')
print(f'{X_selected[:5] = }')↳ 결과

# SFS(Sequential Feature Selector) : 순차적으로 특성을 선택하는 방법
from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
# 데이터를 로드하고, 분류기를 초기화한 후 SFS를 적용
X, y = load_iris(return_X_y=True)
knn = KNeighborsClassifier(n_neighbors=3)
sfs = SequentialFeatureSelector(knn, n_features_to_select=2, direction='backward')
# SFS를 학습하고, 선택된 특성을 출력
sfs.fit(X, y)
print('SFS selected: ', sfs.get_support())
# 선택된 피쳐들만 선택
X_selected = sfs.transform(X)
X_selected_names = [X_names[i] for i in sfs.get_support(indices=True)] # 선택된 피쳐들의 이름
print(f'{X_selected_names = }')
print(f'{X_selected[:5] = }')↳ 결과

3.3 임베디드 기법(Embedded Method)
임베디드 기법의 종류
- SelectFromModel
- 의사결정나무 기반 알고리즘에서 변수를 선택하는 기법
from sklearn.feature_selection import SelectFromModel
from sklearn import tree
from sklearn.datasets import load_iris
# 데이터를 로드하고, 분류기를 초기화한 후 SFS를 적용
X, y = load_iris(return_X_y=True)
clf = tree.DecisionTreeClassifier()
sfm = SelectFromModel(estimator=clf)
# 모형 구조 확인 및 출력을 pandas로 설정
sfm.set_output(transform='pandas')↳ 결과
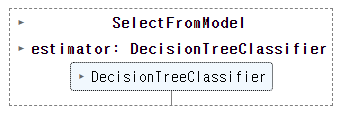
# 모형 학습
sfm.fit(X, y)
print('SFM threshold: ', sfm.threshold_)
# 선택된 피쳐들만 선택
X_selected = sfm.transform(X)
X_selected.columns = [X_names[i] for i in sfm.get_support(indices=True)] # 선택된 피쳐들의 이름
X_selected.head()↳ 결과
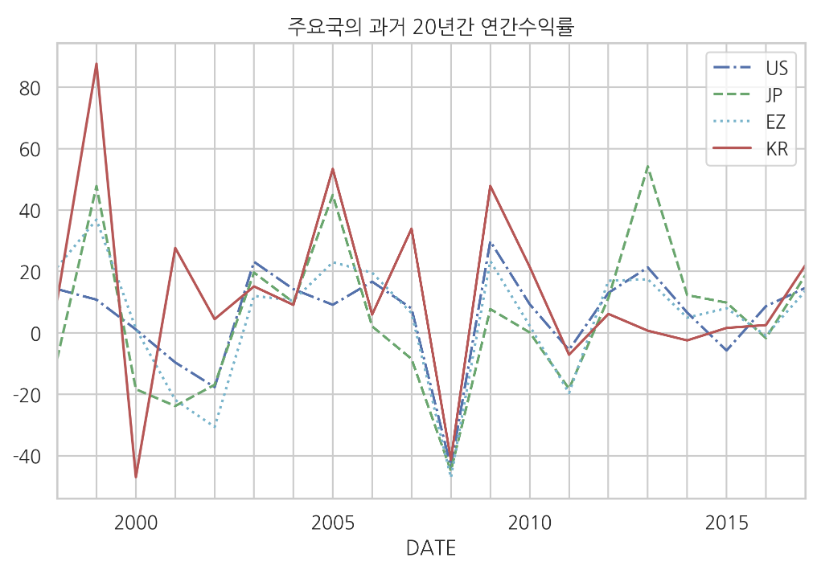
응용 사례
2.2 주성분 분석(PCA) 응용
PCA는 다양한 분야에서 사용된다. 주식이나 금융 분야에서도 PCA는 다양하게 쓰인다. 미국과 일본, 유럽, 한국의 과거 20년간의 주가를 살펴보는 예시에서 PCA가 사용된다.
pd.core.common.is_list_like = pd.api.types.is_list_like
import pandas_datareader.data as web
import datetime
symbols = [
"SPASTT01USM661N", # US: 미국
"SPASTT01JPM661N", # JP: 일본
"SPASTT01EZM661N", # EZ: 유럽
"SPASTT01KRM661N", # KR: 한국
]
data = pd.DataFrame()
for sym in symbols:
data[sym] = web.DataReader(sym, data_source='fred',
start=datetime.datetime(1998, 1, 1),
end=datetime.datetime(2017, 12, 31))[sym]
data.columns = ["US", "JP", "EZ", "KR"]
data = data / data.iloc[0] * 100
styles = ["b-.", "g--", "c:", "r-"]
data.plot(style=styles)
plt.title("세계 주요국의 20년간의 주가")
plt.show()↳ 결과
# 세계 주가의 공통요인은 평균값으로 구할수 있음
m = pca2.mean_
m↳ 결과

# 나라별로 주가를 다르게 하는 요인은 '주성분' 으로 구할 수 있음
p1 = pca2.components_[0]
p1↳ 결과