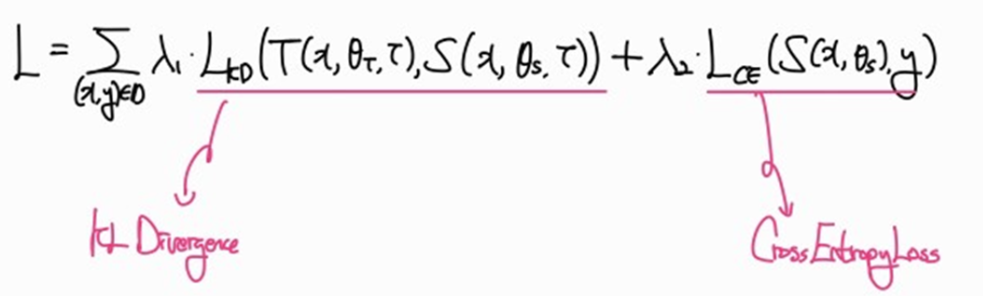Knowledge Distillation에 대한 고찰(feat. Cross Entropy)

https://arxiv.org/abs/1503.02531

Knowledge Distillation(지식증류)를 활용해서 모델 경량화를 진행하던 도중 한 가지 의문이 발생했고 한번 수식을 파고 들어봤다. 까먹기전에 블로그에 올려놔야겠다.

Knowledge Distillation의 수식을 살펴보면 KL Divergence와 CrossEntropyLoss로 구성되어있다. 하지만 CrossEntropy 또한 “예측분포와 실제분포 간의 손실”을 계산하는 것인데, 굳이 KL Divergence를 사용해야 하는 이유가 있을까? 라는 생각이 들었다. 이를 고찰하기 위해 먼저 KL Divergence와 CrossEntropy의 차이부터 알아보자.

즉, Cross Entropy Loss는 KL Divergence와 실제 분포의 엔트로피 합으로도 표현될 수 있다.

$Cross Entropy Loss = KL divergence + Entropy(P)$

그럼 이와 같이 해석할 수 있다.

“KL Divergence 자체는 실제 분포 P의 엔트로피를 직접적으로 계산하지 않고, $Q$가 $P$를 얼마나 잘 대체할 수 있는지만을 평가한다”

실제 분포 $P$의 엔트로피를 직접적으로 계산한다는 것은 해당 분포의 내재된 불확실성까지 고려한다는 것을 의미한다.

이를 Knowledge Distillation에 적용해보자

“Knowledge Distillation의 첫 번째 항인 KL Divergence는 Teacher Model이 가지는 Softmax 분포의 엔트로피(평균 정보량)을 직접적으로 계산하지 않는다. 즉, Teacher Model의 내재된 불확실성까지 고려하는 것이 아닌, 그저 Student Model과의 분포 간 차이를 고려할 뿐이다. 반면, 두 번째 항인 Cross Entropy Loss는 기존의 ‘실제 분포와 예측 분포 간 차이’를 ‘실제 분포의 내재된 불확실성’까지 고려하는 것이다."

하지만 재미있는 부분은 Teacher과 Student를 비교하는 항에서 KL Divergence 대신 Cross Entropy Loss를 사용해도 동일하게 Knowledge Distillation이 작동된다는 것이다. 모델 학습 자체가 Student의 매개변수에 대해서만 편미분되기 때문이다. Teacher Model의 분포는 고정되어 있기에 $H(T,S) = H(T) + D_{KL}(T||S)$이며, 해당 손실함수 항에서 Student의 매개변수에 대해 편미분하면 $H(T)$는 상수처리가 되면서 소거된다.

즉, Knowledge Distillation 내 실제로 지식이 증류되는 항에서는 KL Divergence를 사용하던 Cross Entropy Loss를 사용하던 결과는 같다.