게임 수학 - 벡터와 행렬

04_01_Introduction: Vectors and Matrices

• 벡터와 행렬은 게임 프로그래밍에 있어서 가장 중요한 역할을 한다
• 이번 강의에서는 벡터의 합과 스칼라 곱과 같은 기본적인 연산과 내적과 벡터곱과 같은 심화 연산을 배운다
• 또한 이번 강의에서는 인접 행렬로 그래프 데이터를 저장하는 것과 행렬의 기본적인 연산을 배운다

04_02_Reading and Writing Vectors

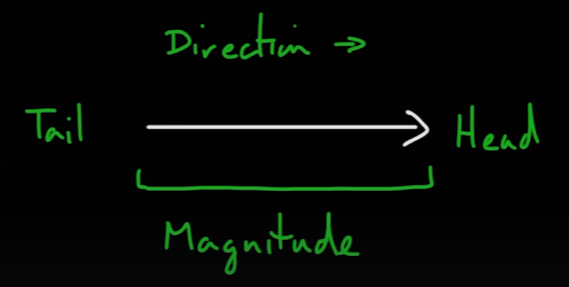
• 벡터는 다음과 같은 구조로 되어 있다.

  • 벡터는 방향(Direction)과 크기(Magnitude)를 가지고 있는 양을 의미한다
  • 크기가 1인 벡터를 단위 벡터(Unit Vector)라 한다
    

• 벡터를 표시하는 방식은 다음과 같은 방법들이 있다
  

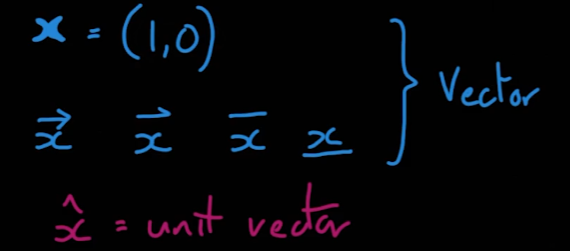
• 벡터의 합과 차는 다음과 같이 나타낼 수 있다
  

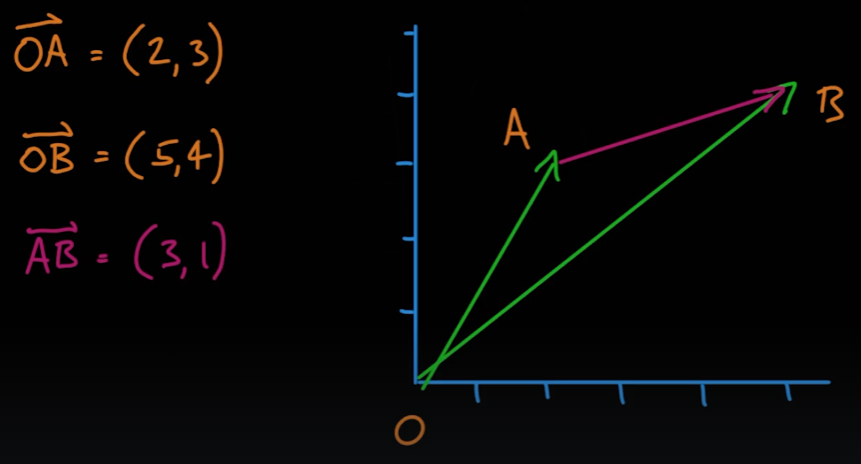
04_03_Magnitude vs Squared Magnitude

• 이차원 벡터의 크기는 다음과 같이 구할 수 있다
  
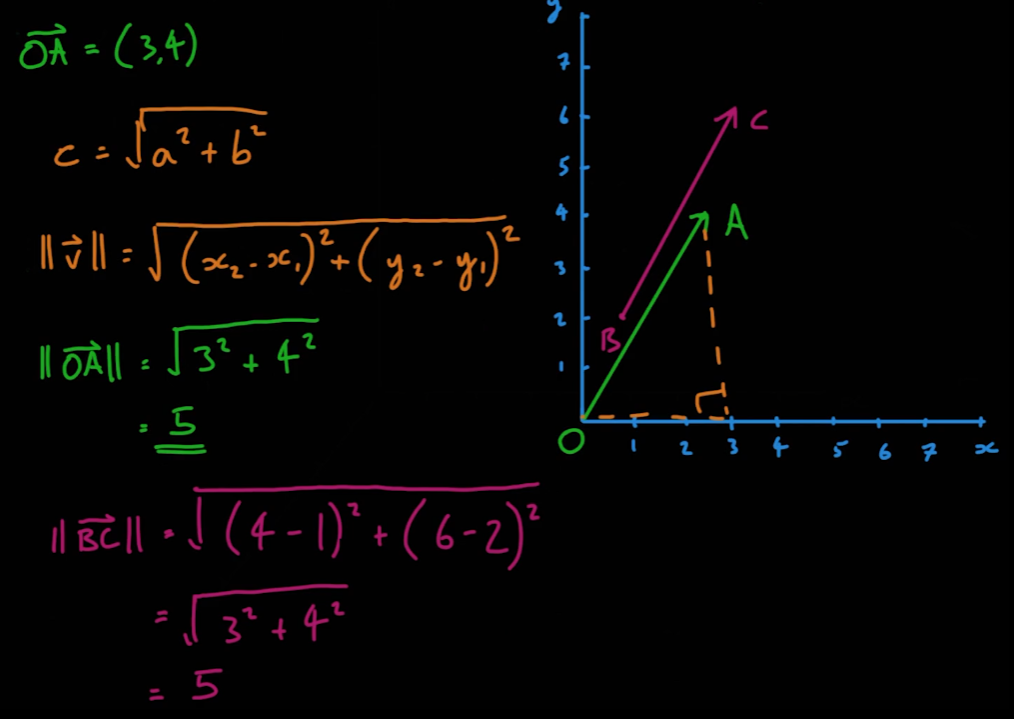
• 삼차원 벡터의 크기는 다음과 같이 구할 수 있다.
  
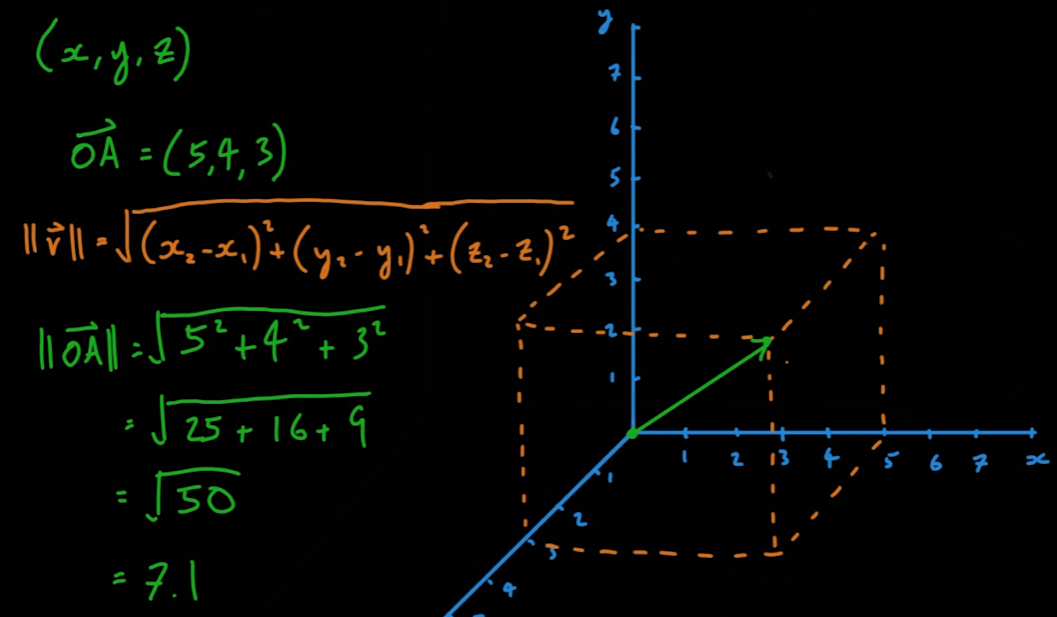
• 거리의 측정 및 비교 등에서는 크기의 제곱을 주로 사용하게 된다.
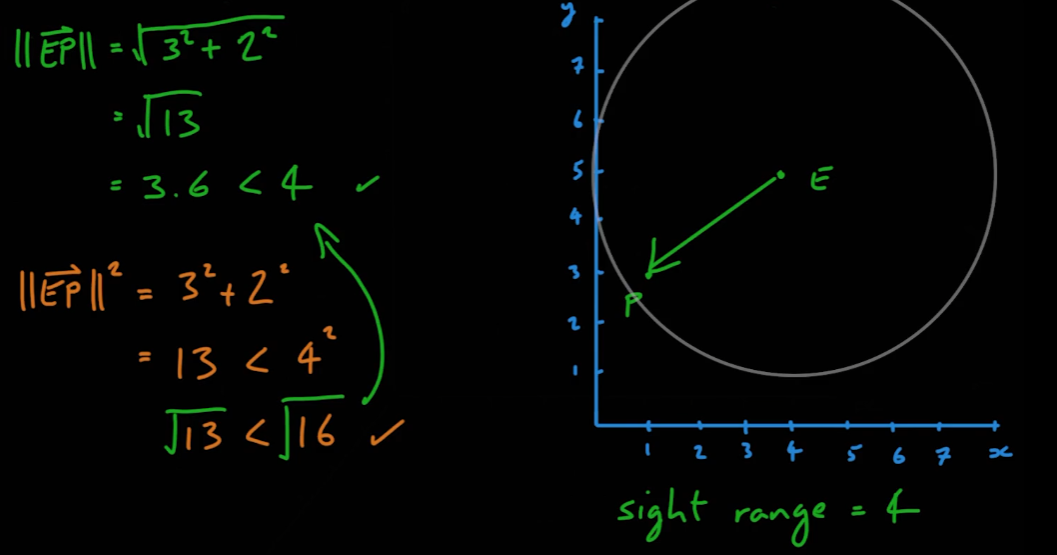
  • 컴퓨터의 제곱근 계산은 매우 무거운 연산이므로 크기의 제곱은 상세한 값을 알 필요가 없을 때 빠르고 유용하게 사용할 수 있다
    

04_04_Coordinate Systems

• 게임 엔진들은 주로 왼손 좌표계를 사용하지만, 3D모델링 툴들은 주로 오른손 좌표계를 사용한다
  
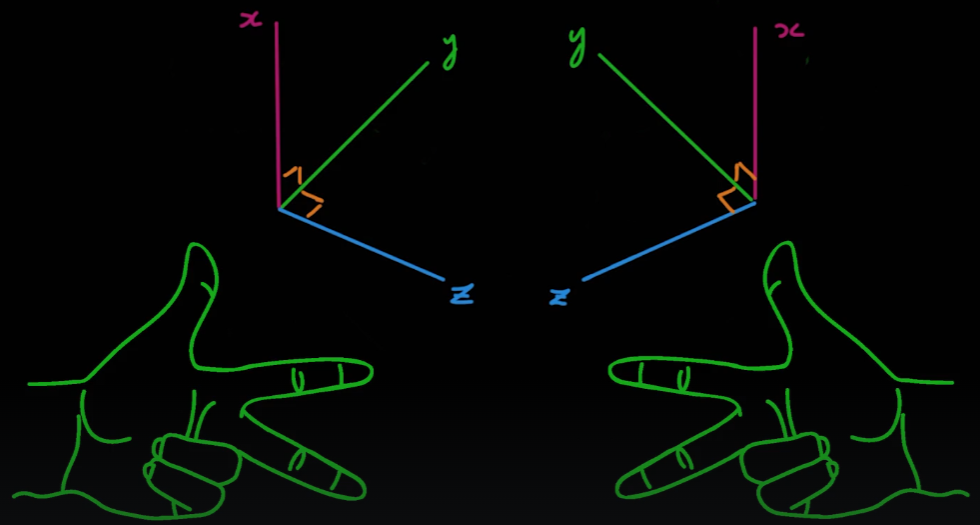
• 이와 같은 상황은 게임 엔진에 3D 모델들을 임포트하여 회전시킬 때 충돌 문제를 야기한다
• 부모 오브젝트 안에 3D모델들을 집어넣고 부모 오브젝트를 회전시키면서 회전축 충돌을 극복할 수 있다

04_05_Vector Addition

• 벡터의 합은 다음과 같이 구한다
  
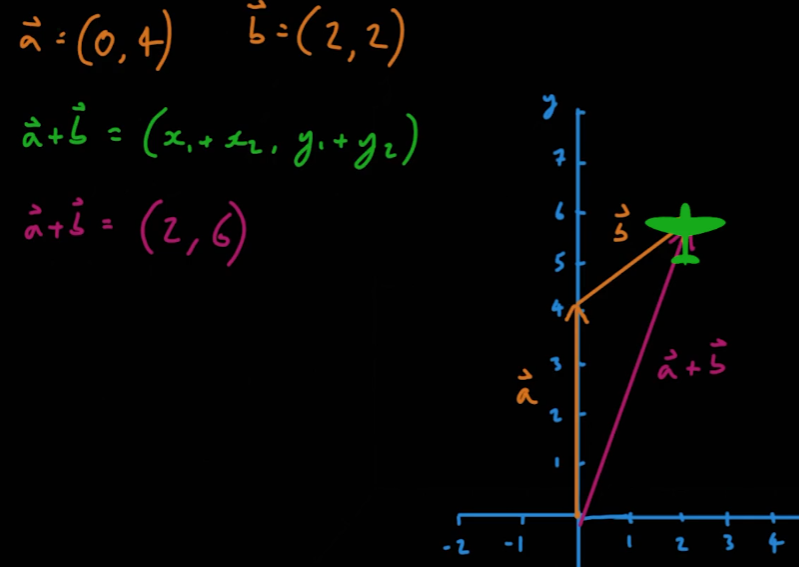
  • 벡터의 합은 순서가 상관이 없다(a + b = b + a)
• 벡터의 차는 다음과 같이 구한다
  
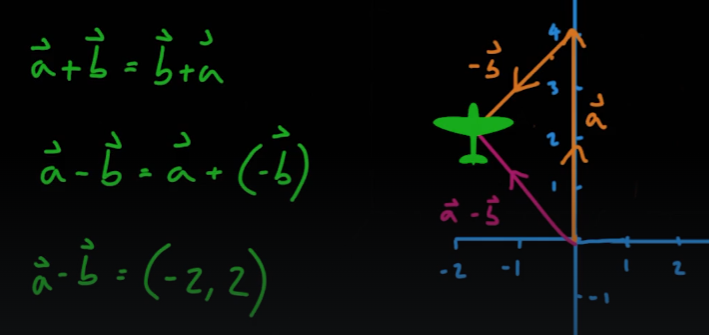
  • 벡터의 차 또한 순서와 관계 없다(a - b = -b + a)
• 카메라 포지셔닝처럼 어떠한 물체에 일정 거리를 둘 때에 벡터의 합과 차를 사용한다

04_06_Scalar Multiplication

• 스칼라 곱으로 벡터의 크기를 변경시킬 수 있다
  • 게임 내에서 속도의 크기를 변화시킬 때 주로 사용
• 다음과 같은 식에서 -1을 스칼라라고 한다.
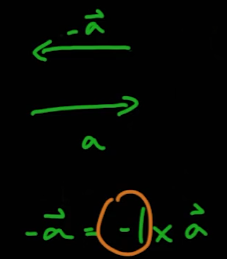
  • 스칼라는 크기만 있고 방향을 가지지 않는 양을 뜻힌다
    
• 벡터에 스칼라를 곱하여 방향을 유지하고 크기만을 변경시키는 것을 스칼라 곱이라고 한다

04_07_Normalizing Vectors

• 벡터를 단위 벡터화하는 것을 벡터의 정규화라고 한다
  • 플레이어의 이동 벡터를 플레이어의 방향 등으로 변환할 때 유용하게 사용한다
• 벡터를 정규화하는 방법은 벡터의 각 요소를 벡터의 크기로 나누는 것이다
  

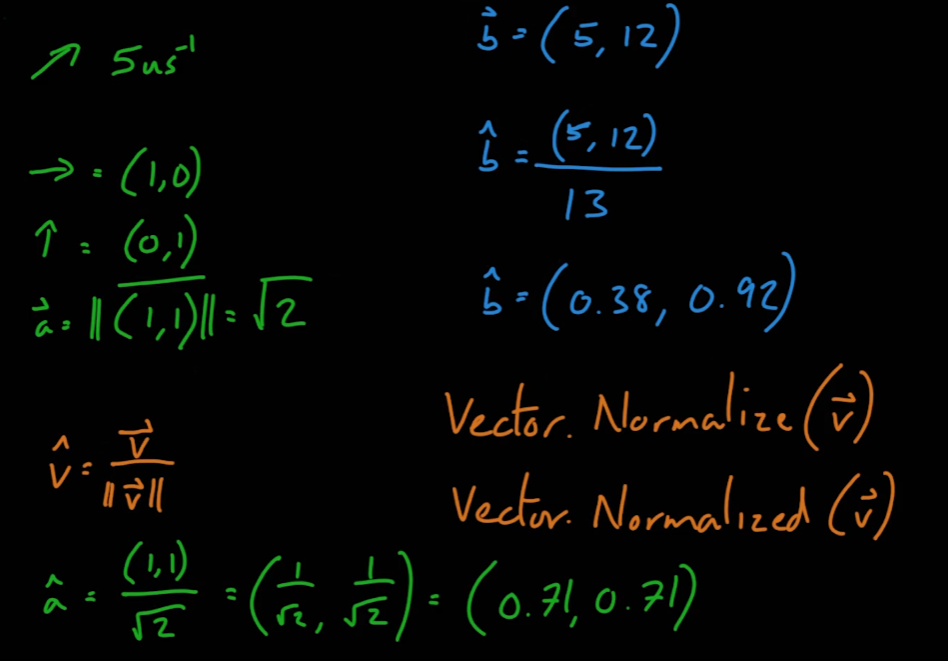
04_08_Zero Vectors

• 벡터의 크기가 0이면 벡터의 방향 또한 (0, 0)이 되어무의미해진다. 이를 제로벡터라 한다

04_09_Dot Product

참고 자료

• 벡터의 내적은 다음과 같이 구할 수 있다
  
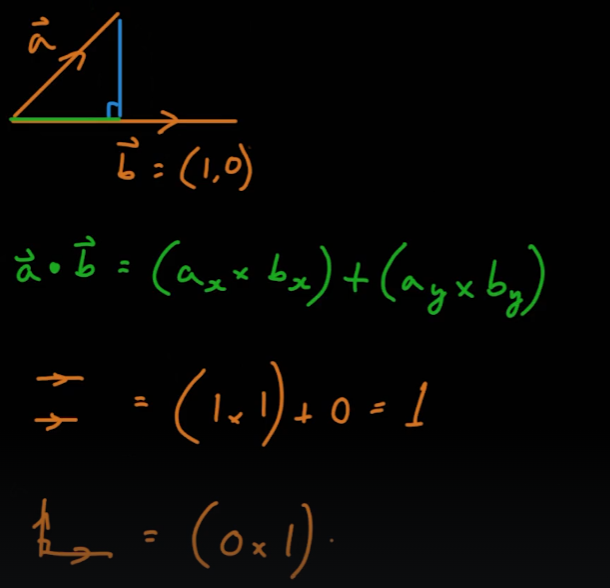
• 벡터의 내적은 두 벡터의 사이각에 따라 크기가 달라진다.
  • 사이각이 예각이면 내적은 양의 힘으로 작용
  • 사이각이 직각이면 내적은 0이다
  • 사이각이 둔각이면 내적은 음의 힘으로 작용
• 벡터 a와 단위 벡터 b의 내적은 다음의 식으로 구할 수 있다.
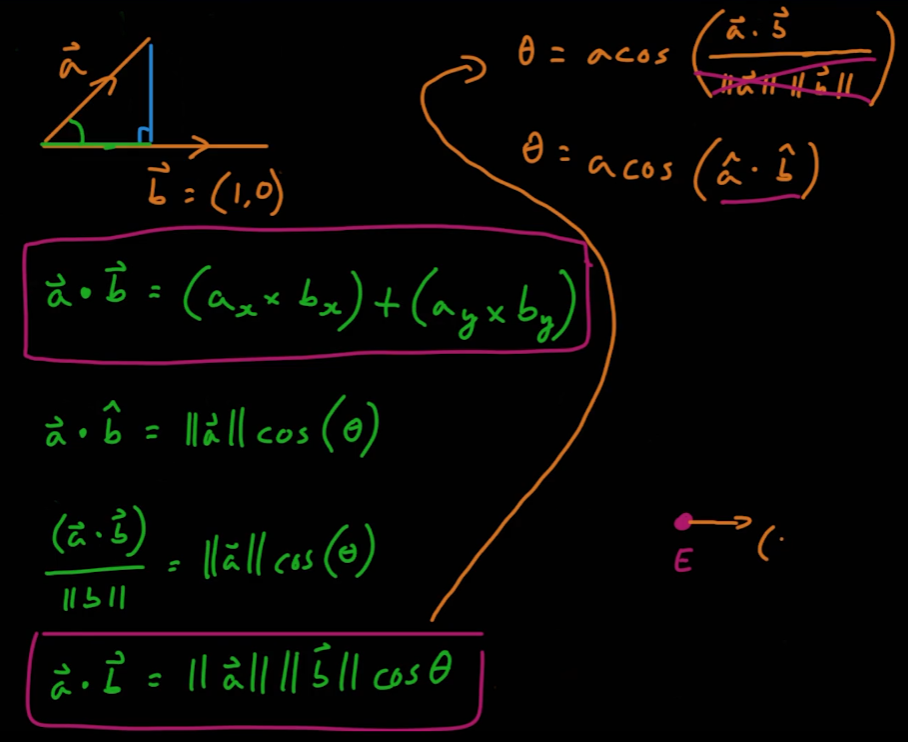
  • 이는 두 벡터 사이각의 크기를 유도할 수 있다
    

04_10_Cross Product

참고 자료

• 벡터의 외적은 3D좌표계에서만 계산 가능하다
• 두 벡터 A, B 의 외적 A X B 는 두 벡터에 동시에 수직이고, 그 크기는 |A|*|B|*sinθ 가 된다.
  

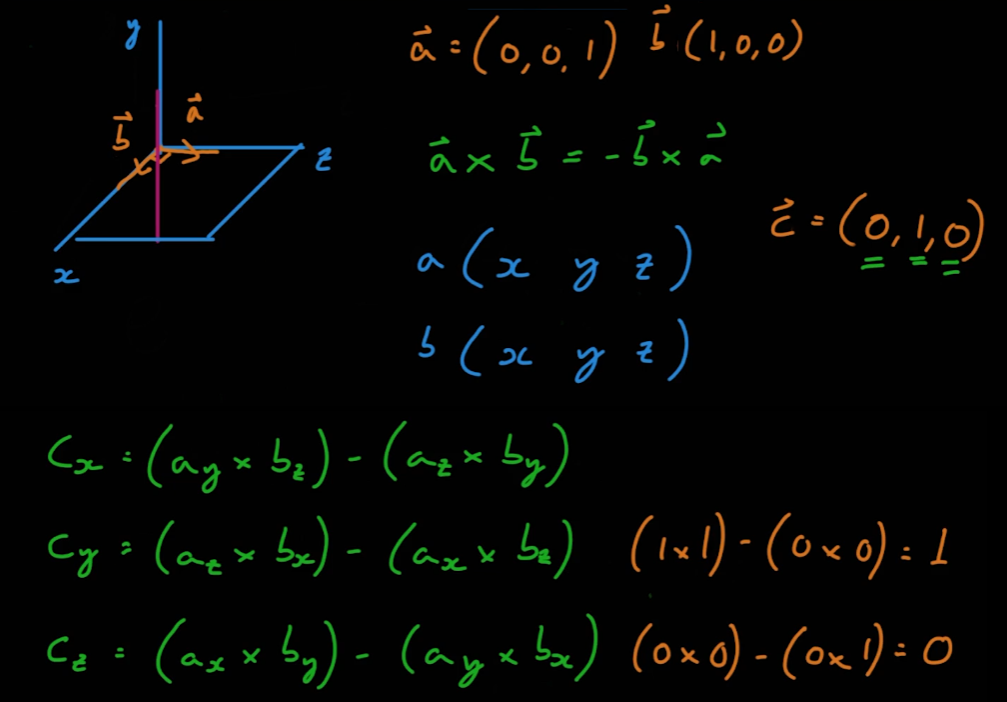
04_11_Reflection

참고 자료

• 반사 벡터를 구하는 방법은 다음과 같다
  

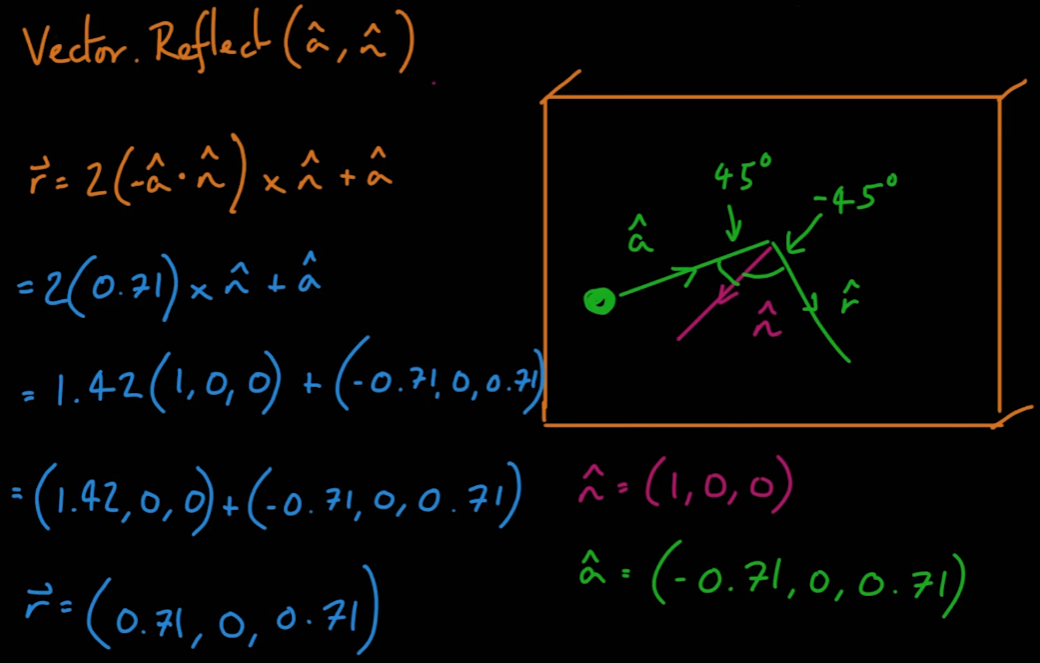
04_12_Project on a Plane

참고 자료

• 벡터의 투영을 구하는 방법은 다음과 같다
  

04_13_What is a Matrix

• 행렬(Matrix)은 수 또는 변수 등의 일련의 개체들을 행(Row)과 열(Column)에 맞추어 직사각형 모양으로 순서 있게 배 열하여 괄호[ ]로 묶은 것
• 열의 크기가 1인 행렬을 행 벡터(Row Vector)라 하고, 행의 크기가 1인 행렬을 열 벡터(Column Vector)라 한다.
• 어떤 행렬의 행과 열을 서로 맞바꾼 행렬을 전치행렬이라 한다.
  
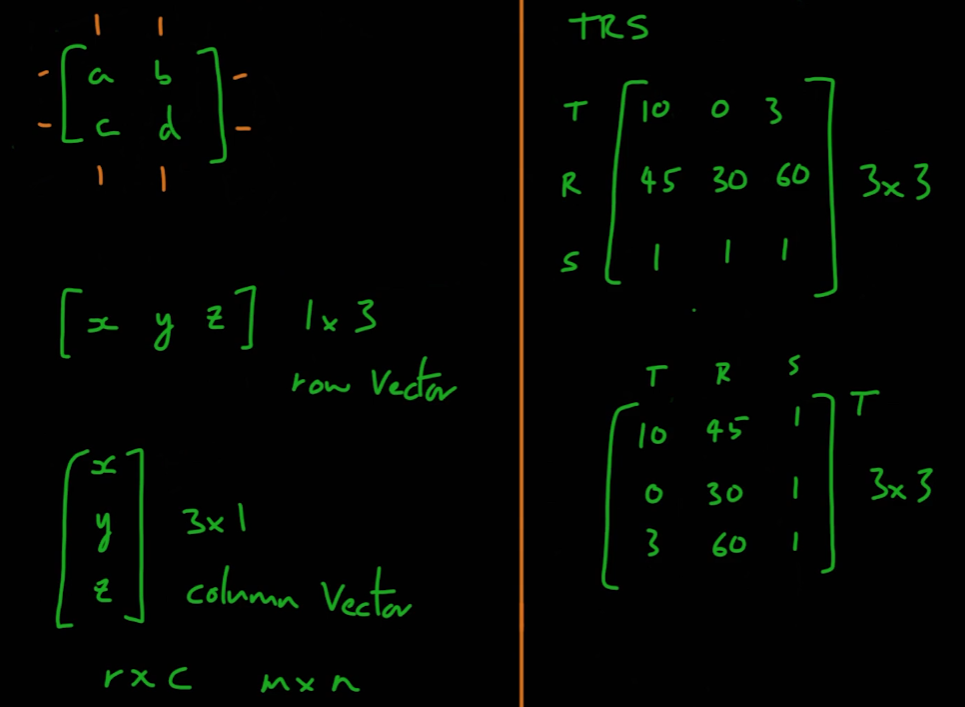
  • 위의 예시에서 행렬 xyz행렬과 TRS 행렬들은 서로 전치인 행렬들이다
• 행렬 a가 있을 때 그 행렬의 원소들을 a11, a12, ...등으로 표현한다

04_14_Addition and Scalar Multiplication

• 행렬의 합은 각 위치에 있는 요소의 합이다
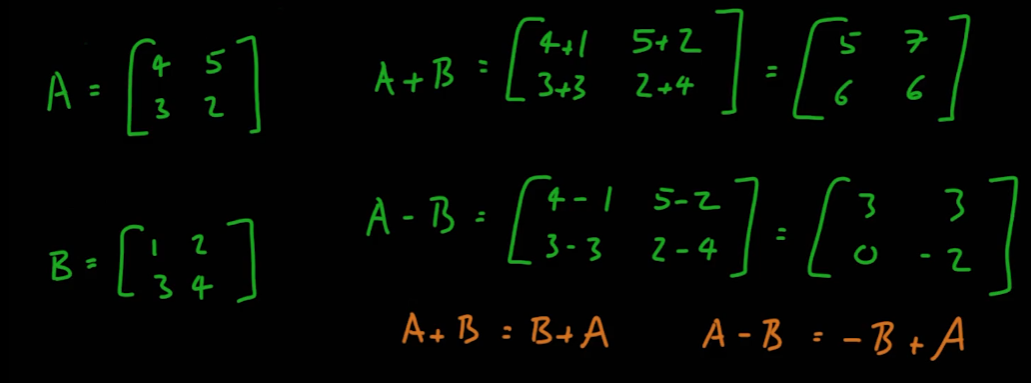
  • 행렬의 합은 서로 다른 모양의 행렬에는 적용할 수 없다
    
• 의 스칼라 곱은 각 위치에 있는 요소를 스칼라만큼 곱한 값이다
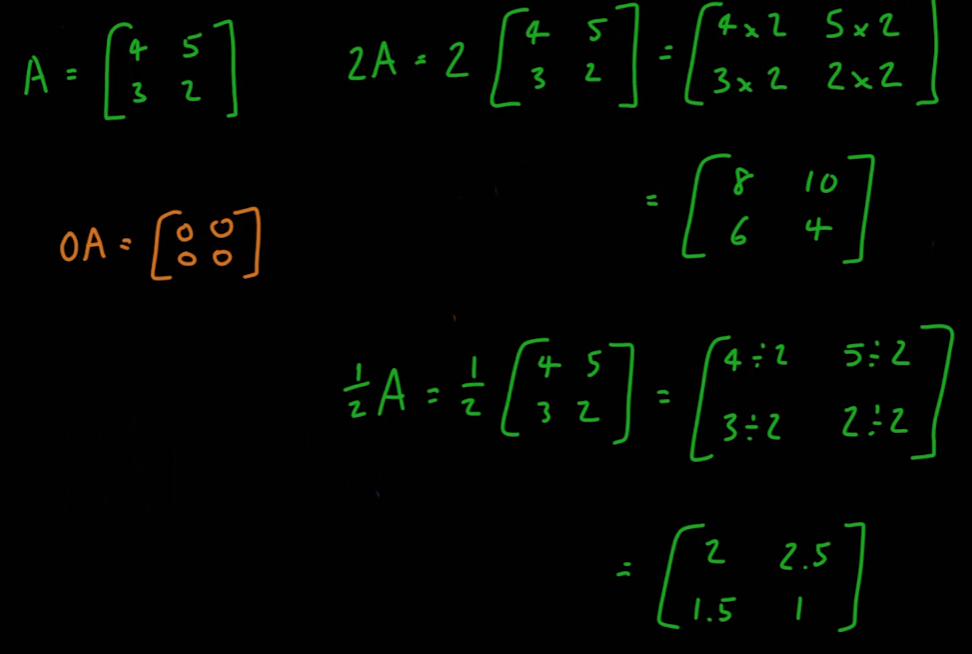
  • 행렬에 0을 곱하게 되면 모든 요소가 0인 행렬이 된다
    

04_15_Adjacency Matrix

• 인접 행렬을 앎으로써 행렬곱과 경로찾기를 좀 더 쉽게 할 수 있다
• 방향이 없는 그래프의 연결상태를 다음과 같은 인접행렬로 표현할 수 있다.
  
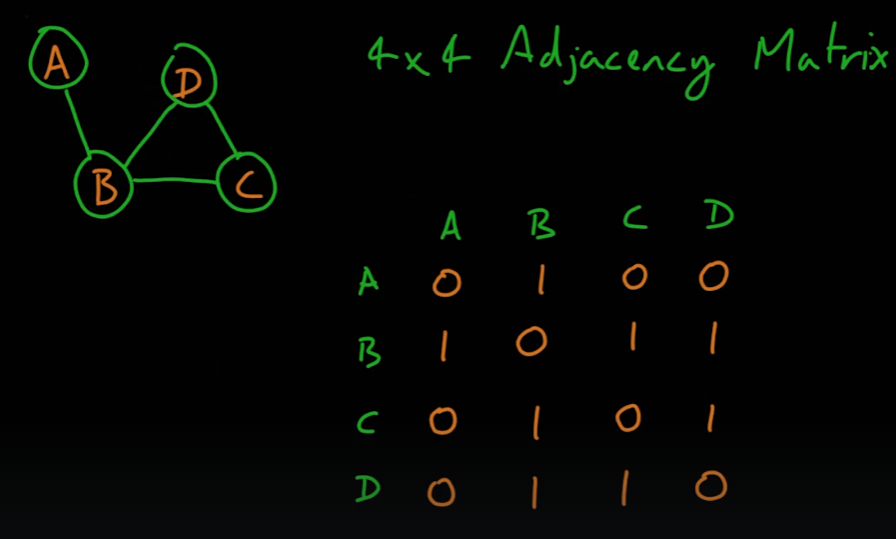
• 방향이 있는 그래프의 경우에는 다음과 같이 표현할 수 있다
  
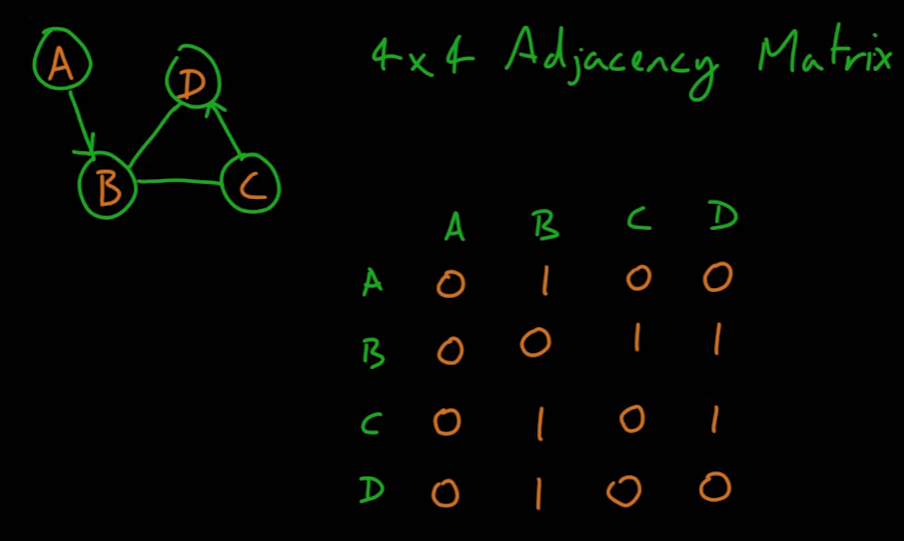
• 가중치가 있는 그래프의 경우 다음과 같이 표현할 수 있다
  

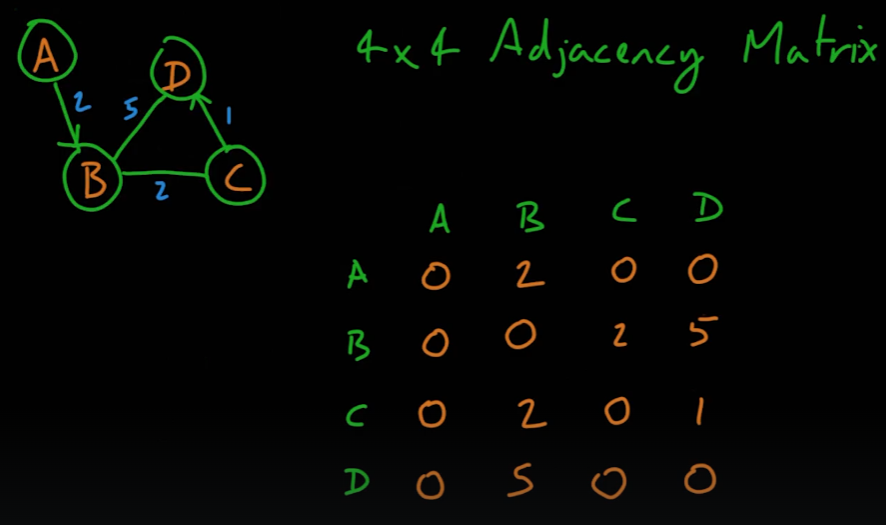
04_16_Matrix Multiplication

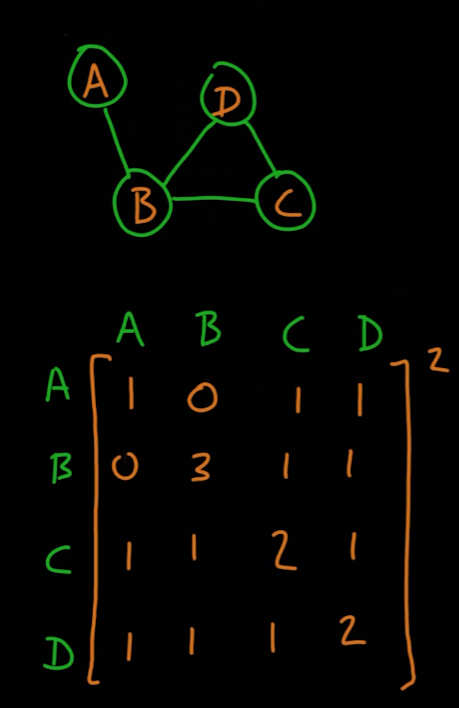
• 04_15의 첫 번째 예시의 행렬을 제곱하면 다음과 같은 결과가 나오게 된다
  • 이는 노드끼리 연결된 선을 두 번 거쳐 자기 자신에게 돌아오는 방법, 즉 다른 노드와 연결된 선의 개수를 의미한다
  • 즉 인접행렬의 n제곱은 노드끼리 연결된 선을 n번 거쳐 자기 자신에게 돌아오는 방법의 개수를 의미한다
    
• 행렬곱은 행렬의 모든 내적곱에 대한 행렬이다. 예시는 다음과 같다.
  

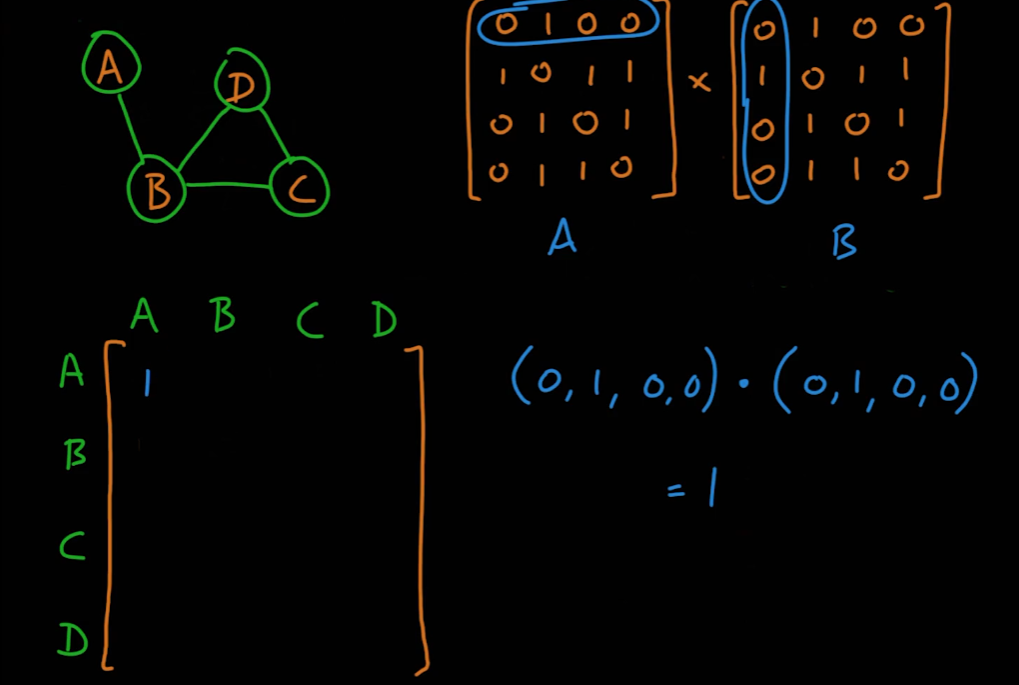
04_17_Identity Matrix

• 단위행렬은 어떤 행렬 A와 곱했을 때 결과가 A가 나오는 행렬이다.
  
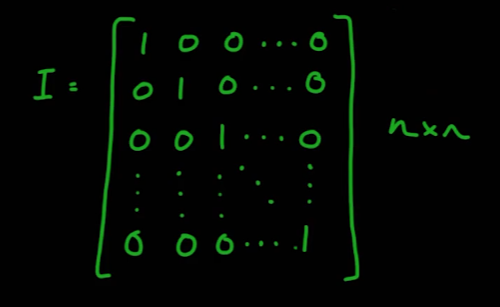
• 행렬곱은 순서변경이 되지 않지만 단위행렬에 대한 행렬곱은 순서를 변경할 수 있다

04_18_Determination

참고 자료

• 3X3행렬의 행렬식을 구하는 법은 다음과 같다
  
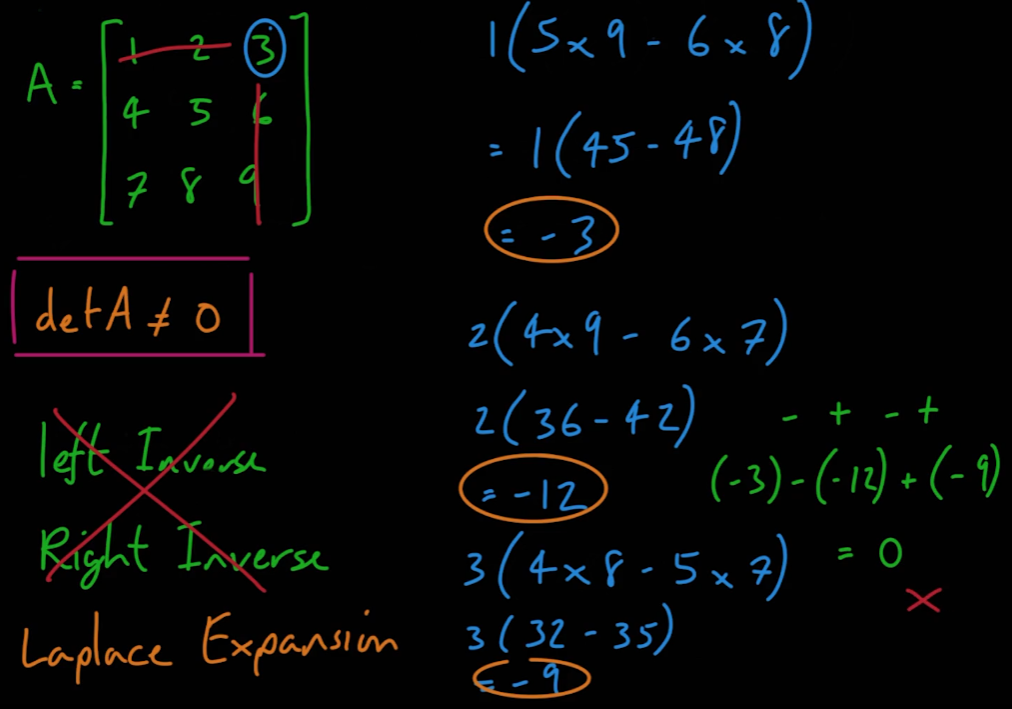
• 행렬식의 값이 0인 행렬들은 역행렬이 존재하지 않는다.

04_19_Matrix Inverse

• 행렬은 나눗셈이 매우 복잡하므로 역행렬을 구하여 대신 처리한다
  • 역행렬이란 어떤 행렬 A와 곱했을 때 곱셈에 대한 항등원인 단위행렬이 나오게 하는 행렬이다
• 2X2행렬의 역행렬은 다음과 같은 과정을 거쳐 얻는다
  
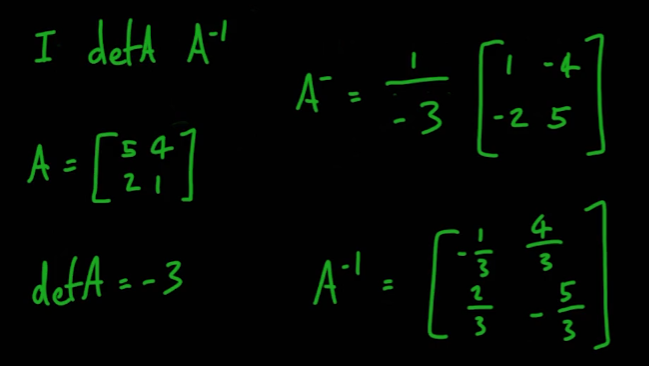
• 3X3행렬의 역행렬은 다음과 같은 과정을 거쳐 얻는다