게임 수학 - 각도와 원

03_01_The Circle

• 자신을 중심으로 원 모양의 구역에 미사일을 쏠 수 있는 터렛이 있다.
• 이 때 터렛이 미사일을 쏠 수 있는 구역의 외곽을 원둘레(Circumference)라 하고, 터렛의 위치를 원의 중심(Origin)이라 한다.
• 터렛에서 외곽까지 그은 직선을 반지름(Radius)이라 하고, 외곽의 한 점에서 터렛을 지나 반대쪽 외곽까지 그은 점을 지름(Diameter)이라 한다. 지름은 반지름 * 2이다.
• 터렛이 특정한 각도 내에만 미사일을 쏠 수 있을 때 터렛의 발사 범위를 부채꼴(Sector)이라 한다.
• 원둘레와 부채꼴이 만나는 지점의 곡선을 호(Ark)라 한다.

03_02 What is Pi?

• 원주율(pi)는 원의 둘레를 원의 지름으로 나눈 값으로 그리스 문자 p로 표현한다.
• 원주율의 값은 모든 원에 대해 항상 고정되므로 원주율과 특정 값을 이용해 다른 값을 구할 수 있다.
• 반지름이 1인 원에 대한 예시
  • 반지름이 1인 원은 단위원(Unit Circle)로써 원과 삼각함수 등에서 자주 사용되는 도형이다.
  • 해당 원의 지름은 반지름 * 2인 2이고, 해당 원의 둘레는 지름 * pi인 2pi이다.

03_03_Degrees and Radians

• 한 바퀴는 360도이다. 원을 360개의 파이 조각으로 쪼개면 하나의 조각은 1도만큼의 각을 갖게 된다.
  • 한 바퀴를 360도로 정의한 정확한 연혁은 밝혀지지 않았으나 고대 바빌로니안의 특유의 60진법에서 파생되었다는 설이 유력하다.
• 라디안은 단위원의 반지름과 호의 길이가 정확히 일치할 때의 각도를 뜻한다. 따라서 하나의 원은 2pi 라디안만큼의 각도를 가진다.
  • 즉 360도는 2pi라디안, 180도는 pi라디안이다.

03_04_Triangles

• 삼각형의 세 각의 합은 항상 180도이다.
• 모든 변의 길이가 같은 정삼각형의 모든 내각은 60도이다.
• 두 변의 길이가 같은 삼각형은 이등변삼각형이다. 이등변삼각형은 빗변과 접하는 두 개의 각이 서로 일치하다.
• 예각삼각형은 모든 각의 크기가 90도를 넘지 않는 삼각형이다.
• 직각삼각형은 한 각의 크기가 90도인 삼각형이다.
• 둔각삼각형은 한 각의 크기가 90도를 넘는 삼각형이다.

03_05_Pythagorean Theorem.txt

• 피타고라스의 정리 : 직각삼각형의 밑이 a, 높이가 b, 빗변이 c일 때, a^2 + b^2 = c^2이다.
• 피타고라스의 정리 증명
  • 한 변의 길이가 a+b인 정사각형의 가운데에 한 변의 길이가 c인 정사각형을 넣으면 c^2 = (a + b)^2 - 4(1/2ab)가 된다.
  • 위의 식을 풀면 c^2 = a^2 + b^2가 된다.

03_06_Sine, Cosine, and Tangent

• 해당 강의에서는 삼각함수에서 가장 기초적인 세 가지 함수의 관계를 알아본다.
• 좌표공간 (0, 0)에 반지름이 1인 원이 위치한다. 그리고 해당 원의 둘레에 한 점이 있다고 치자.
• 해당 점과 x축과의 직선거리가 바로 sine, 해당 점과 y축과의 직선거리가 cosine, 그리고 sine / cosine이 바로 tangent이다.
• sin(0) = 0, cos(0) = 1, tan(0) = 1이다. 반대로 sin(90) = 1, cos(90) = 0, tan(90) = X이다.
• sin은 높이 / 빗변, cos은 밑변 / 빗변, tan은 높이 / 밑변이다. 해외에서는 이를 쉽게 외우기 위해 SOH CAH TOA라 묶어 부른다.

03_07_The Sine Rule

• 사인 법칙을 이용해 세 각과 한 변이 주어진 삼각형의 나머지 두 변의 길이를 구할 수 있다.
• 삼각형의 내각 A, B, C가 주어지고 그 각과 마주보는 변을 각각 a, b, c라고 할 때 사인 법칙은 다음과 같다.
  • a / sin(A) = b / sin(B) = c / sin(C)
• A = 32도, B = 68도, b가 10일 때 A의 값은 10 * (sin(32) / sin(68)) = 5.72...가 된다.

03_08_The Cosine Rule

• 코사인 법칙을 이용해 한 각과 두 변의 길이가 주어진 삼각형의 나머지 변의 길이를 구할 수 있다.
• 삼각형의 내각 A, B, C가 주어지고 그 각과 마주보는 변을 각각 a, b, c라고 할 때 사인 법칙은 다음과 같다.
  • c^2 = a^2 + b^2 - 2ab * cos(C)

03_09_The Sine & Cosine Rules Explained

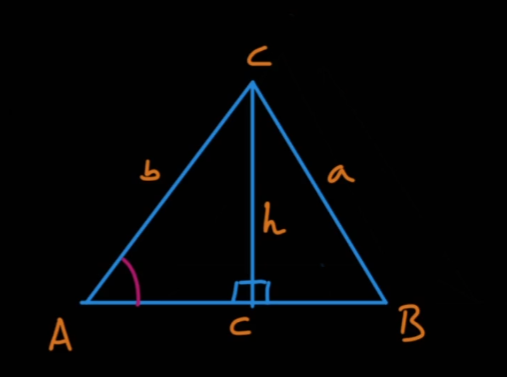
• 위와 같은 그림에서 sin법칙 유도
  • sin(A) = h / b, h = b * sin(A)
  • sin(B) = h / a, h = a * sin(B)
  • a / sin(A) = b / sin(B) = c / sin(C)

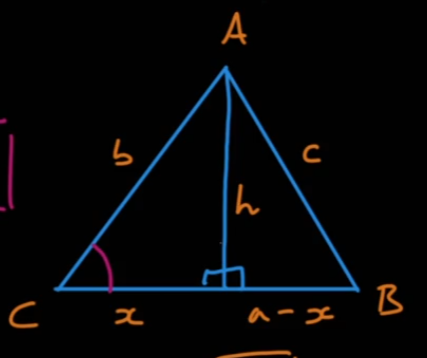
• 위와 같은 그림에서 cos법칙 유도
  • b^2 = x^2 + h^2, c^2 = (a - x)^2 + h^2
  • c^2 = a^2 - 2ax + x^2 + h^2
  • c^2 = a^2 + b^2 - 2ax
  • cos(C) = x / b, x = b * cos(C)
  • c^2 = a^2 + b^2 - 2ab * cos(C)

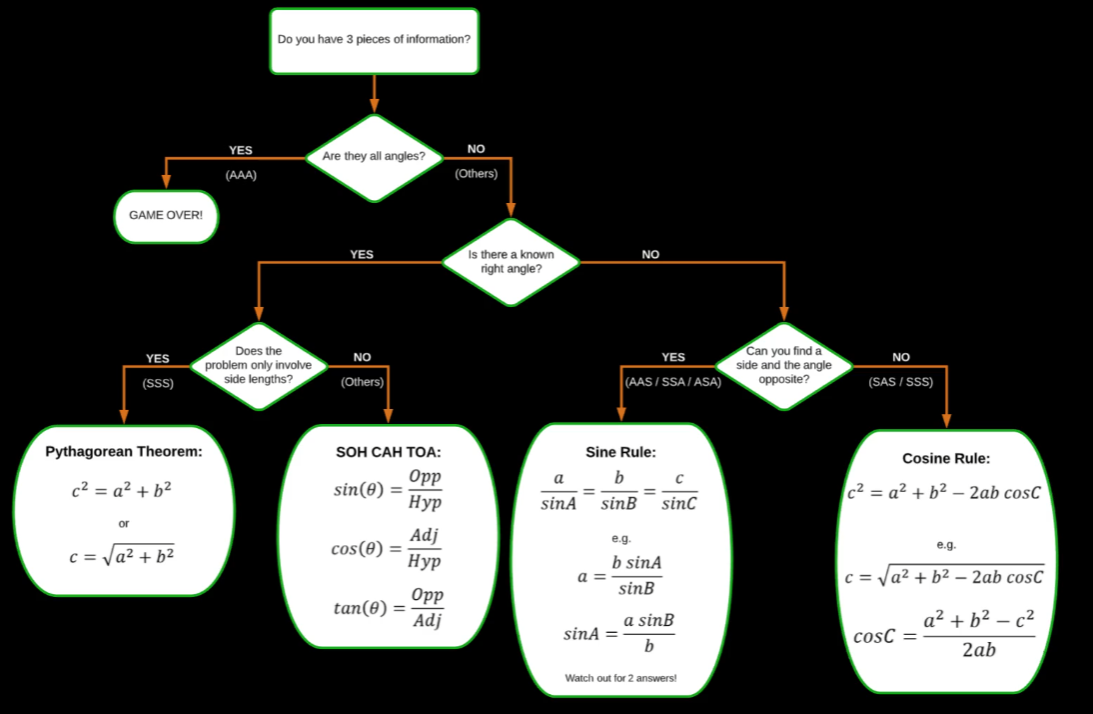
03_10_Solving Any Triangle

03_11_Graphing Sine, Cosine, and Tangent

• 사인 함수 그래프
  

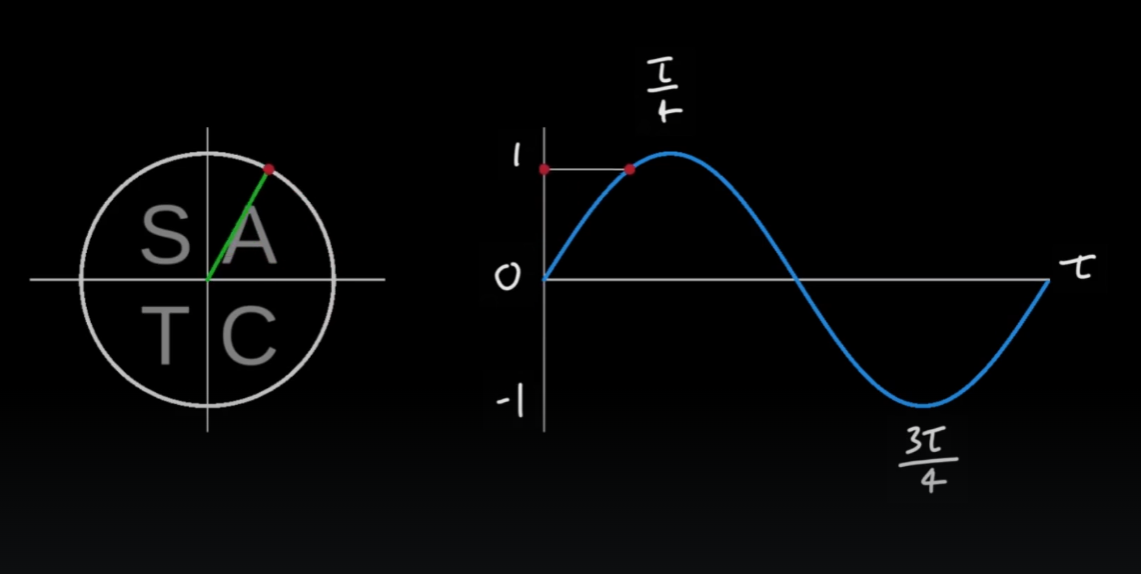
• 코사인 함수 그래프
  

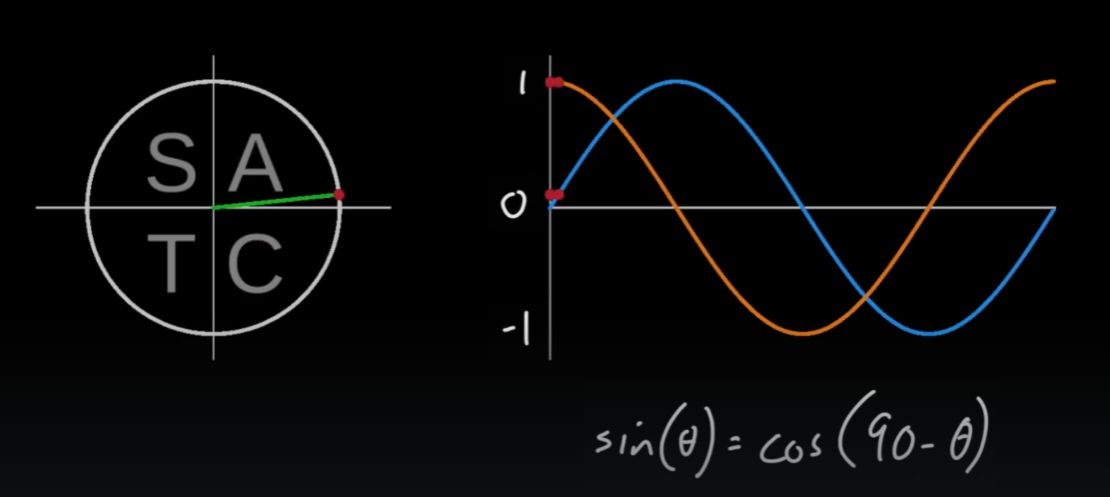
• 탄젠트 함수 그래프
  

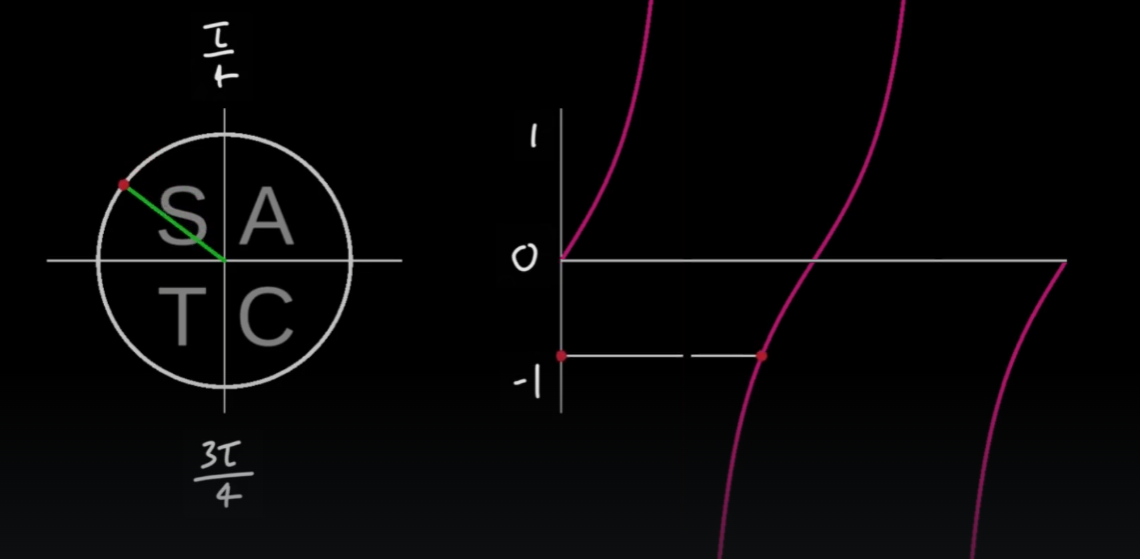
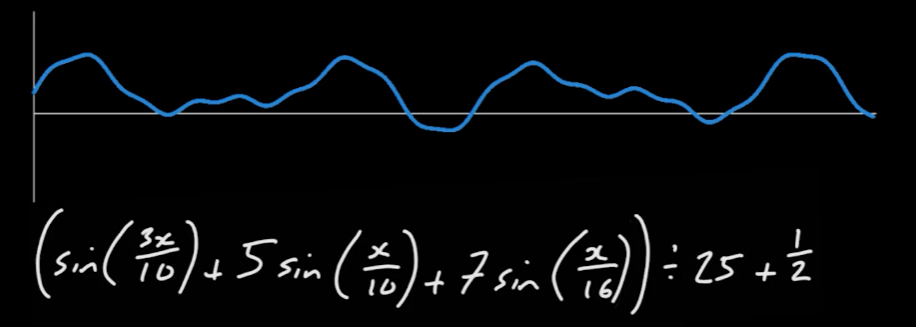
03_12_Manipulating Sine Waves

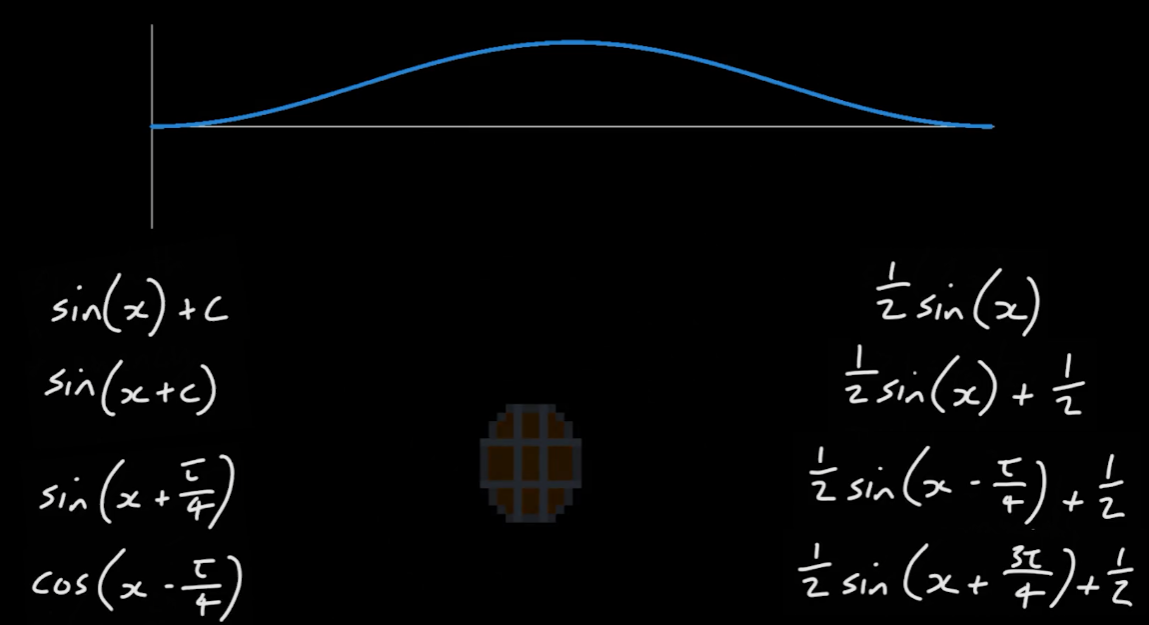
• 사인 그래프는 물체의 부드러운 변화를 구현하는 데에 유용하다
  • 터렛의 기본 움직임을 구현할 때 좌우를 살피는 것처럼
  • 불빛이 밝아졌다 어두워질 때를 구현하는 것
• 사인 그래프를 90도 앞으로 밀면 코사인 그래프가 된다
  

03_13_Combining Waves

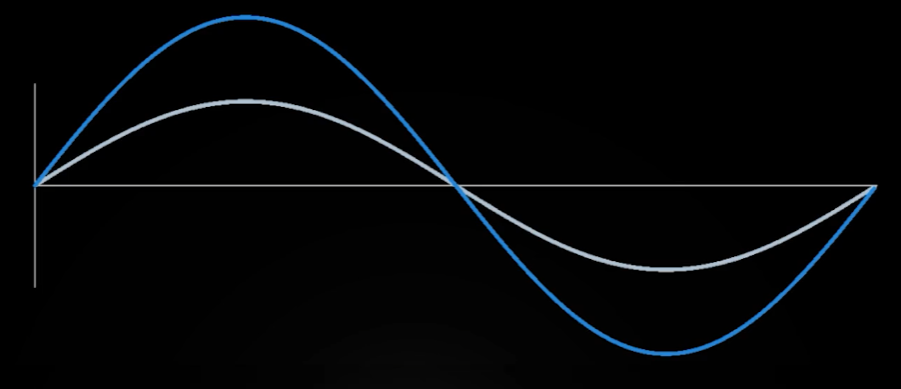
• 증폭 간섭

  • sin(x) + sin(x) = 2sin(x)
    

• 상쇄 간섭

  • sin(x) + sin(x + pi / 4) = sin(x) - sin(x) = 0
    

• 변형 간섭

  • sin(x) + sin(2x)
  • 이러한 변형은 자연스러운 촛불이나 트릭키한 플랫포머 발판 등에 유용하게 사용할 수 있다