통계학 1회차 세션 -(2) 편차,분산,표준편차,뵤본분포

🔥오늘 깨달은 것

🔥오늘 헷갈린 개념

⭐

• 편차 -> 분산 -> 표준편차 개념
• 많은 데이터를 대상으로 효과적인 통계분석을 위해 표본 추출 이뤄지는 중
• 모집단, 표본 개념
• ⭐ 중심극한정리 : 표본의 분포를 가지고 모집단의 분포를 추정하며, 해당 과정에서 무수히 많은 경우의 수의 표본이 생성될 수 있다. 표본 크기가 충분히 크다면 어떤 분포에서도 표본평균이 정규분포를 따른다.
• 정규분포 개념, 평균치에서 확률이 가장 높음
• 표준정규분포: 정규분포에서 평균 0, 분산 1을 가지는 경우 => 데이터분석시 표준화라고 지칭
• ⭐:
  • 데이터분석시 표준화가 필요한 경우: 머신러닝 모델을 만들 때, 데이터의 범위가 많이 차이나는 경우.
  • ex) 최근 일주일 접속일수의 1과 결제금액의 1 은 같은 의미가 아니며, 범위가 큰 데이터의 경우 숫자가 가지는 절대치를 잘못 받아들일 수 있어 표준화는 반드시 필요

1. 평균 : 모든 값의 총 합을 개수로 나눈 값

   df[].mean()

2. 중간값 : 숫자를 작은 순서대로 정렬했을때, 가운데 위차한 값

   df[].median()

3. 최빈값 : 가장 자주 등장하는 값

   df[].mode()

4. 편차 : 각 점수가 평균에서 얼마나 떨어져 있는지를 계산한 값

   편차= 점수-평균

   df['편차'] = df['점수'] - df['점수'].mean()

5. 분산 : 편차의 합이 0으로 나오는것을 방지하기 위해 생성된 개념
   => 편차를 제곱해서 평균낸 값
   

   df[].var() -> 표본의 분산
   df[].var(ddof=0) 모집단의 분산

6. 표준편차 = 분산의 제곱근
   데이터 값들이 평균에서 얼마나 떨어져 있는지를 나타내는 척도
   ⭐원래 데이터 값과 동일한 단위로 변환
   

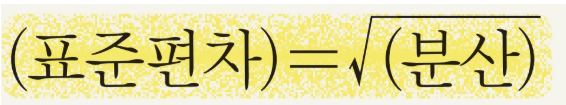
   df[].std() -> 표본의 표준편차
   df[].std(ddor=0) -> 모집단의 표준편차

7. 모집단
   : 조사 하고 싶은 전체 대상

8. 표본
   : 모집단에서 일부만 뽑은 대상
   -> 우리가 실제로 조사할 수 있는 데이터

9. 표본평균
   :표본의 평균값

10. 표본분포
    : 표본의 분포
    -> 표본이 흩어져 있는 정도

11. 표본평균의 분포
    : 여러 표본의 평균을 모아 만든 분포
    -> 데이터가 충분한 경우 정규분포를 따름(= 중심 극한 정리)

• 정규분포 -> ⭐ 확률 예측 가능
  

12. 표준오차
    : 표본의 표준편차 = 표본평균의 평균과 모평균의 차이
    => 표본 多 -> 표준오차 少