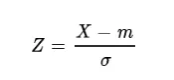🧡오늘 개념 중 가장 중요한것

• 표본의 분포를 가지고 모집단의 분포를 추정하며, 해당 과정에서 무수히 많은 경우의 수의 표본이 생성될 수 있습니다. 표본 크기가 충분히 크다면 어떤 분포에서도 표본평균이 정규분포를 따른다는 것이 중심극한정리 입니다.
• 정규분포는 종 모양을 띄고 있으며, 분포는 좌우 대칭의 형태입니다. 평균치에서 그 확률이 가장높습니다.
• 정규분포에서 평균 0, 분산 1을 가지는 경우, 이를 표준정규분포라고 합니다. 데이터분석시 이를 표준화라고 부릅니다.
• 데이터분석시 표준화가 필요한 경우:
  • 머신러닝 모델을 만들 때, 데이터의 범위가 많이 차이나는 경우.
  • 예시로 최근 일주일 접속일수의 1과 결제금액의 1 은 같은 의미가 아니며, 범위가 큰 데이터의 경우 숫자가 가지는 절대치를 잘못 받아들일 수 있어 표준화는 반드시 필요합니다.**

🔥오늘 깨달은 것

🔥오늘 헷갈린 개념

• 표본의 값이 충분히 大 -> 분포는 종 모양의 정규분포를 따름

⭐모르는 개념

• 모평균: 어떤 모집단의 분포에서의 확률 변수의 평균값.

1. 정규분포
   

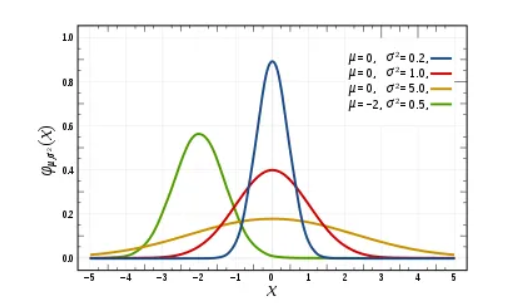
특징:

• 분포는 평균 중심으로 좌우대칭의 형태
• 곡선= 각 확률값 나타냄, 모두 더하면 1
  -> ( 동전 앞면이 나올 확률 1/2+ 뒷면이 나올 확률 1/2 =1 )
• 평균과 분산(퍼진정도)에 따라 다른 형태를 가짐
• 빨간 그래프 = 표준정규분포 : 평균 0,부산 1 가지는 경우

표준화
-> 각각의 그래프는 평균과 분산값에 따라 다르게 그려질 수 있어 이를 통일하기 위해, 정규 분포의 평균과 분산 값을 통일하는 작업을 하게됨

• 공식 : x(확률변수),m(평균), 분모(표준편차)
  

신뢰구간, 신뢰수준

• 모든 데이터는 표본을 추출하는 순간 불확실성을 갖게 됨
• 신뢰도 : 데이터의 불확실성
• 신뢰구간 : 특정 범위 내에 값이 존재할것으로 예측되는 영역
• 신뢰수준 : 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률
  • 신뢰수준 95% : 무작위로 표본을 추출했을떄, 100번 중 95번은 신뢰구간 안에 모집단의 값을 포함
  • 신뢰수준 99% : 무작위로 표본을 추출했을때, 100번 중 99번은 신뢰구간 안에 모집단의 값을 포함
• ❗ 주의
  • 신뢰수준 🔼 -> 신뢰구간 넓어짐 -> but,정확한 예측이 어렵기 때문에 95% 보다 99% 신뢰수준이 --더 좋다 말할 수 없음--.

실습

import scipy.stats as st
import numpy as np

sample1 = [5,10,17,29,14,25,16,13,9,17]
sample2 = [21,22,27,19,23,24,20,26,25,23]

df = len(sample1) - 1
mu = np.mean(sample1)
se = st.sem(sample1)

st.t.interval(0.95, df, mu, se)
st.t.interval(0.99, df, mu, se)

⭐⭐코드 분석

• scipy.stats : 안에 평균,표준편차,신뢰구간 같은 계산 쉽게 해주는 함수들 들어있음
• numpy : 숫자 계산을 빠르고 쉽게 도와주는 도구
• df = len(sample1) - 1 자유도 구하는 식
  : 데이터 개수에서 1을 뺀 값
  : 1을 빼는 이유 -> 평균을 이미 알고 있을때 계산 할 수 있는 진짜 자유로운 값 개수 하나 줄어들기 때문
  : ❗자유도 : 데이터 중에서 자유롭게 바뀔 수 있는 숫자의 개수
• se = st.sem(sample1)
  : sem()=표준오차를 구하는 함수
  : 표준오차=평균이 얼마나 믿을만한지 보여주는 값
• ⭐신뢰구간 계산하는 코드
  st.t.interval(0.99, df, mu, se)
  • (신뢰수준, 자유도, 평균, 표준오차)
  • st.t.interval(...) -> 데이터가 적거나 정규분포를 가정하지 못할 때 사용 (소규모 샘플)
  • st.norm.interval(...) -> 데이터가 많고 정규분포라고 믿을 수 있을 때 사용
  • ❗norm :정규분포