위 주제는 밑바닥부터 시작하는 딥러닝2 6강, CS224d를 바탕으로 작성한 글 입니다.

이전 글에서 RNN과 TimeRNN, RNNLM에 대해서 코드를 구현하는 시간을 가졌다.

이전글에서 말했듯 RNN이 장기 기억을 처리하지 못한다는 단점으로 LSTM, GRU와 같은 '게이트가 추가된 RNN'을 많이 사용하는데, 보통 Github 소스나, 논문에서 나오는 LSTM, GRU를 RNN으로 표기하는 것을 보아 정말 많이 쓰인다는 것을 알 수 있다.

RNN의 문제점

Tom was watching tv in his room, mary came into the room. mary said hi to ????

앞에서도 말했듯 "?"에 들어가는 단어는 "Tom"이다. RNN이 답을 하기 위해서는 "Tom이 방에서 TV를 보고 있음"과 "그 방에 Mary가 들어옴"이라는 정보를 기억해야 한다.

이런 정보를 RNN 계층의 은닉 상태에 인코딩해 보관 해둬야 한다.

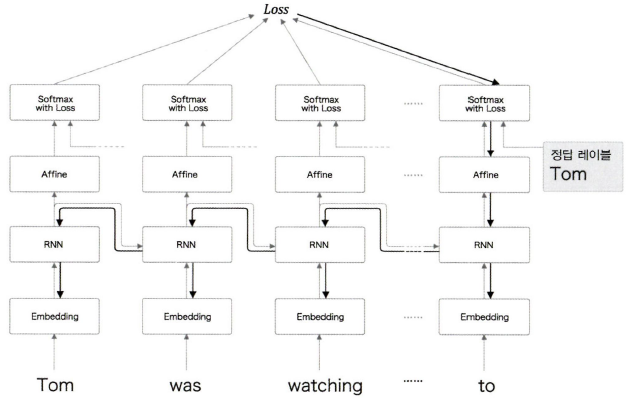
기울기의 흐름을 보여주는 사진인데, RNN 계층이 과거 방향으로 '의미 있는 기울기'를 전달함으로써 시간 방향의 의존 관계를 학습할 수 있다. 문제는 RNN이 기울기를 과거로 전달함으로써 Gradient vanishing이 일어나거나 Gradient exploding이 발생한다는 것이다.

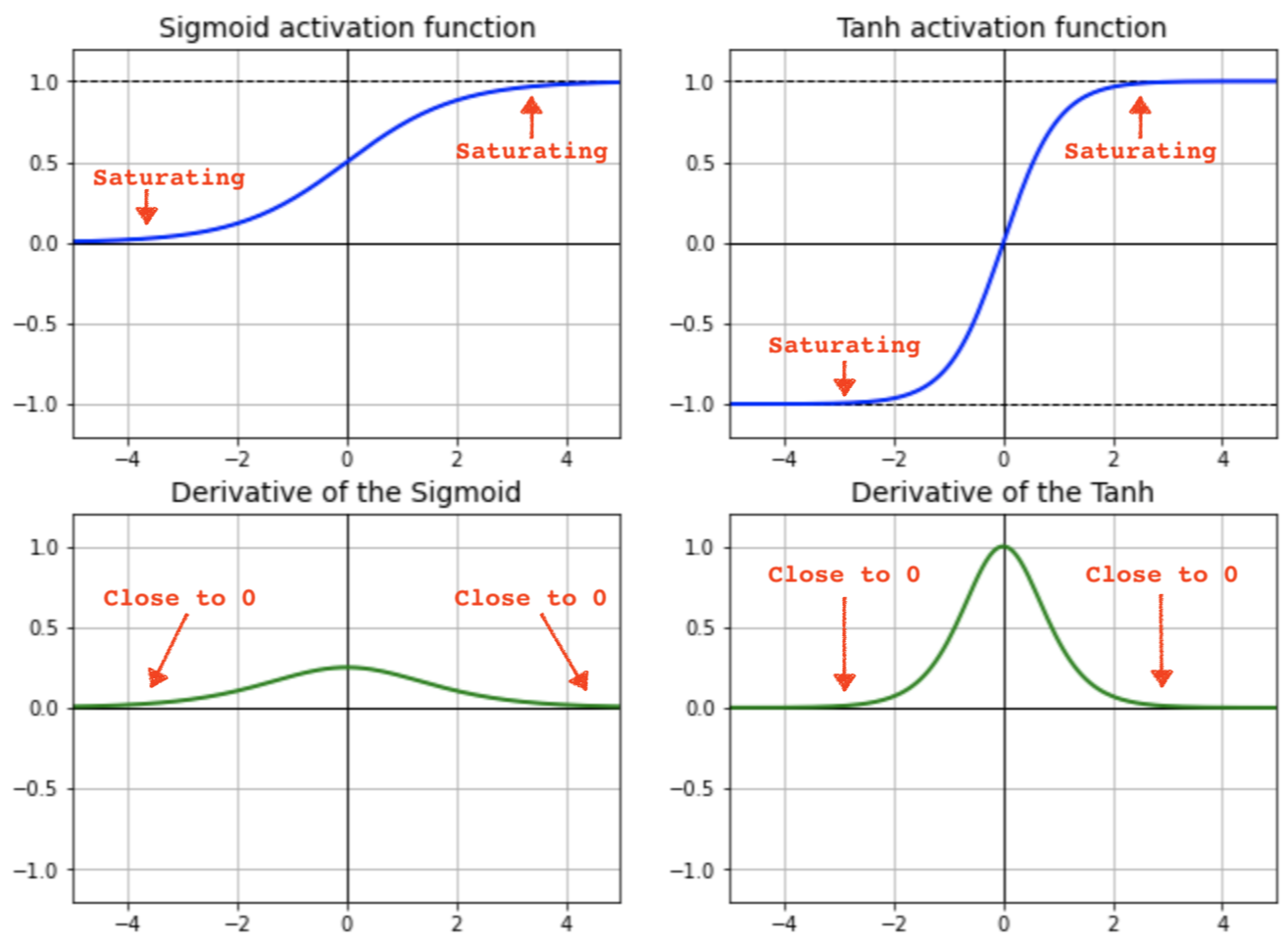
RNN이 기본적으로 Activation function을 "tanh"로 쓰는 이유는 "sigmoid"보다 그나마 gradient에 덜민감하기 때문이다. 하지만 지속적으로 전달되면 vanishing을 피할 수 없다.

기울기 소실( vanishing gradient ), 기울기 폭발( exploding gradient )의 원인

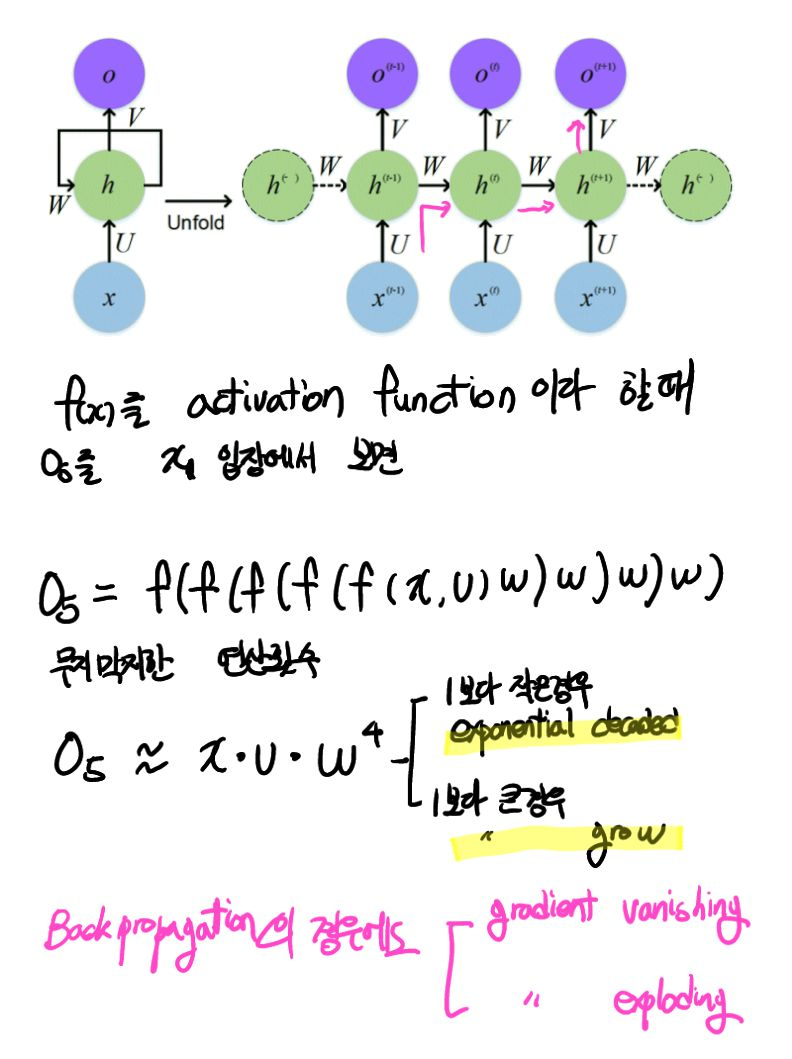
1. tanh의 미분값이 1.0이하이기 때문에 tanh 함수를 T번 통과하면 기울기도 T번 반복해서 작아지게 된다. (Gradient vanishing)

   RNN 계층의 활성화 함수로 ReLU로 바꾸면? 기울기 소실을 줄일 수 있다.
   이유는 Relu는 역전파시 상류의 기울기를 그대로 하류에 흘려보내기 때문이다. 기울기가 작아지지 않는다는 말!! (Improving performance of recurrent neural network with relu nonlinearity 논문을 참고)

2. tanh를 무시하고 'MatMul' 연산에 집중하면
   
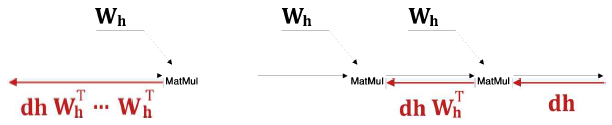
   상류에서 dh라는 기울기가 흘러오고 MatMul에서 dh * Wh.T라는 행렬곱으로 기울기를 계산한다. 이 계산을 반복하는데, 똑같은 가중치가 사용된다는 것이다.

N = 2 # 미니배치 크기
H = 3 # 은닉 상태 벡터의 차원 수
T = 20 # 시계열 데이터의 길이

dh = np.ones((N, H))
np.random.seed(3) # 재현할 수 있도록 난수의 시드 고정
Wh = np.random.randn(H, H)

norm_list = []
for t in range(T):
    dh = np.matmul(dh, Wh.T)
    norm = np.sqrt(np.sum(dh**2)) / N
    norm_list.append(norm)

print(norm_list)

의 결과는 다음과 같다.

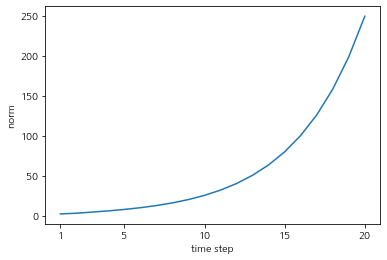
보듯 기울기의 크기가 급격히 증가하여 Gradient exploding이 발생한다. 이런 기울기 폭발이 일어나면 결국 오버플로를 일으켜 NaN(Not a Number)값을 발생시킨다.

반대로 초깃값에 0.5를 곱하여 변경해주면

Wh = np.random.randn(H, H) * 0.5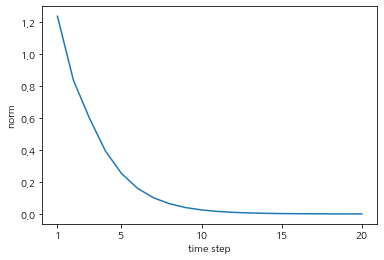

기울기가 급격히 감소하여 Gradient vanishing이 발생한다. 이로 인해 가중치 매개변수가 더 이상 갱신되지 않는다.

기울기 폭발 대책

기울기 폭발의 대책으로는 기울기 클리핑이라는 기법이 있다.

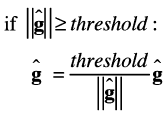
• 모든 매개변수에 대해 하나의 기울기로 처리한다고 가정하고, 이를 g^로 표기한다.
• threshold값을 문턱값으로 설정한다.
• 기울기의 L2노름 ||g^|| 이 문턱값 초과시 기울기를 수정한다.

g^는 예시로 W1과 W2 매개변수를 사용하는 모델이 있으면, 두 매개변수에 대한 기울기 dW1과 dW2를 결합한 것을 말한다.

dW1 = np.random.rand(3, 3) * 10
dW2 = np.random.rand(3, 3) * 10
grads = [dW1, dW2]
max_norm = 5.0

def clip_grads(grads, max_norm):
    norm_list = []
    total_norm = 0
    for grad in grads:
        total_norm += np.sum(grad ** 2)
    total_norm = np.sqrt(total_norm)
    
    rate = max_norm / (total_norm + 1e-6)
    if rate < 1:
        for grad in grads:
            grad *= rate
    

print('before:', dW1.flatten())
clip_grads(grads, max_norm)
print('after', dW1.flatten())

>>> before: [6.49144048 2.78487283 6.76254902 5.90862817 0.23981882 5.58854088
 2.59252447 4.15101197 2.83525082]
after [1.49503731 0.64138134 1.55747605 1.36081038 0.05523244 1.28709139
 0.59708178 0.95601551 0.65298384]

기울기 소실과 LSTM

기울기 소실을 막기 위해 기존 RNN에서 게이트가 추가된 LSTM과 GRU가 있다. 지금부터 LSTM에 집중해서 구조를 살펴 본다.

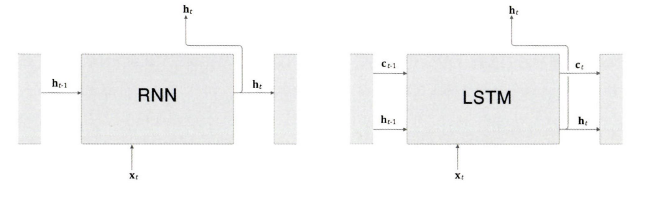
LSTM 계층의 인터페이스에는 c라는 경로가 있다. c를 기억 셀이라고 한다.

기억 셀의 특징은 데이터를 LSTM 계층 내에서만 주고 받는다는 것이다. 다른 계층으로는 출력하지 않는다는 것이다.

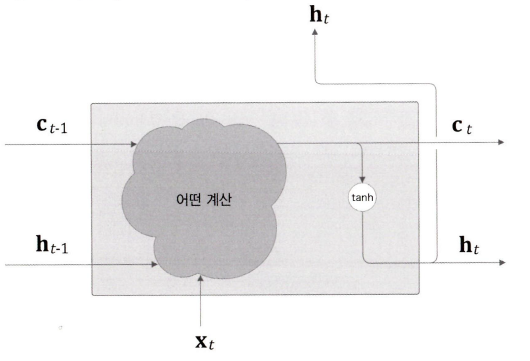
Ct을 사용해 은닉상태 ht를 구한다.
계산은 ht= tanh(ct)인데, 이는 Ct의 각 요소에 tanh 함수를 적용한다.

게이트의 역할

앞으로 게이트를 사용하여, 위의 그림 처럼 데이터의 흐름을 제어한다.

여기서 중요한 것은 '게이트를 얼마나 열까'라는 것도 데이터로부터 (자동으로) 학습한다.

게이트는 게이트의 열림 상태를 제어하기 위해서 전용 가중치 매개변수를 이용하여, 이 가중치 매개변수는 학습 데이터로부터 갱신된다. 참고로, 게이트의 열림 상태를 구할 때는 시그모이드 함수를 사용하는데, 시그모이드의 함수의 출력이 마침 0.0~1.0 사이의 실수이기 때문이다.

output 게이트

tanh(Ct)에 게이트를 적용하는 것을 생각해보자.

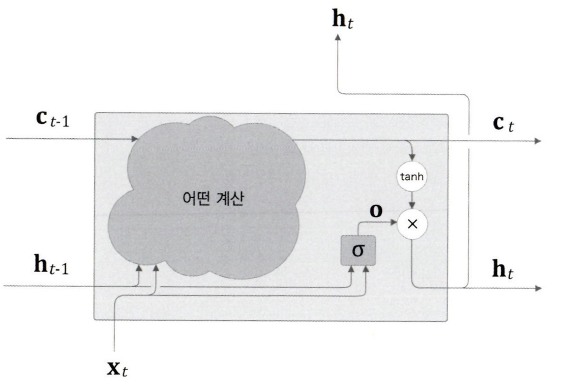
tanh(Ct)는 각 원소에 대해'그것이 다음 시각의 은닉 상태에 얼마나 중요한가'를 조정한다., 한편 이 게이트는 다음 은닉 상태 ht의 출력을 담당하는 게이트이므로 output 게이트(출력 게이트)라고 한다.

output 게이트의 열림 상태는 입력Xt와 이전 상태 ht-1로부터 구한다.

• 가중치 매개변수와 편향에는 output의 첫 글자인 o를 첨자로 추가한다.

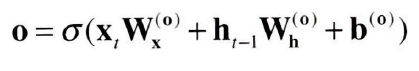
ht는 o와 tanh(Ct)의 곱으로 계산된다. 여기서 말하는 '곱'이란 원소별 곱이며, 이것을 아다마르 곱이라고 한다.

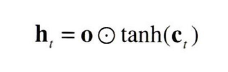
선형대수학에서, 아다마르 곱(영어: Hadamard product)은 같은 크기의 두 행렬의 각 성분을 곱하는 연산이다. 즉, 일반 행렬곱은 m x n과 n x p의 꼴의 두 행렬을 곱하지만, 아다마르 곱은 m x n 과 m x n의 꼴의 두 행렬을 곱한다.

forget 게이트

망각은 더 나은 전진을 낳는다. 말 그대로 forget, '무엇을 잊을까'를 명확하게 지시하는 것이다.

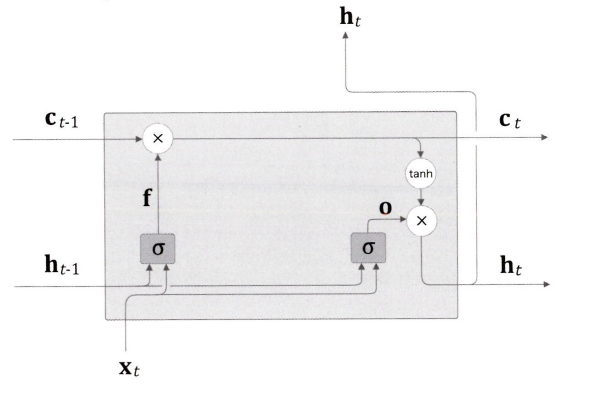
forget 게이트는 Ct-1의 기억 중에서 불필요한 기억을 잊게 해주는 게이트이다.

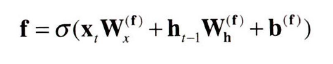
f를 구해서 ct = f⊙ct-1를 계산하면 된다.

새로운 기억 셀

forget으로 이전 시각의 기얼 셀로부터 잊어야 할 기억은 삭제 되었다. 그렇다면, 새로 기억해야 할 정보를 기억 셀에 추가해야 한다. 그림과 같이 tanh 노드를 추가한다.

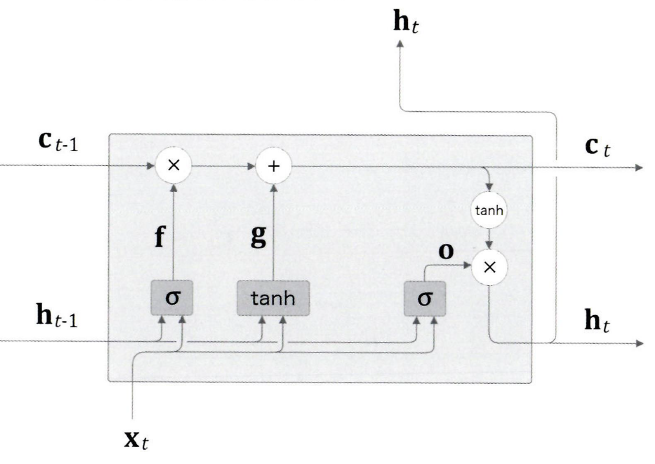
tanh 노드가 계산한 결과가 이전 시각의 기억 셀 Ct-1에 더해진다. 기억 셀의 새로운 '정보'가 추가 되는 것이다.

이 tanh노드는 '게이트'가 아니며, 새로운 '정보'를 기억 셀에 추가하는 것이 목적이다. 따라서 활성화 함수로는 시그모이드 함수가 아닌 tanh 함수가 사용된다.

tanh의 출력은 -1.0~1.0의 실수이다. 이 -1.0~1.0의 수치를 그 안에 인코딩된 '정보'의 강약(정도)을 표시한다고 해석할 수 있다.
한편 시그모이드 함수의 출력은 0.0~1.0의 실수이며, 데이터를 얼마만큼 통과시킬지를 정하는 비율을 뜻한다.
따라서 (주로) 게이트에서는 시그모이드 함수가, 실직적인 '정보'를 지나는 데이터에는 tanh 함수가 활성화 함수로 사용된다.

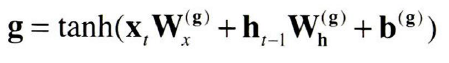
input 게이트

g에 게이트를 하나 추가해 보자. input 게이트는 g의 각 원소가 새로 추가되는 정보로써의 가치가 얼마나 큰지를 판단한다.(scaling)

마치 수도 꼭지 처럼 현재 정보에서 찬물 더운물을 적당히 조절해주는 역할을 한다. (f는 과거 정보에 대한 수도꼭지)

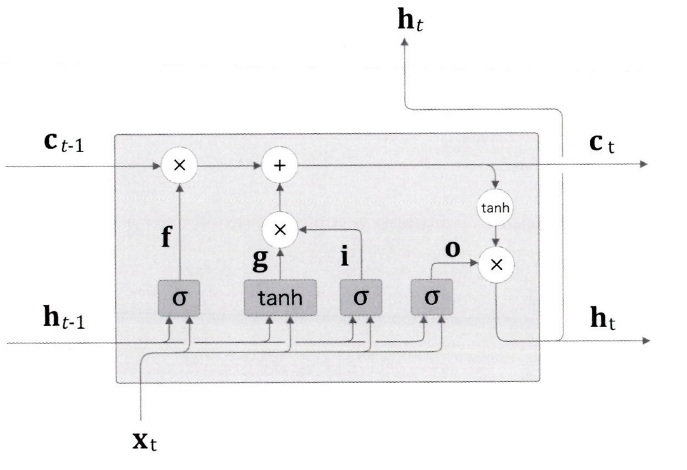
정보를 적절히 취사선택하는 것이 input 게이트의 역할이다.
input 게이트에 의해 가중된 정보가 새로 추가되는 셈이다.

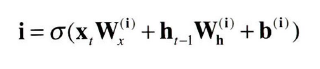
그 다음 i * g 를 구해서 기억 셀에 더하여 추가하면 된다.

LSTM 기울기 흐름

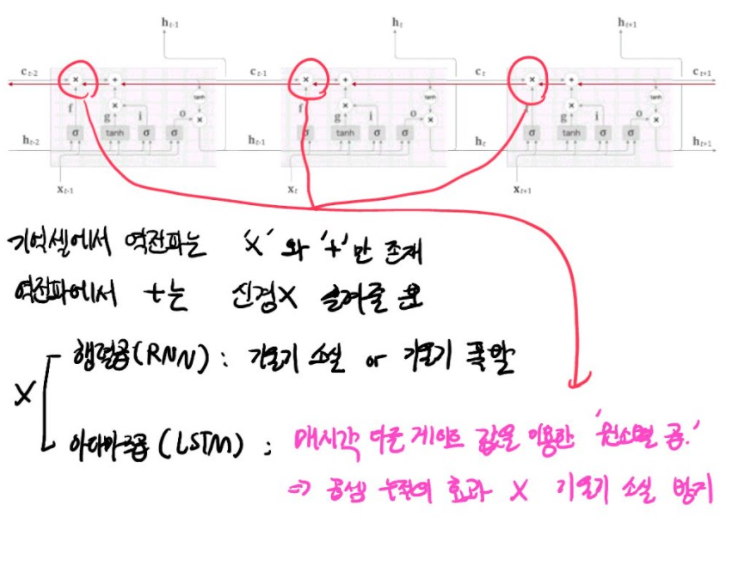
기억 셀의 역전파에서는 '+'와 'x'노드만을 지난다.

'+'노드는 상류에서 전해지는 기울기를 그대로 흘릴 뿐이다.

'x'노드는 '행렬 곱'이 아닌 '원소별 곱(아마다르 곱)'을 계산한다.

매 시각 다른 게이트 값을 이용해 원소별 곱을 계산한다.

매번 새로운 게이트 값을 이용하므로 곱셈의 효과가 누적되지 않아 기울기 소실이 일어나지 않는(혹은 일어나기 힘든) 것이다.

'x' 노드의 계산은 forget 게이트가 제어한다.

forget 게이트가 '잊어야 한다'고 판단한 기억 셀의 원소에 대해서는 그 기울기가 작아진다.

'잊어서는 안된다'라고 판단한 원소에 대해서는 기울기가 약화되지 않고 과거 방향으로 전해진다.

LSTM 구현

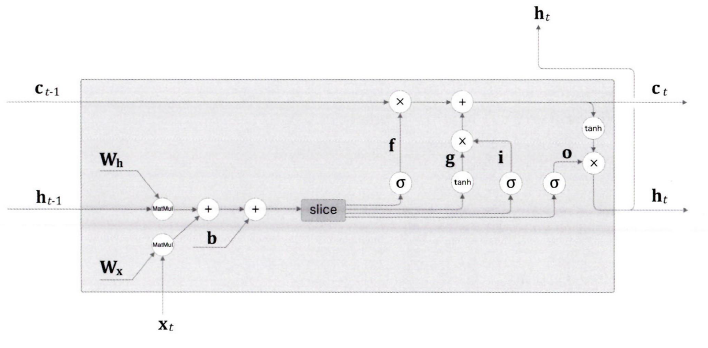
게이트에서 수행하는 계산을 정리한 수식이다.
주목할 점은 수식에 포함된 affine transformation이다.

• affine transformation - 행렬 변환과 평행 이동(편향)을 결합한 형태 xWx + hWh + b

이 덕분에 이 여러 식을 하나의 식으로 정리해 계산할 수 있다.

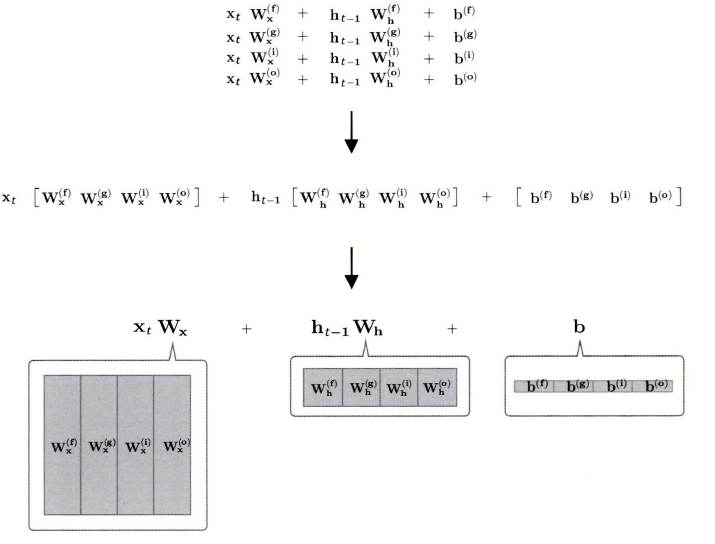
4번 계산할 것을 1회의 계산으로 끝마쳐 계산 속도가 빨라진다.

일반적으로 행렬 라이브러리는 '큰 행렬'을 한꺼번에 계산할 때가 각각을 계산할 때보다 빠르기 때문이다.

class LSTM:
    def __init(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

가중치(와 편향)에는 4개분의 가중치가 담겨 있다.

def forward(self, x, h_prev, c_prev):
        # Wx = (D, 4H), Wh = (H, 4H)
        Wx, Wh, b = self.params
        N, H = h_prev.shape
        
        A = np.matmul(x, Wx) + np.matmul(h_prev, Wh) + b
        
        # slice
        f = A[:, :H]
        g = A[:, H:2*H]
        i = A[:, 2*H:3*H]
        o = A[:, 3*H:]
        
        f = sigmoid(f)
        g = np.tanh(g)
        i = sigmoid(i)
        o = sigmoid(o)
        
        c_next = f * c_prev + g * i
        h_next = o * np.tanh(c_next)
        
        self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
        return h_next, c_next

forward

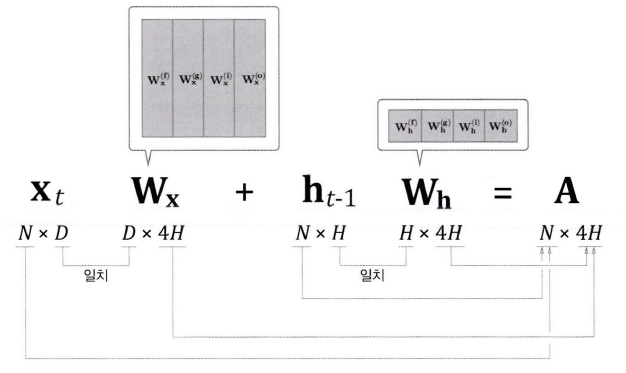
• 미니배치 수 N
• 입력 데이터의 차원 수 D
• 기억 셀과 은닉 상태의 차원 수 H
• 계산 결과 A에는 네 개분의 아핀 변환 결과 저장

forward의 형상은 이러한데, 이를 계산하여 Slice해서 각 연산 노드에 분배한다.

LSTM과 RNN의 매개변수 수는 같지만, 형상이 다르다.

def backward(self, dh_next, dc_next):
        Wx, Wh, b = self.params
        x, h_prev, c_prev, i, f, g, o, c_next = self.cache
        
        tanh_c_next = np.tanh(c_next)
        ds = dc_next + (o * dh_next) * (1 - tanh_c_next ** 2)
        
        dc_prev = ds * f
        
        di = ds * g
        df = ds * c_prev
        do = dh_next * tanh_c_next
        dg = ds * i
        
        # sigmoid
        di *= i * (1 - i)
        df *= f * (1 - f)
        do *= o * (1 - o)
        dg *= (1 - g ** 2 )
        
        dA = np.hstack((df, dg, di, do))
        
        dWh = np.dot(h_prev.T, dA)
        dWx = np.dot(x.T, dA)
        db = dA.sum(axis=0)
        
        self.grads[0][...] = dWx
        self.grads[1][...] = dWh
        self.grads[2][...] = db

        dx = np.dot(dA, Wx.T)
        dh_prev = np.dot(dA, Wh.T)

        return dx, dh_prev, dc_prev

backward

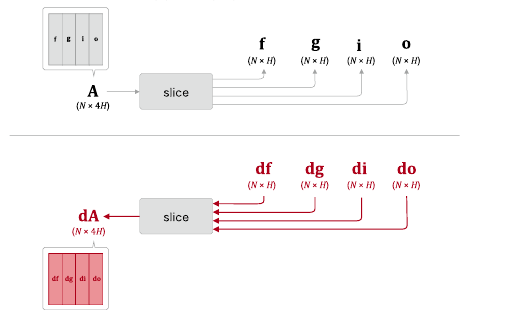
df, dg, di, do를 연결해서 dA를 만드는 것이다.
넘파이로 수행하려면

# np.hstack -> 가로로 연결
dA = np.hstack((df, dg, di, do)) # 역전파 4개의 기울기

을 사용하면 된다.

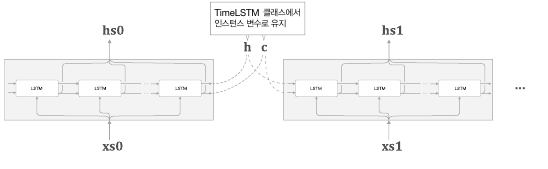
Time LSTM 구현

Time LSTM은 T개분의 시계열 데이터를 한꺼번에 처리하는 계층이다.

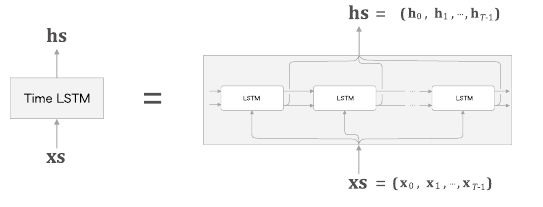
역시 학습할 때 Truncated BPTT를 사용해 역전파의 연결 길이를 끊는다.

class TimeLSTM:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None
        self.h, self.c = None, None
        self.dh = None
        self.stateful = stateful
        
    def forward(self, xs):
        Wx, Wh, b = self.params
        self.dh = None
        H = Wh.shape[0]
        
        self.layers = []
        hs = np.empty((N, T, H), dtpye = 'f')
        
        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')
        if not self.stateful or self.c is None:
            self.c = np.zeros((N, H), dtype='f')
            
        for t in range(T):
            layer = LSTM(*self.params)
            self.h, self.c = layer.forward(xs[:, t, :], self.h, self.c)
            hs[:, t, :] = self.h
            
            self.layers.append(layer)
        
        return hs
    
    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D = Wx.shape[0]
        
        dxs = np.empty((N, T, D), dtype='f')
        dh, dc = 0, 0
        
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            dx, dh, dc = layer.backward(dhs[:, t, :]+ dh, dc)
            dxs[:, t, :] = dx
            for i, grad in enumerate(layer.grads):
                grads[i] += grad
                
        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
            self.dh = dh
            return dxs
        
    def set_state(self, h, c=None):
        self.h, self.c = h, c
    
    def reset_state(self):
        self.h, self.c = None, None

다음장은 LSTM을 사용한 언어 모델에 대해서 공부해 보겠다..!

정리

• RNN은 gradient vanishing이나 exploded에 너무 sensitive하다.
• LSTM은 기존 RNN에 여러 제어를 위해 과거정보(forget)이나 현재정보(input)를 적절히 수도꼭지 처럼 찬물 더운물을 적당히 조절해주는 역할을 한다.
• LSTM의 기억 셀의 특징은 데이터를 LSTM 계층 내에서만 주고 받는다는 것이다. 다른 계층으로는 출력하지 않는다는 것이다.
• 역전파 시 행렬곱이 아닌 아다마르 곱을 통해서 곱셈의 효과가 누적되지 않아 기울기 소실이 일어나지 않는(혹은 일어나기 힘든)다.