위 주제는 밑바닥부터 시작하는 딥러닝2 8강, CS224d를 바탕으로 작성한 글 입니다.

이전글에서 Seq2seq 구현과 개선할 수 있는 기법 중에 입력 데이터 반전(Reverse)과 엿보기(Peeky)를 공부해봤다.
오늘은 "어텐션(Attention)"을 공부해 볼 것이다.
어텐션은 딥러닝 분야에서 틀림없이 중요한 기술중에 하나이다.

어텐션의 구조

이전 글에서 배웠던 Seq2seq구조에서 Encoder와 Decoder를 기억할 것이다.
이 구조에서 어텐션 메커니즘을 사용하여 한층 더 강력해진 모델을 만들어보자.

"Attention"말그대로 필요한 정보에만 '주목'할 수 있도록 하는 것을 의미한다.

seq2seq의 문제점

seq2seq에서는 Encoder가 시계열 데이터를 인코딩한다. 그리고 인코딩된 정보를 Decoder로 전달한다.
중요한 것은 'Encoder'의 출력은 '고정 길이의 벡터'인데, 이게 문제점이 있다는 것이다.

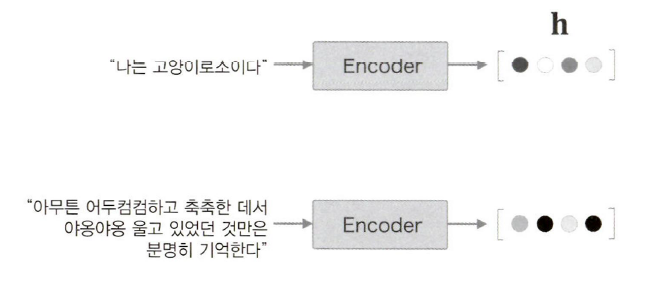
아무리 긴 문장이더라도 '고정 길이의 벡터'로 변환을 하기 때문에, 필요한 정보를 벡터에 다 담을 수 없는 상황이 생긴다.

Encoder 개선

그렇다면 Encoder에서 입력 문장의 길이에 따라 바꿔주는게 좋지 않을까?

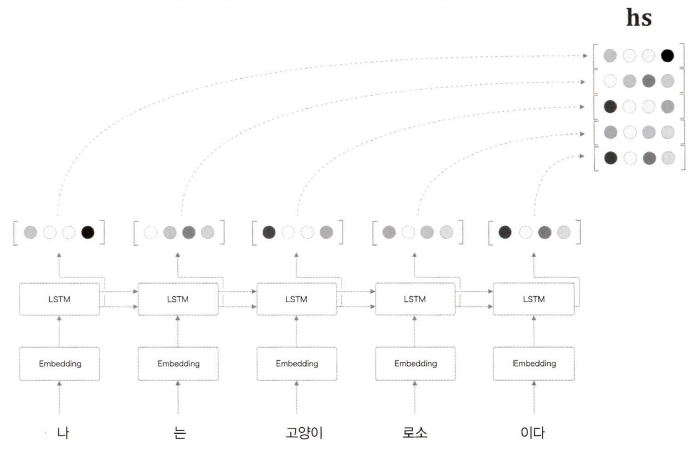
이전에는 마지막 은닉상태에 대한 벡터를 사용했지만, 그림처럼 각 시각(각 단어)의 은닉 상태 벡터를 모두 이용하면 입력된 단어와 같은 수의 벡터를 얻을 수 있다.

그림 처럼 5개의 벡터를 Encoder에서 출력하면, '하나의 고정 길이 벡터'라는 제약으로부터 해방이 된다.

많은 딥러닝 프레임워크(Tensorflow, Pytorch 등)에서는 RNN 계층 (LSTM, GRU 포함)을 초기화할 때, '모든 시각의 은닉 상태 벡터 반환'과 '마지막 은닉 상태 벡터만 반환'중 선택할 수 있다.
케라스를 예로 들면, RNN 계층의 초기화 인수로 return_sequences=True로 설정하면 모든 시각의 은닉 상태 벡터를 반환한다.

그렇다면 각 은닉 상태의 '내용'은 어떤 정보가 담겨 있을까?

분명한 것은 각 시각의 은닉 상태에서는 직전에 입력된 단어에 대한 정보가 많이 포함되어 있다는 사실이다.

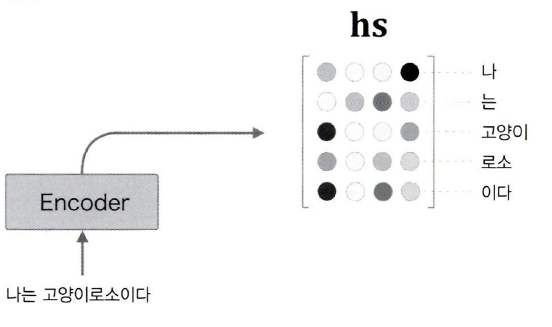
예로, "고양이" 단어를 입력했을 때의 LSTM 계층의 출력(은닉 상태)은 직전에 입력한 "고양이"라는 단어의 영향을 가장 크게 받는다.
따라서 이 은닉 상태 벡터는 "고양이"의 성분이 많이 들어간 벡터라고 생각할 수 있다.

그렇다면 Encoder가 출력하는 hs행렬은 각 단어에 해당하는 벡터들의 집합이라 볼 수 있다.

Decoder 개선 ①

그렇다면 Encoder에서 나오는 hs행렬을 Decoder가 어떻게 처리를 해야할까?

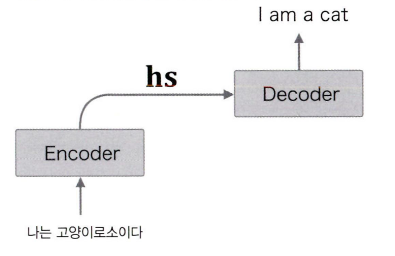
앞 장에서 본 가장 단순한 seq2seq에서는 Encoder의 LSTM의 '마지막'은닉 상태를 Decoder의 LSTM 계층의 '첫'은닉 상태로 설정한 것이다.
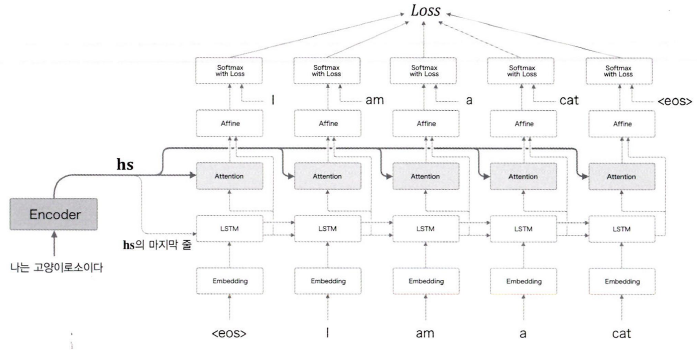
아래 그림은 어텐션 적용 전의 학습 시 디코더 구조이다.

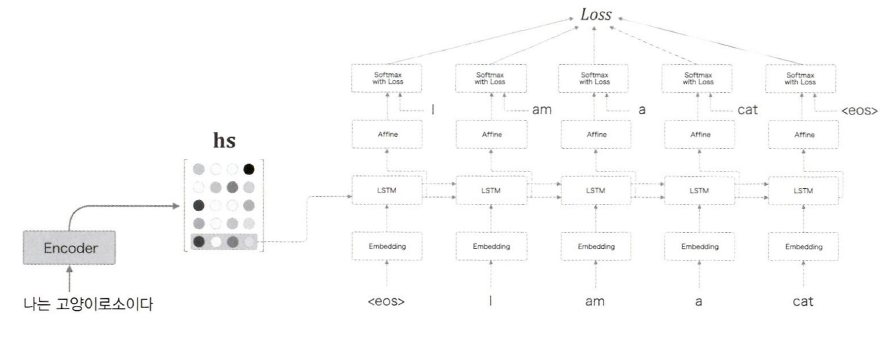
hs의 모든 벡터를 사용하여 디코더를 개선해보자.

우리가 문장을 번역할 때 머리 속에서 I=나, cat=고양이와 같이 어떤 단어에 주목(attention)하여 번역한다.
이와 같이 단어의 대응 관계를 나타내는 정보를 얼라인먼트(alignment)라고 한다. 지금까지는 얼라인먼트를 수작업으로 만들었는데, 어텐션 메커니즘을 활용하면 얼라인먼트를 자동으로 만들 수 있다.

한국어를 영어로 번역한다고 가정했을때, '특정 영어 단어'와 대응 관계가 있는 '특정 한국어 단어' 정보를 골라내는 것이 어텐션의 핵심 포인트이다.
다시 말해, 필요한 정보에 주목하여 그 정보로부터 문장 변환하는 것!

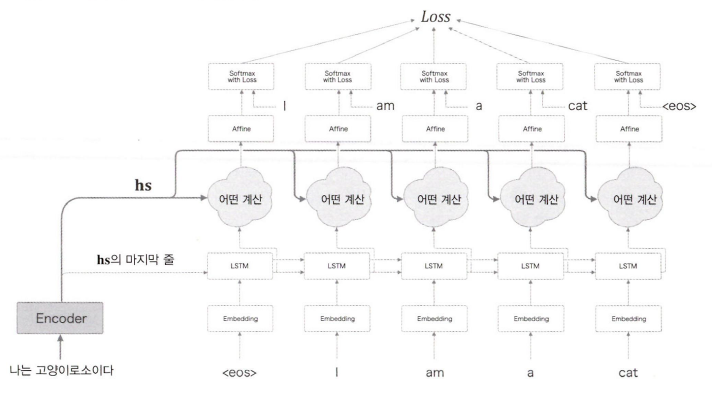
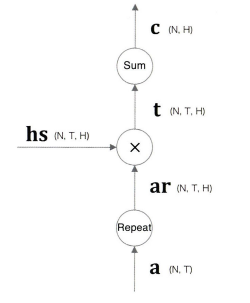
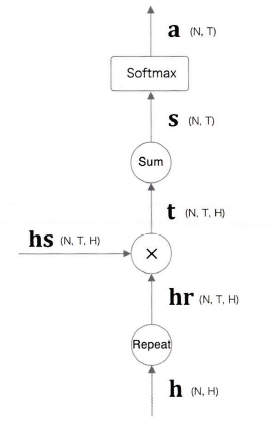
새롭게 추가되는 계층의 입력은 두 가지이다.

• Encoder로 부터 받는 hs
• 시각별 LSTM계층의 은닉 상태 h

여기서 필요한 정보만 골라 Affine 계층으로 출력한다.

참고로 지금까지와 똑같이 Encoder의 마지막 은닉 상태 벡터는 Decoder의 첫 번째 LSTM 계층에 전달한다.

여기서 우리가 하고 싶은 것은 단어들의 얼라인먼트를 추출하는 것이다. Decoder의 각 스텝에서 출력하고자 하는 단어와 대응 관계인 단어의 벡터를 hs에서 골라내겠다는 뜻이다.
예를 들어 디코더가 "I"를 출력할 때, hs에서 "나"에 대응하는 벡터를 선택한다.

문제는 선택하는 작업(여러 대상으로부터 몇 개를 선택하는 작업)은 미분할 수 없다는 점이다.

'선택한다'라는 작업을 미분 가능한 연산으로 하기 위해서는 '하나를 선택'하는 것이 아니라, '모든 것을 선택'한다는 것이다.
그리고 그림과 같이 각 단어의 중요도를 나타내는 '가중치'를 별도로 계산하도록 한다.

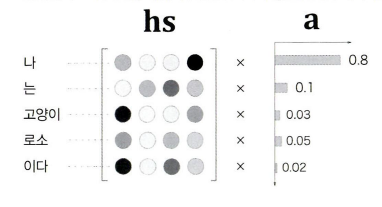
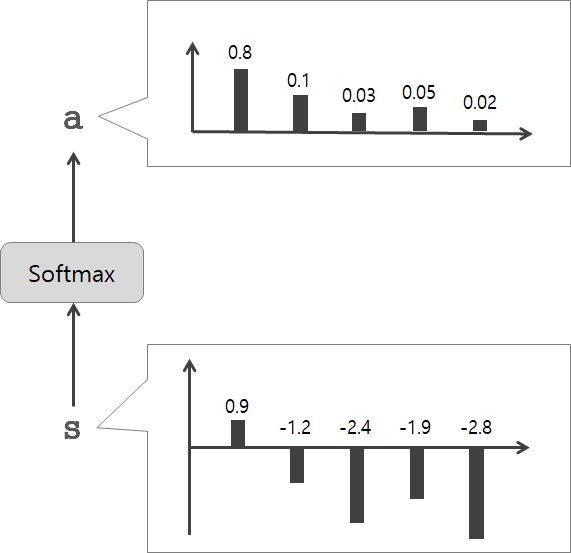
각 단어의 중요도를 나타내는 '가중치'(기호 a)를 이용한다.
a는 확률분포처럼 각 원소가 0.0 ~ 1.0 사이의 스칼라(단일 원소)이며, 모든 총합은 1이된다.
a와 hs로부터 가중합(weighted sum)을 구하여, 원하는 벡터를 얻는다.

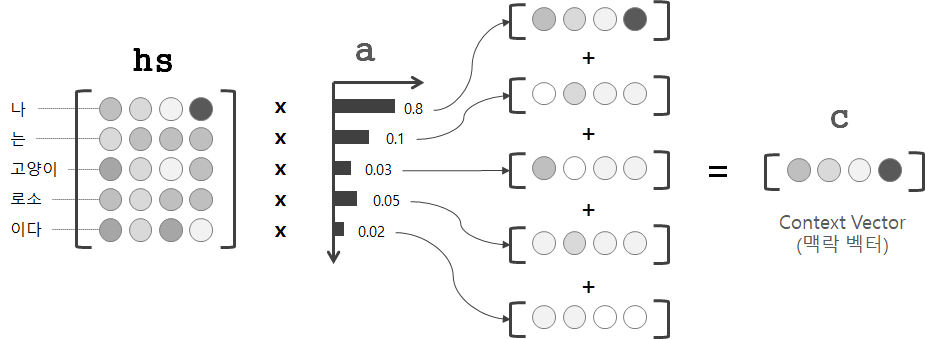
이를 '맥락 벡터'라고 부르고 기호 c로 표기를 한다.
그림에서는 맥락 벡터 c에 "나" 벡터의 성분이 많이 포함되어 있다는 것을 알 수 있다.
즉, "나"벡터를 '선택'하는 작업을 가중합으로 대체하고 있다는 것을 알 수 있다.

만약 가중치가 1이면 "나"벡터를 '선택'한다고 해석할 수 있다.
맥락 벡터 c에는 현 시각의 변환을 수행하는 데 필요한 정보가 담겨 있다. 그렇게 되도록 데이터로부터 학습한다는 것이다.

T, H = 5, 4
hs = np.random.randn(T, H)
a = np.array([0.8, 0.1, 0.03, 0.05, 0.02])

ar = a.reshape(5, 1).repeat(4, axis=1)
print(ar.shape)
# (5, 4)

t = hs * ar
print(t.shape)
# (5, 4)

c = np.sum(t, axis=0)
print(c.shape)
# (4,)

시계열의 길이를 T=5, 은닉 상태 벡터의 원소 수를 H=4로 하여 가중합을 구하는 것을 알 수 있다.
ar = a.reshape(5, 1).repeat(4, axis=1)는 (5, 1)로 reshape하고 asis=1로 4번 반복하여 (5, 4)의 배열을 생성한다.

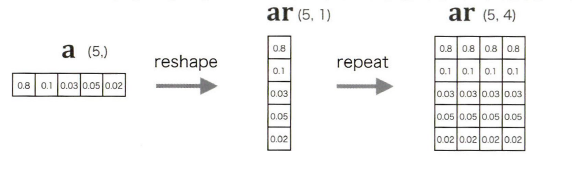
repeat() 대신에 넘파이의 브로드캐스트를 사용해도 된다. hs*ar로 해도 되는데, 하지만 복사가 된다는 점을 보이기 위해 repeat()메서드를 사용한다.

class WeightSum:
    def __init__(self):
        self.params, self.grads = [], []
        self.cache = None

    def forward(self, hs, a):
        N, T, H = hs.shape

        ar = a.reshape(N, T, 1)#.repeat(T, axis=1)
        t = hs * ar
        c = np.sum(t, axis=1)

        self.cache = (hs, ar)
        return c

    def backward(self, dc):
        hs, ar = self.cache
        N, T, H = hs.shape
        dt = dc.reshape(N, 1, H).repeat(T, axis=1)
        dar = dt * hs
        dhs = dt * ar
        da = np.sum(dar, axis=2)

        return dhs, da

미니배치 처리를 하여 만든 WeightSum 클래스 구현이다.
배열의 형상을 잘 살펴보면 repeat()와 sum()에서 어느 차원의 축을 지정할지를 알 수 있다.

Decoder 개선 ②

"근데 중요도를 나타내는 가중치a는 어떻게 구하는거지?" 라는 의문이 생길 것이다.
당연히 데이터로부터 자동으로 학습할 수 있도록 해야한다.

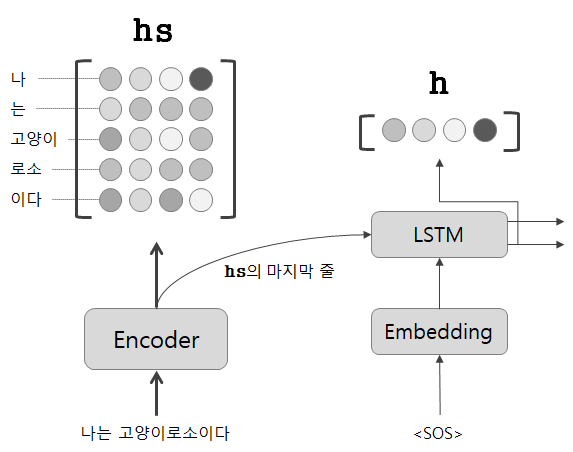
Decoder의 LSTM 계층의 은닉 상태 벡터를 h라 표기한다.

우리가 알고싶은 것은 h가 hs의 각 단어 벡터와 얼마나 비슷한지를 파악하는 것인데, 이 말은 Decoder의 입력 단어(ex. <sos>, I, am, a, cat 중 하나)와 대응되는 인코더의 입력 단어(ex. 나, 는, 고양이, 로소, 이다)가 무엇인지 파악하는 것이다.

간단하게 '내적'을 이용해 볼 수 있다.
벡터의 내적을 통해 두 벡터가 얼마나 유사한지 판단할 수 있다.
직관적으로 설명하면 내적을 통해 두 벡터가 얼마나 같은 방향을 향하고 있는지를 판단할 수 있는 것이다.

벡터의 유사도를 구하는 방법은 내적 외에도 작은 신경망을 사용하는 경우도 있다.

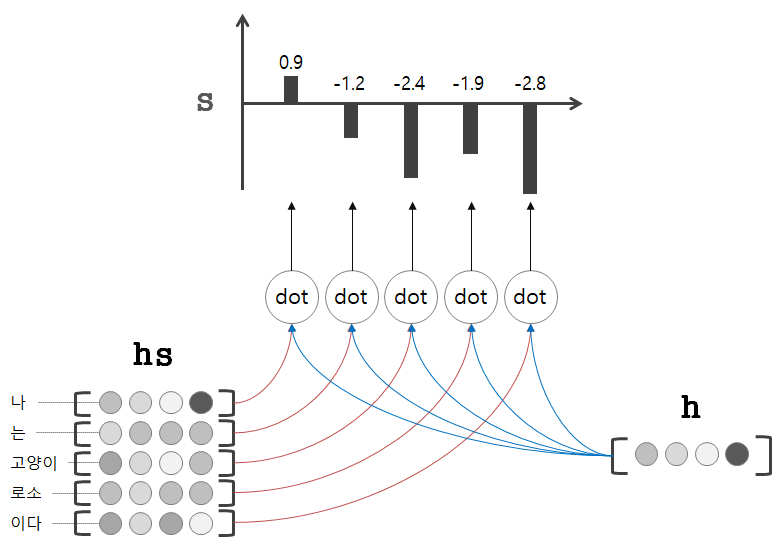
내적을 이용해 h와 hs의 각 단어 벡터와의 유사도를 구한다.
s는 그 결과인데, s는 정규화하기 전의 값이며, 'score'라고한다. 후에 Softmax로 정규화를 해준다.

class AttentionWeight:
    def __init__(self):
        self.params, self.grads = [], []
        self.softmax = Softmax()
        self.cache = None

    def forward(self, hs, h):
        N, T, H = hs.shape

        hr = h.reshape(N, 1, H)#.repeat(T, axis=1)
        t = hs * hr
        s = np.sum(t, axis=2)
        a = self.softmax.forward(s)

        self.cache = (hs, hr)
        return a

    def backward(self, da):
        hs, hr = self.cache
        N, T, H = hs.shape

        ds = self.softmax.backward(da)
        dt = ds.reshape(N, T, 1).repeat(H, axis=2)
        dhs = dt * hr
        dhr = dt * hs
        dh = np.sum(dhr, axis=1)

        return dhs, dh

Weight Sum 계층 처럼 Repeat과 Sum 연산이 등장한다.

역전파시 Repeat과 Sum은 반대로 해주면 된다.

Decoder 개선 ③

지금 까지 Decoder 개선안을 2개를 말했다.
1. Weight Sum
2. Attention Weight

이제 이 두 계층을 하나로 합쳐보자.

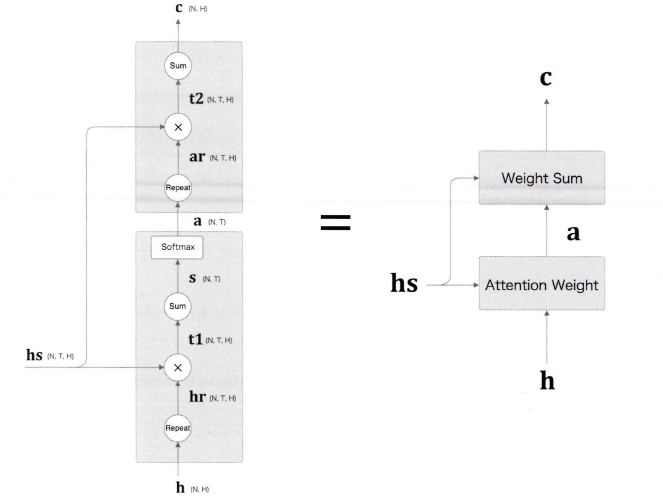
h: Decoder의 LSTM 계층이 출력한 은닉상태
hs: Encoder가 출력하는 각 단어에 대한 벡터
a: 가중치 벡터
c: 맥락 벡터

순서를 다시 설명하면

• Attention Weight 계층은 Encoder가 출력하는 각 단어의 벡터 hs에 주목하여 단어의 가중치 a를 구한다.
• Weight Sum 계층이 a와 hs의 가중합을 구하고, 그 결과를 맥락 벡터 c로 출력한다.

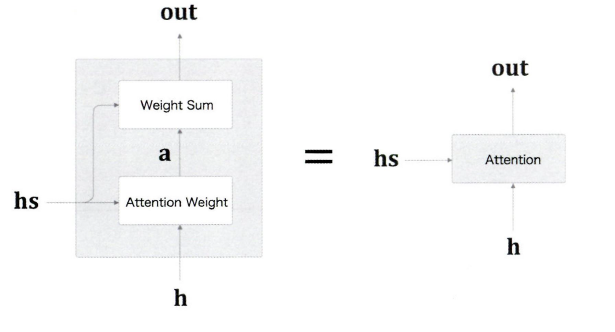
이 두가지를 합친 것을 Attention 계층이라고 한다.

class Attention:
    def __init__(self):
        self.params, self.grads = [], []
        self.attention_weight_layer = AttentionWeight()
        self.weight_sum_layer = WeightSum()
        self.attention_weight = None
        
    def forward(self, hs, h):
        a = self.attention_weight_layer.forward(hs, h)
        out = self.weight_sum_layer.forward(hs, a)
        self.attention_weight = a
        return out
    
    def backward(self, dout):
        dhs0, da = self.weight_sum_layer.backward(dout)
        dhs1, dh = self.attention_weight_layer.backward(da)
        dhs = dhs0 + dhs1
        return dhs, dh

forward에서 각 단어의 가중치를 나중에 참조할 수 있도록 attention_weight라는 인스턴스 변수에 a를 저장한다.

나머지는 단지 계층을 합치고 순전파와 역전파를 진행해주는 것이다. 코드는 아주 쉽게 이해할 수 있다는 것!

이렇게 만든 Attention 계층은 LSTM 계층과 Affine 계층 사이에 넣어주면 된다.

Decoder에 어텐션 정보를 '추가'할 수 있게 되었다.

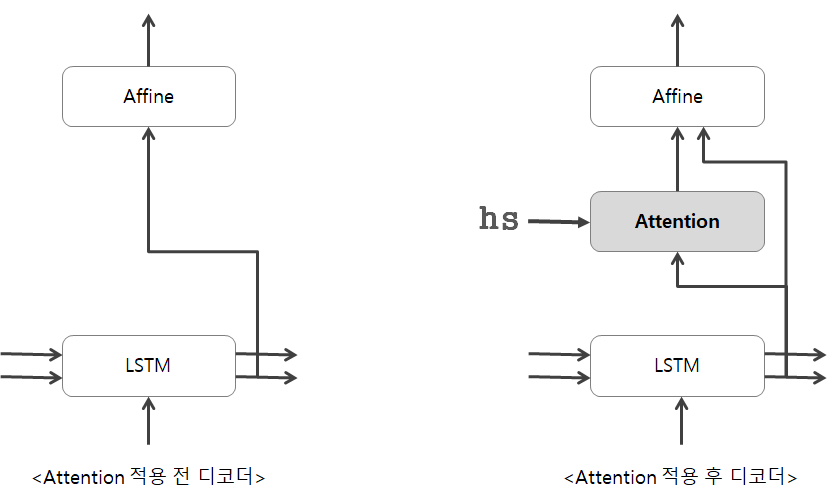
Affine 계층에는 기존과 마찬가지로 LSTM의 은닉 상태 벡터를 주고, 더해서 Attention 계층의 맥락 벡터까지 입력하는 것!

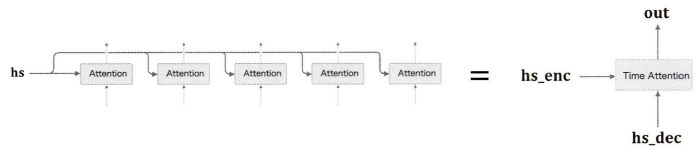
그러면 당연히 Time Attention도 구현할 수 있다.

class TimeAttention:
    def __init__(self):
        self.params, self.grads = [], []
        self.layers = None
        self.attention_weights = None

    def forward(self, hs_enc, hs_dec):
        N, T, H = hs_dec.shape
        out = np.empty_like(hs_dec)
        self.layers = []
        self.attention_weights = []

        for t in range(T):
            layer = Attention()
            out[:, t, :] = layer.forward(hs_enc, hs_dec[:,t,:])
            self.layers.append(layer)
            self.attention_weights.append(layer.attention_weight)

        return out

    def backward(self, dout):
        N, T, H = dout.shape
        dhs_enc = 0
        dhs_dec = np.empty_like(dout)

        for t in range(T):
            layer = self.layers[t]
            dhs, dh = layer.backward(dout[:, t, :])
            dhs_enc += dhs
            dhs_dec[:,t,:] = dh

        return dhs_enc, dhs_dec

Time 계층에 대해서는 너무 많이 말해서 생략한다.
간단하게만 말하자면 시계열 방향으로 펼쳐진 계층(T개)을 하나로 모아 블록형식으로 구현하면 된다.

Seq2seq + Attention

이제 Seq2seq에 적용해보자
구현할 Class는 AttentionEncoder, AttentionDecoder, AttentionSeq2seq이다.

AttentionEncoder

이전의 seq2seq는 Encoder의 forward()에서 LSTM의 마지막 은닉 상태 벡터만들 반환했었다.
그에 반해, 이번에는 모든 은닉 상태를 반환한다.

class AttentionEncoder(Encoder):
    def forward(self, xs):
        xs = self.embed.forward(xs)
        hs = self.lstm.forward(xs)
        return hs

    def backward(self, dhs):
        dout = self.lstm.backward(dhs)
        dout = self.embed.backward(dout)
        return dout

seq2seq는 hs[:, -1, :] 였지만 Attention을 추가하면 hs를 return하는 것을 알 수 있다.

AttentionDecoder

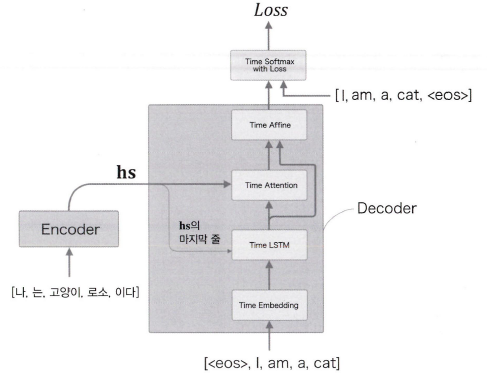
Decoder의 구현은 Softmax 계층 앞까지만 구현한다.

class AttentionDecoder:
   def __init__(self, vocab_size, wordvec_size, hidden_size):
       V, D, H = vocab_size, wordvec_size, hidden_size
       rn = np.random.randn

       embed_W = (rn(V, D) / 100).astype('f')
       lstm_Wx = (rn(D, 4 * H) / np.sqrt(D)).astype('f')
       lstm_Wh = (rn(H, 4 * H) / np.sqrt(H)).astype('f')
       lstm_b = np.zeros(4 * H).astype('f')
       affine_W = (rn(2*H, V) / np.sqrt(2*H)).astype('f')
       affine_b = np.zeros(V).astype('f')

       self.embed = TimeEmbedding(embed_W)
       self.lstm = TimeLSTM(lstm_Wx, lstm_Wh, lstm_b, stateful=True)
       self.attention = TimeAttention()
       self.affine = TimeAffine(affine_W, affine_b)
       layers = [self.embed, self.lstm, self.attention, self.affine]

       self.params, self.grads = [], []
       for layer in layers:
           self.params += layer.params
           self.grads += layer.grads

   def forward(self, xs, enc_hs):
       h = enc_hs[:,-1]
       self.lstm.set_state(h)

       out = self.embed.forward(xs)
       dec_hs = self.lstm.forward(out)
       c = self.attention.forward(enc_hs, dec_hs)
       out = np.concatenate((c, dec_hs), axis=2)
       score = self.affine.forward(out)

       return score

   def backward(self, dscore):
       dout = self.affine.backward(dscore)
       N, T, H2 = dout.shape
       H = H2 // 2

       dc, ddec_hs0 = dout[:,:,:H], dout[:,:,H:]
       denc_hs, ddec_hs1 = self.attention.backward(dc)
       ddec_hs = ddec_hs0 + ddec_hs1
       dout = self.lstm.backward(ddec_hs)
       dh = self.lstm.dh
       denc_hs[:, -1] += dh
       self.embed.backward(dout)

       return denc_hs

   def generate(self, enc_hs, start_id, sample_size):
       sampled = []
       sample_id = start_id
       h = enc_hs[:, -1]
       self.lstm.set_state(h)

       for _ in range(sample_size):
           x = np.array([sample_id]).reshape((1, 1))

           out = self.embed.forward(x)
           dec_hs = self.lstm.forward(out)
           c = self.attention.forward(enc_hs, dec_hs)
           out = np.concatenate((c, dec_hs), axis=2)
           score = self.affine.forward(out)

           sample_id = np.argmax(score.flatten())
           sampled.append(sample_id)

       return sampled

__init__

기존의 Decoder와 거의 비슷하다.

• affine_W 의 형태가 Attention 계층이 추가 됨으로써 2*H로 바뀌었다.
• TimeAttention()이 추가 되었다.

foward

• Time Attention의 순전파를 진행한다.
• Time Attention 계층의 출력과 LSTM 계층의 출력을 np.concatenate로 연결해준다.

backward

• backward도 기존과 많이 비슷한데, 합쳐진 출력을 backward하기 위해 H = H2 // 2로 나누어 주고 ddec_hs = ddec_hs0 + ddec_hs1로 Affine에 들어간 hs와 Attention에 들어간 hs를 더하여서 lstm.backward()를진행하면 된다.

generate

• generate도 기존과 똑같다. 단지 계층의 추가만 있을 뿐

AttentionSeq2seq

이것도 계층만 다르지, 전의 seq2seq구현과 코드가 같다.

class AttentionSeq2seq(Seq2seq):
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        args = vocab_size, wordvec_size, hidden_size
        self.encoder = AttentionEncoder(*args)
        self.decoder = AttentionDecoder(*args)
        self.softmax = TimeSoftmaxWithLoss()

        self.params = self.encoder.params + self.decoder.params
        self.grads = self.encoder.grads + self.decoder.grads

Attention 평가

한번 어텐션의 효과를 확인해보자.
"날짜 형식"을 변경하는 문제로 어텐션의 효과를 확인해본다.

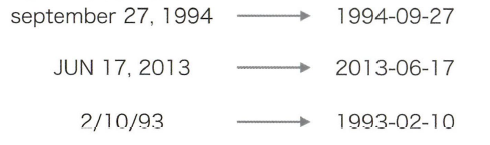
여러 가지 형식의 날짜 데이터를 "1994-09-27"처럼 같은 표준 형식으로 변환 할 것이다.

이 데이터의 특징은

• 다양한 변형이 존재하여 변환규칙이 복잡해 문제가 겉보기 만큼 간단하지 않다.
• 문제의 입력(질문)과 출력(답변) 사이에 "년-월-일"처럼 알기 쉬운 대응 관계가 있다.
  그래서 어텐션이 각각 원소에 올바르게 주목하고 있는지를 확인할 수 있다.

# 데이터 읽기
(x_train, t_train), (x_test, t_test) = sequence.load_data('date.txt')
char_to_id, id_to_char = sequence.get_vocab()

# 입력 문장 반전
x_train, x_test = x_train[:, ::-1], x_test[:, ::-1]

# 하이퍼파라미터 설정
vocab_size = len(char_to_id)
wordvec_size = 16
hidden_size = 256
batch_size = 128
max_epoch = 10
max_grad = 5.0

model = AttentionSeq2seq(vocab_size, wordvec_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)

acc_list = []
for epoch in range(max_epoch):
    trainer.fit(x_train, t_train, max_epoch=1,
               batch_size=batch_size, max_grad=max_grad)
    
    correct_num = 0
    for i in range(len(x_test)):
        question, correct = x_test[[i]], t_test[[i]]
        verbose = i < 10
        correct_num += eval_seq2seq(model, question, correct,
                                   id_to_char, verbose, is_reverse=True)
        
    acc = float(correct_num) / len(x_test)
    acc_list.append(acc)
    print('val acc %.3f%%' % (acc * 100))
    
model.save_params()

학습 코드도 계층의 차이, 데이터의 차이를 제외하고는 코드가 거의 같다.

• 에폭 2
  
• 에폭 10
  

오! 학습이 계속 될수록 val acc이 증가하다 100% acc 에 도달하는 것을 알 수 있다.

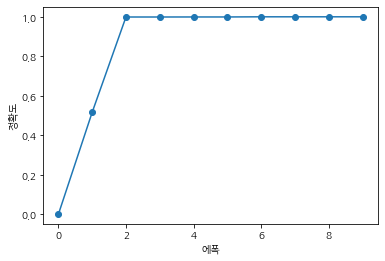
약 1~2에포크를 지날 때 acc값이 급 상승을 하는 것을 알 수 있다.

저번장의 모델인 peeky와 비교를 해보자

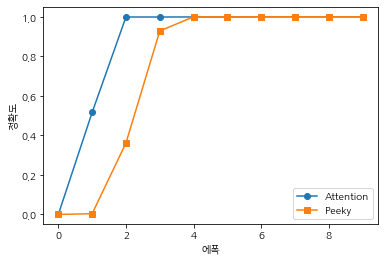
학습 속도는 확실히 Attention이 우세하다는 것을 알 수있다.
복잡하고 긴 시계열 데이터를 사용한다면, 학습속도 뿐아니라 정확도 측면에서도 어텐션이 유리하다.

시각화

시각화로 Attention이 어느 원소에 주의를 기울이는지를 볼 수 있다.
Attention 계층에서 attention_weight라는 인스턴스 변수에 가중치 a를 저장했던 것을 사용해 시각화를 하면 된다.

(x_train, t_train), (x_test, t_test) = \
    sequence.load_data('date.txt')
char_to_id, id_to_char = sequence.get_vocab()

# 입력 문장 반전
x_train, x_test = x_train[:, ::-1], x_test[:, ::-1]

vocab_size = len(char_to_id)
wordvec_size = 16
hidden_size = 256

model = AttentionSeq2seq(vocab_size, wordvec_size, hidden_size)
model.load_params()

_idx = 0
def visualize(attention_map, row_labels, column_labels):
    fig, ax = plt.subplots()
    ax.pcolor(attention_map, cmap=plt.cm.Greys_r, vmin=0.0, vmax=1.0)

    ax.patch.set_facecolor('black')
    ax.set_yticks(np.arange(attention_map.shape[0])+0.5, minor=False)
    ax.set_xticks(np.arange(attention_map.shape[1])+0.5, minor=False)
    ax.invert_yaxis()
    ax.set_xticklabels(row_labels, minor=False)
    ax.set_yticklabels(column_labels, minor=False)

    global _idx
    _idx += 1
    plt.show()


np.random.seed(1984)
for _ in range(5):
    idx = [np.random.randint(0, len(x_test))]
    x = x_test[idx]
    t = t_test[idx]

    model.forward(x, t)
    d = model.decoder.attention.attention_weights
    d = np.array(d)
    attention_map = d.reshape(d.shape[0], d.shape[2])

    # 출력하기 위해 반전
    attention_map = attention_map[:,::-1]
    x = x[:,::-1]

    row_labels = [id_to_char[i] for i in x[0]]
    column_labels = [id_to_char[i] for i in t[0]]
    column_labels = column_labels[1:]

    visualize(attention_map, row_labels, column_labels)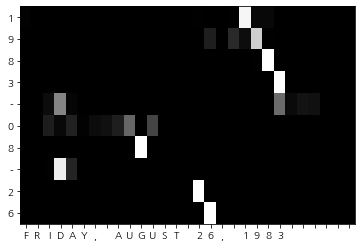

• 가로는 입력문장
• 세로는 출력 문장
• 각 맵의 원소는 밝을수록 값이 크다.

seq2seq가 "1"을 출력(세로)할 때에는 입력 문장의 "1"(가로)위치에 표시가 된다.

"1983"과 "26"이 훌륭하게 대응하고 있는게 보인다.

"08"은 심지어 "AUGUST"가 대응하고 있다는 것은 조금 놀랍다.

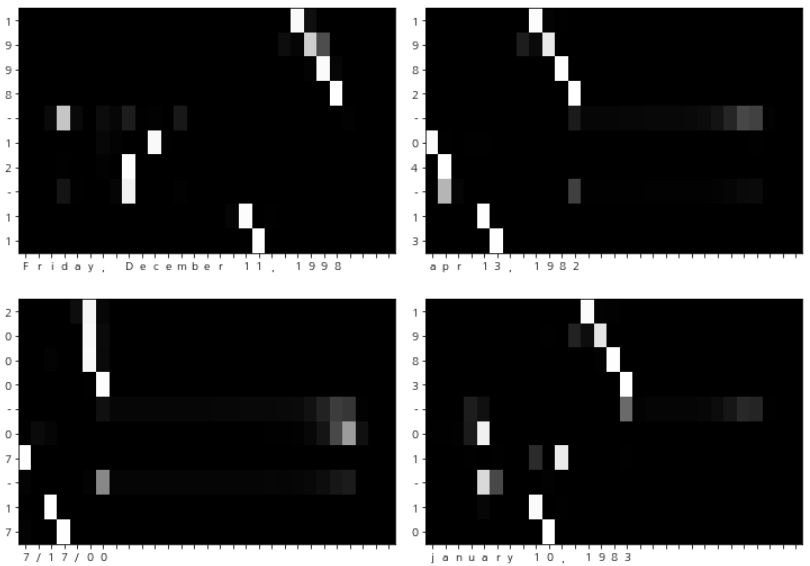
여러가지 결과이다.

원래 신경망 내부에서 어떠한 처리가 이루어 지는지는 이해할 수 없다. 반면 어텐션은 '인간이 이해할 수 있는 구조나 의미'를 모델에 제공한다.

다음장에서 어텐션에 관한 남은 이야기들이 계속된다...!