문제 정의
캘리포니아 인구조사 데이터를 사용해 캘리포니아의 주택 가격 예측 모델 만들기 → 특정 구역의 중간 주택 가격에 대한 예측
- 데이터의 각 샘플이 구역의 중간 주택 가격(레이블)을 가지고 있다. → 지도학습
- 값(중간 주택 가격) 예측 → 회귀
- 예측에 사용할 특성이 구역의 인구, 중간 소득 등 여러개이므로 다중 회귀 multiple regression
- 각 구역마다 하나의 값을 예측하므로 단변량 회귀 univariate regression
성능 측정 지표 선택
회귀 문제의 경우 전형적으로 평균 제곱근 오차 root mean square error (RMSE)를 성능 지표로 사용한다.

- X는 데이터셋에 있는 모든 샘플의 레이블을 제외한 모든 특성값을 포함하는 행렬
- h는 시스템의 예측 함수이며, 가설 hypothesis 이라고도 한다.
- RMSE(X, h)는 가설 h를 사용하여 일련의 샘플을 평가하는 비용 함수
cf) 이상치로 보이는 구역이 많은 경우, 성능 측정 지표로 평균 절대 오차 mean absolute error (MAE)를 사용할 수도 있다.
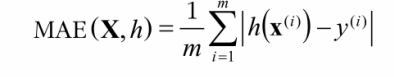
(RMSE와 MAE 모두 예측값의 벡터와 타깃값의 벡터 사이의 거리를 재는 방법)
데이터 다운로드
데이터 구조 훑어보기
housing = pd.read_csv('housing.csv')
housing.head()
DataFrame의 head() 메서드를 사용해 처음 다섯 행을 확인
- 각 행은 하나의 구역을 의미하며
- 10개의 feature를 갖는다.
('longitude', 'latitude', 'housing_median_age', 'total_rooms','total_bedrooms', 'population', 'households', 'median_income', 'median_house_value', 'ocean_proximity')
housing.info()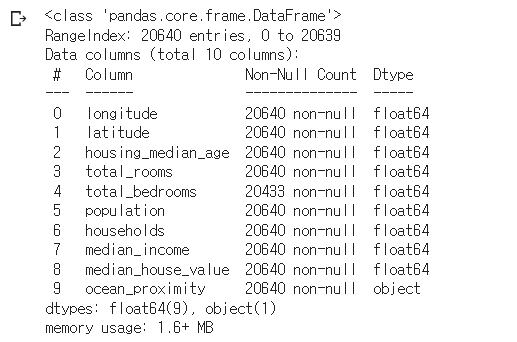
info() 메서드를 사용해 데이터에 대한 간략한 설명(전체 행 수, 각 특성의 데이터 타입과 null이 아닌 값의 개수) 확인
- 20,640개의 샘플이 들어있는 데이터셋
total_bedrooms특성은 20,433개만 null 값이 아님. → 207개의 구역은 이 특성을 가지고 있지 않다는 것을 의미ocean_proximity를 제외한 모든 특성은 숫자형 →value_counts()메서드를 통해 'ocean_proximity'에 어떤 카테고리가 있고, 각 카테고리마다 얼마나 많은 구역이 있는지 확인

housing.describe()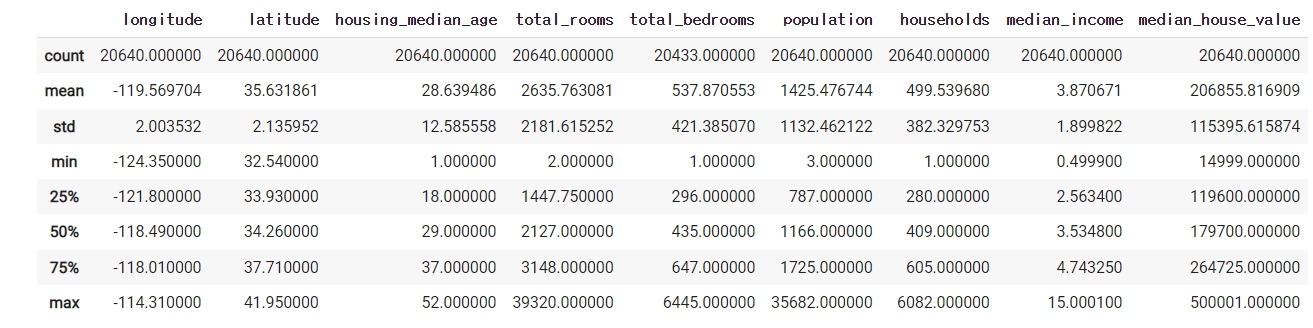
describe() 메서드를 통해 숫자형 feature의 요약 정보 확인 (null 값 제외)
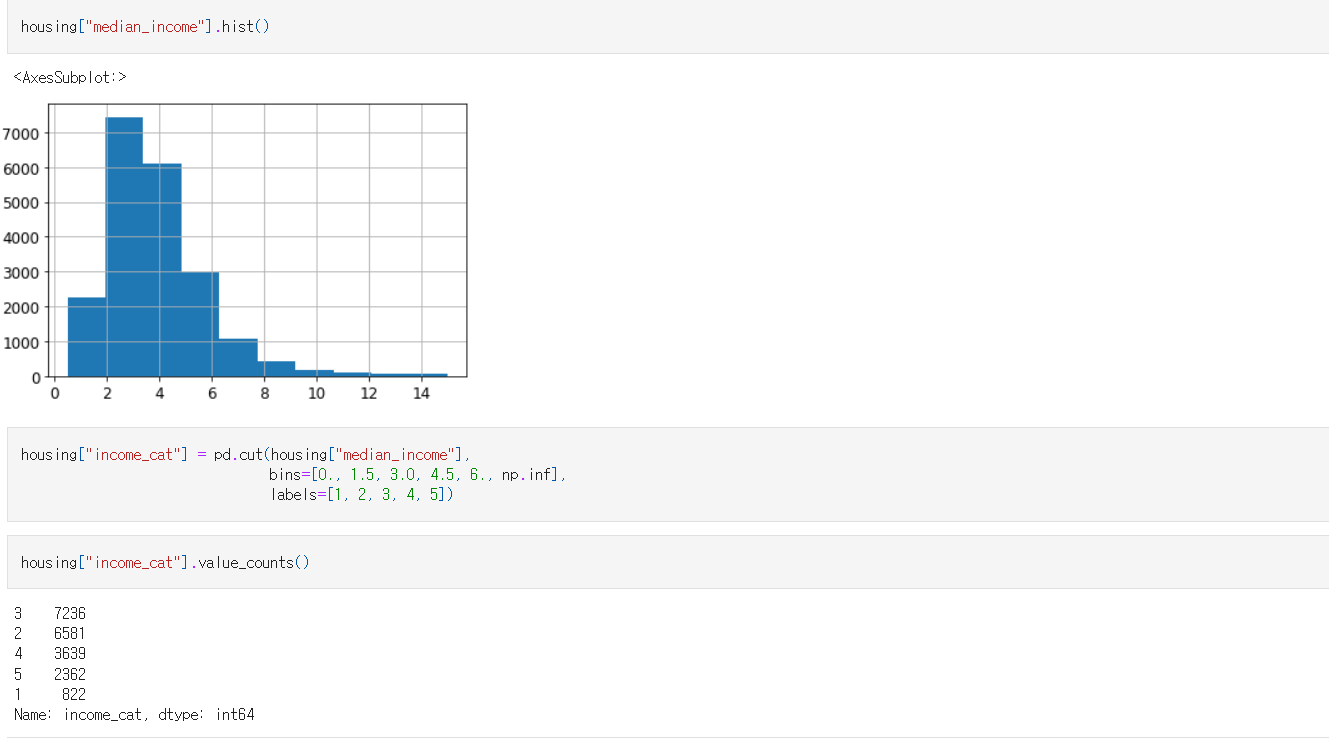
housing.hist(bins=50, figsize=(20, 15))
plt.show()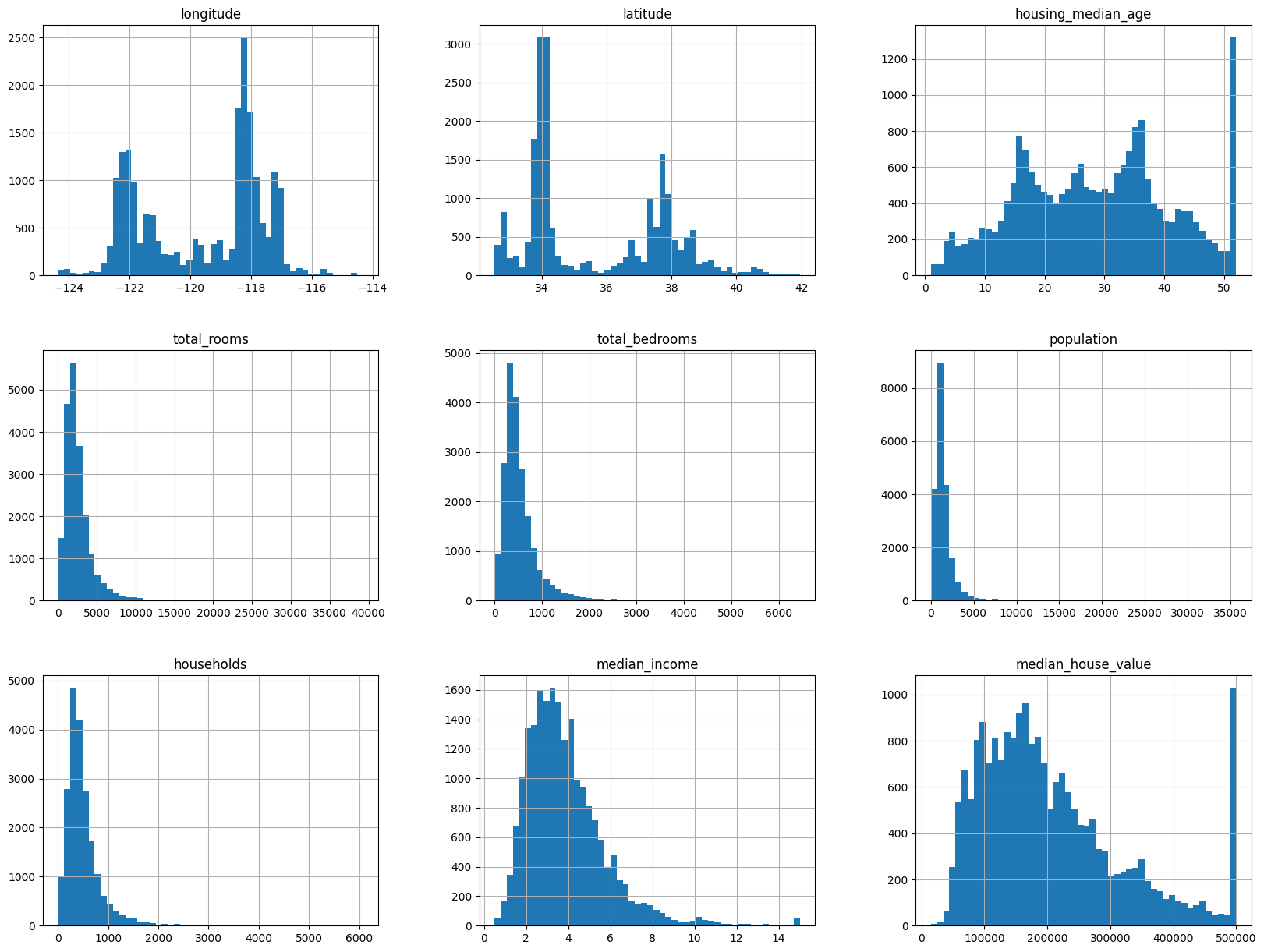
hist() 메서드를 호출하여 모든 숫자형 특성에 대한 히스토그램을 출력, 데이터의 형태를 파악한다.
housing_median_age와median_housing_value히스토그램은 오른쪽에서 그래프가 심하게 높아지면서 히스토그램이 끝나는 것으로 보아 마지막 값으로 한정되었음을 짐작할 수 있다.
test set 만들기
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)train_test_split함수 사용- 전체 데이터의 20%를 test dataset으로 생성한다.
random_state매개변수를 통해 난수 초깃값을 지정 → 실행 결과가 항상 동일하도록

참고) stratified sampling을 위한 코드
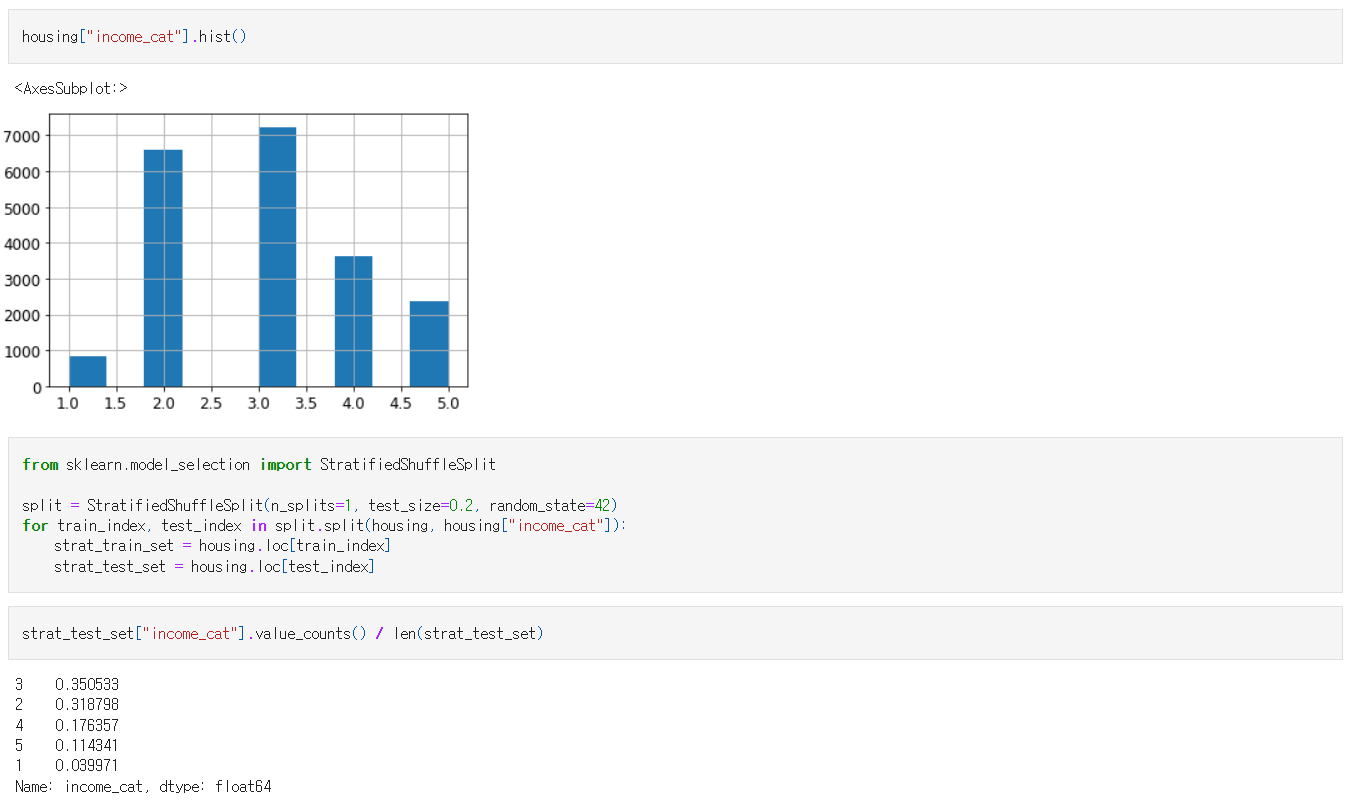
테스트 세트에서 소득 카테고리의 비율 확인
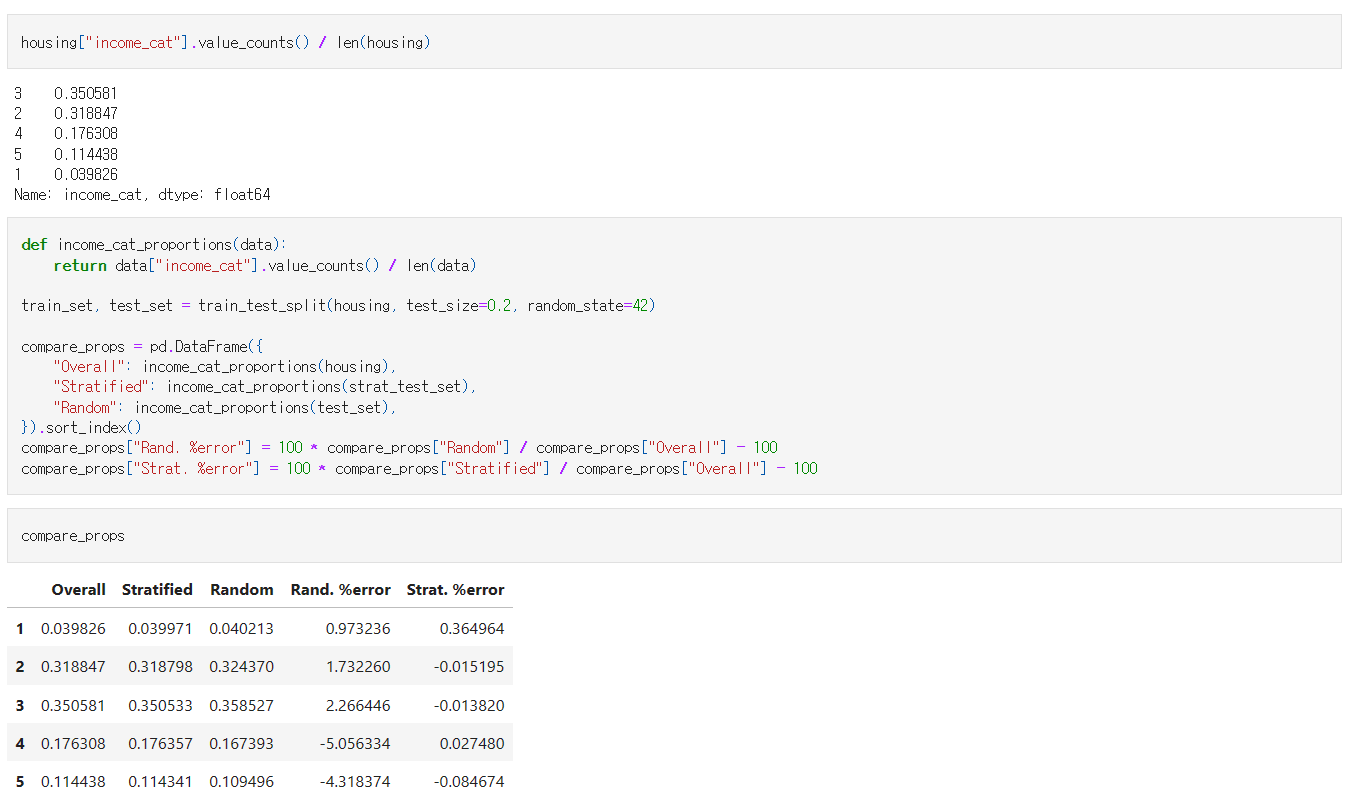
사이킷런의 StratifiedShuffleSplit 사용 → 계층 샘플링을 사용해 만든 테스트 세트가 전체 데이터셋의 소득 카테고리 비율과 거의 같은 것을 알 수 있다.

income_cat 특성을 삭제하여 데이터를 원래 상태로 되돌린다.
데이터 탐색과 시각화
housing = strat_train_set.copy()train 세트를 손상시키지 않기 위해 복사본을 만들어 사용한다.
데이터 시각화
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
- 주어진 지리 정보(위도, 경도)를 사용하여 모든 구역을 산점도로 만들어 데이터를 시각화한다.
alpha옵션을 0.1로 주어 데이터 포인트가 밀집된 영역을 확인할 수 있다.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()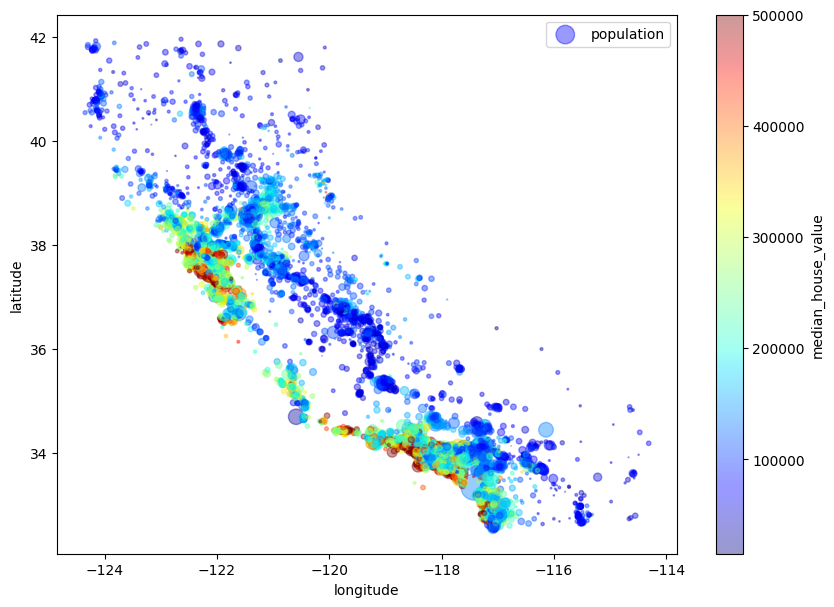
매개변수 조절
s: 원의 반지름은 구역의 인구를 나타냄c: 색상은 주택 가격을 나태냄
→ 빨간색은 높은 가격, 파란색은 낮은 가격, 큰 원은 인구가 밀집된 지역을 의미한다.
상관관계 조사
상관계수는 선형적인 상관관계(x가 증가하면 y는 증가하거나 감소)만 측정하며, 비선형적인 관계는 잡을 수 없다.
corr_matrix = housing.corr() corr() 메서드를 이용하여 계산한다.
corr_matrix["median_house_value"].sort_values(ascending=False)
중간 주택 가격과 다른 feature 사이의 상관관계를 확인한다.
- 상관관계의 범위는 -1부터 1까지
- 1에 가까울수록 강한 양의 상관관계를 가진다.
→median_house_value는median_income이 올라갈 때 증가하는 경향이 있다. - 계수가 -1에 가까우면 강한 음의 상관관계를 나타낸다.
→ 위도 latitude와 중간 주택 가격은 약한 음의 상관관계
(즉, 북쪽으로 갈수록 주택 가격이 조금씩 내려가는 경향이 있다.) - 계수가 0에 가까우면 선형적인 상관관계가 없다는 뜻
- 1에 가까울수록 강한 양의 상관관계를 가진다.
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))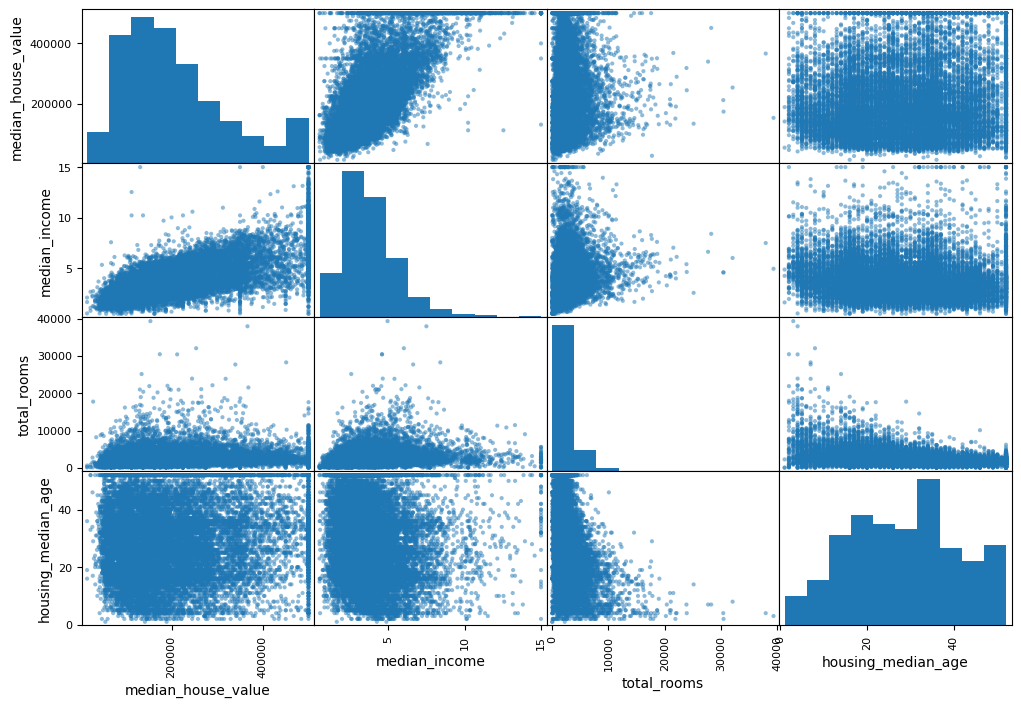
판다스의 scatter_matrix 함수를 사용하여 숫자형 특성 사이의 산점도를 그릴 수 있다.
(다른 수치형 특성에 대한 각 수치형 특성의 산점도와 히스토그램을 출력)
housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
plt.axis([0, 16, 0, 550000])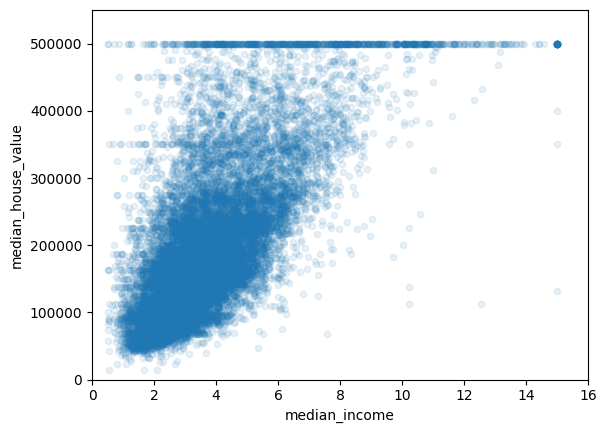
median_house_value와 median_income의 상관관계 산점도 확인
- 그래프가 위쪽으로 향하는 경향을 볼 수 있다.
- 가격 제한값이 $500,000에서 수평선으로 직선에 가까운 형태를 보인다.
( $450,000, $350,000, $280,000 근처에도 수평선이 보임 )
특성 조합으로 실험
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]가구당 방 개수, 가구당 인원 등 여러 특성의 조합을 시도해보고 다시 상관관계 행렬을 확인한다.
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)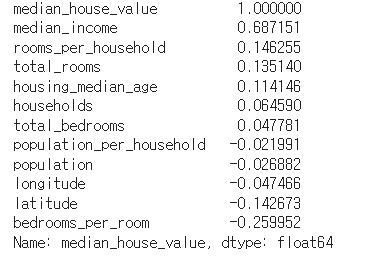
- bedrooms_per_room 특성은 전체 방 개수나 침실 개수보다 주택가격과의 상관관계가 높다.
머신러닝 알고리즘을 위한 데이터 준비
housing = strat_train_set.drop("median_house_value", axis=1) # 훈련 세트를 위해 레이블 삭제
housing_labels = strat_train_set["median_house_value"].copy()예측 변수와 레이블을 분리한다.
데이터 정제
-
일반적인 방법
-
housing.drop("total_bedrooms", axis=1)
→ 'total_bedrooms' 컬럼을 삭제한다. -
housing["total_bedrooms"].fillna(median, inplace=True)
→ 중간값을 계산하고 누락된 값을 이 값으로 채운다.
-
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")사이킷런의 SimpleImputer로도 누락된 값을 쉽게 다룰 수 있다. → 모든 수치형 특성의 누락된 값을 feature의 중간값으로 대체하는 객체 생성
housing_num = housing.drop("ocean_proximity", axis=1)중간값이 수치형 특성에서만 계산될 수 있기 때문에 텍스트 특성 'ocean_proximity'를 삭제한다.
imputer.fit(housing_num)각 특성의 중간값을 계산하여 그 결과를 객체의 statistics_ 속성에 저장
X = imputer.transform(housing_num)훈련 세트를 변환한다.
housing_tr = pd.DataFrame(X, columns=housing_num.columns, index=housing_num.index)
변환된 feature들이 들어있는 넘파이 배열을 다시 판다스 데이터프레임으로 되돌린다.
범주형 특성 다루기
범주형 입력 특성인 ocean_proximity 전처리
housing_cat = housing[["ocean_proximity"]]from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)사이킷런의 OneHotEncoder 클래스를 사용해 카테고리별 이진 특성을 만든다.
한 특성만 1이고 나머지는 0 → 원-핫 인코딩
출력은 희소행렬이며, 이는 수천 개의 카테고리가 있는 범주형 특성일 경우 매우 효율적이다.
feature scaling
머신러닝 알고리즘은 입력 숫자 feature들의 스케일이 많이 다른 경우 잘 작동하지 않는다.
( 주택 가격 데이터의 경우, 전체 방 개수의 범위는 6~39,320인 반면 중간 소득의 범위는 0~15이다.)
타깃값에 대한 스케일링은 일반적으로 필요하지 X
- min-max 스케일링
- 값이 0~1 범위에 들도록 스케일을 조정한다. ⇒ normalization
- 데이터에서 최솟값을 뺀 후 최댓값과 최솟값의 차이로 나누어 구할 수 있다.
- 사이킷런의
MinMaxScaler변환기를 이용할 수 있다.
(0~1 사이의 범위를 원하지 않는다면 feature_range 매개변수로 범위를 변경할 수 있다.)
- standardization
- 평균을 뺀 후 표준편차로 나누어 결과 분포의 분산이 1이 되도록 한다.
(min-max 스케일링과 달리 범위의 상한과 하한이 없어 어떤 알고리즘에서는 문제가 될 수 있다.) - 이상치에 영향을 덜 받는다.
- 사이킷런의
StandardScaler변환기를 이용
- 평균을 뺀 후 표준편차로 나누어 결과 분포의 분산이 1이 되도록 한다.
참고) 모든 변환기에서 스케일링은 test 세트가 포함된 전체 데이터가 아닌, train 데이터에 대해서만 fit() 메서드를 적용해야 한다. 그런 다음 train 세트와 test 세트, 새로운 데이터에 대해 transform() 메서드를 사용한다.
변환 파이프라인
col_names = "total_rooms", "total_bedrooms", "population", "households"
rooms_ix, bedrooms_ix, population_ix, households_ix = [
housing.columns.get_loc(c) for c in col_names] # 열 인덱스 구하기from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipeline.fit_transform(housing_num)from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)수치형과 범주형 feature를 전처리하는 과정을 하나의 파이프라인으로 만든다.
1.ColumnTransformer 클래스 임포트
2. 수치형 열 이름의 리스트와 범주형 열 이름의 리스트 만들기
3. ColumnTransformer 클래스 객체 만들기
(수치형 열은 num_pipeline을 사용해 변환되고, 범주형 열은 OneHotEncoder를 사용해 변환됨)
4. ColumnTransformer를 주택 데이터에 적용
model selection과 training
선형 회귀 모델
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("예측:", lin_reg.predict(some_data_prepared))
print("레이블:", list(some_labels))
train 세트의 몇 개의 샘플에 적용하여 실제값과 비교,
mean_square_error 함수를 사용해 전체 훈련 세트에 대한 RMSE 측정
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
DecisionTreeRegressor
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
오차 → 0
( 모델이 데이터에 너무 심하게 overfitting 된 것을 확인할 수 있다. )
교차 검증을 사용한 평가
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)train 세트를 fold라 불리는 10개의 서브셋으로 무작위 분할하고, 모델을 10번 훈련하고 평가한다.
(매번 다른 폴드를 선택해 평가에 사용하고 나머지 9개 폴드는 훈련에 사용)
def display_scores(scores):
print("점수:", scores)
print("평균:", scores.mean())
print("표준 편차:", scores.std())
print('DecisionTree')
print()
display_scores(tree_rmse_scores)
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
print('선형회귀모델')
print()
display_scores(lin_rmse_scores)
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(housing_prepared, housing_labels)housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmseforest_rmse 출력 : 18650.698705770003
from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
print('RandomForest')
print()
display_scores(forest_rmse_scores)
모델 세부 튜닝
그리드 탐색
하이퍼파라미터 조정 → 사이킷런의 GridSearchCV 사용
( 가능한 모든 하이퍼파라미터 조합에 대해 교차 검증을 사용해 평가한다. )
from sklearn.model_selection import GridSearchCV
param_grid = [
# 12(=3×4)개의 하이퍼파라미터 조합 시도
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
# bootstrap은 False로 하고 6(=2×3)개의 조합 시도
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor(random_state=42)
# 다섯 개의 폴드로 훈련, 총 (12+6)*5=90번의 훈련
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
RandomForestRegressor에 대한 최적의 하이퍼파라미터 조합을 탐색하는 코드
grid_search.best_params_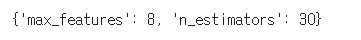
최상의 파라미터 조합을 확인할 수 있다.
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)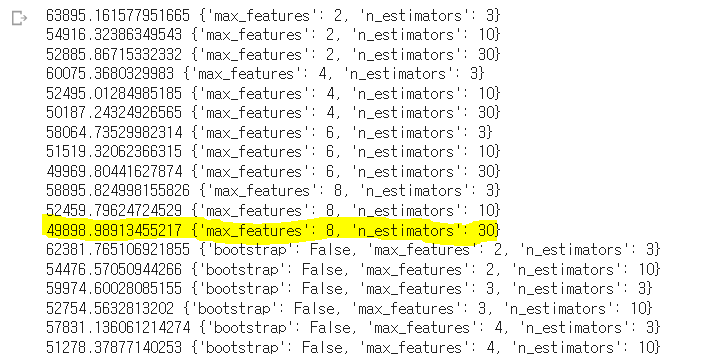
그리드서치에서 테스트한 하이퍼파라미터 조합의 점수를 확인할 수 있다.
랜덤 탐색
그리드 탐색 방법은 비교적 적은 수의 조합을 실행할 때 좋다.
하지만 하이퍼파라미터 탐색 공간이 커지면 RandomizedSearchCV를 사용하는 것이 더 좋다.
RandomizedSearchCV는 GridSearchCV와 거의 같은 방식으로 사용하지만, 가능한 모든 조합을 시도하는 대신 각 반복마다 하이퍼파라미터에 임의의 수를 대입하여 지정한 횟수만큼 평가한다.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=1, high=8),
}
forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
rnd_search.fit(housing_prepared, housing_labels)cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
테스트 세트로 시스템 평가하기
test dataset에서 최종 모델을 평가한다.
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse) # => 47,730.0 출력from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))
scipy.stats.t.interval()을 사용해 일반화 오차의 95% 신뢰 구간을 계산할 수 있다.