내용 정리 방법 설정
블로그에 일일이 코드를 적으며 설명을 적어두는 것은 귀찮아서 기본적으로 알고리즘이 어떻게 돌아가는 지만 정리하고 과제만 추가 한 후 실제로 어떻게 돌아가는지는 코렙에 주석으로 달아놓는 방법으로 설정하였다.
혼공머신 코드 정리
k-최근접 이웃 회귀
k-최근접 이웃 회귀란 k-최근접 분류와 비슷한데 다른 점은 수를 예측해야 한다는 점입니다. 이를 위해 x 값이 정해지면 근처에 있는 값들의 평균을 이용해 y값을 예측하는 그런 알고리즘 입니다. 모델을 만든 뒤 테스트 할 때에 결정계수를 사용해 모델의 성능을 평가한다.
결정계수 = 1 - {(타깃 - 예측)의 제곱의 합 / (타깃 - 평균)의 제곱의 합}
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input, train_target)선형 회귀
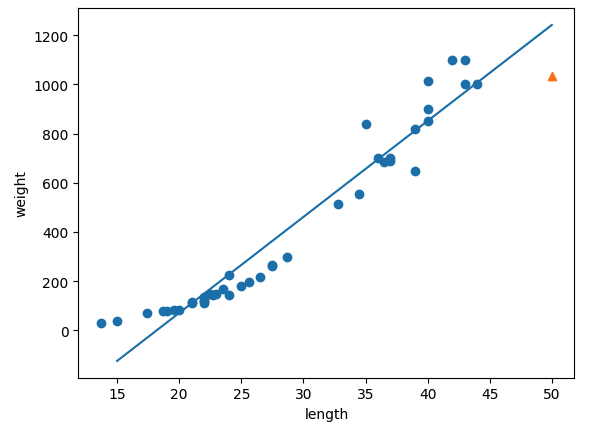
이번에 배운 선형 회귀는 1차항인 선형회귀와 다항 회귀를 학습 하였다. 특성이 한개인 선형 회귀의 경우 직선으로 표현되는데, 데이터들을 가장 잘 표현하는 직선을 그린 것이 선형 회귀라고 한다. (내가 기억하기로는 실제 값과 예측값의 거리가 가장 작게 되는 직선이었나..?) 다항 회귀는 여기서 계수를 추가하여 곡선의 형태로 데이터 예측을 하는 것이다.
선형회귀 모형
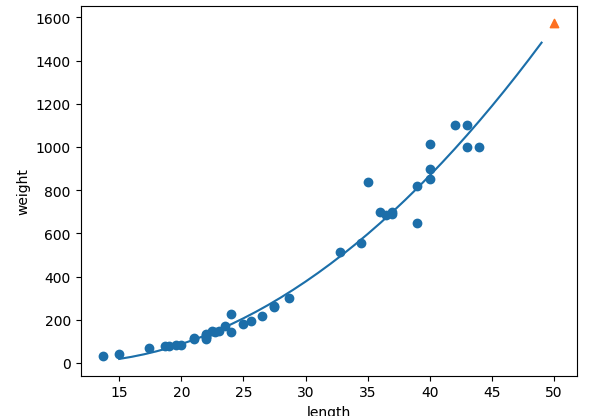
다항회귀 모형
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target)다중 회귀
다항 회귀와는 다른 계념으로 다항회귀는 특성을 늘릴 때에 하나의 값을 제곱하고, 세제곱 해서 만드는데, 다중회귀는 특성 자체가 여러가지 있는 회귀이다. 다중 회귀도 특성을 늘려서 모델을 만들면 좋은데, 특성들의 값끼리 곱하거나, 특성을 제곱하여 새로운 특성을 만들어준다.
# 사이킷런의 변환기를 이용하여 특성 추가 생성
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)그다음 선형회귀를 다항회귀에서 했던 것과 같이 하면 된다.
# 선형 회귀 모델 훈련
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)규제 (릿지와 라소)
선형 회귀 모델이 과대적합이 되는 경우 규제를 이용해 계수의 크기를 줄여주는 방법으로 과대적합을 해결 할 수 있는데, 선형 회귀 모델에서는 릿지와 라소가 활용된다. 릿지는 계수를 제곱한 값을 기준으로 규제를 하고, 라소는 계수의 절댓값을 기준으로 규제를 한다.
# StandardScaler 를 이용해 값을 정규화
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)# 릿지를 이용해 회귀 모델 규제
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)과제
-
ch03(03-1) 2번 문제 출력 그래프 인증하기

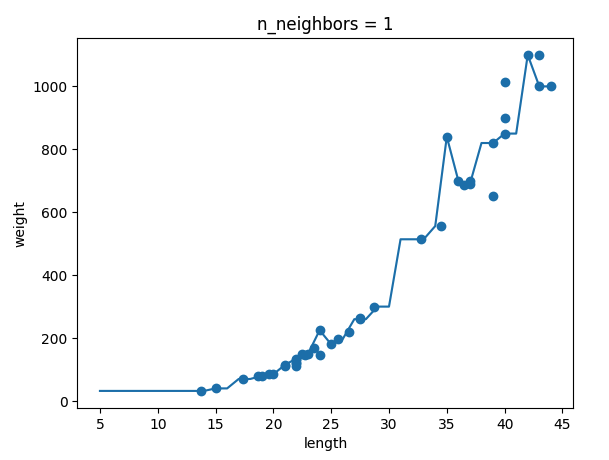
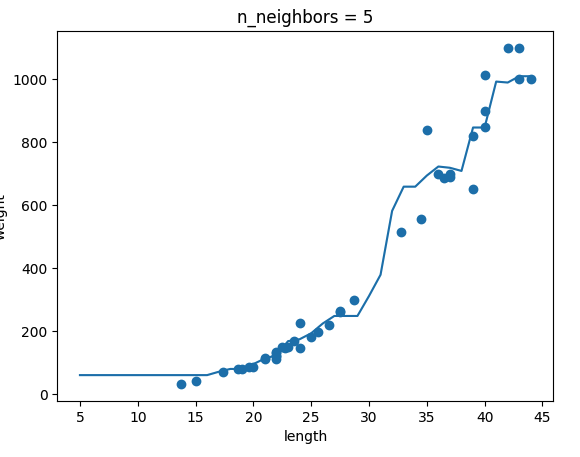
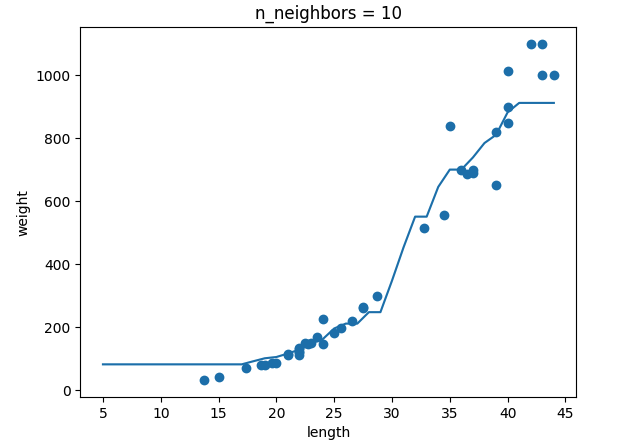
-
모델 파라미터란?
A: 모델이 학습되며 자동으로 조정된 값을 의미합니다. 선형 회귀에서는 최적의 계수와 절편을 찾는데, 이것을 모델 파라미터라고 부릅니다.