로지스틱 회귀
데이터에 대해 확률을 구하기 위해 로지스틱 회귀를 이용해서 z 값을 구한뒤 시그모이드나 소프트맥스 함수를 이용해서 특정 데이터의 결과값의 확률을 예측하는 것이다. 이때 결과값은 수가 아닌 범주형 데이터이다.
이진 분류
결과값의 종류가 2개인 경우 각 행이 1번 범주일지 2번 범주일지만 구하면 되어서 선형 회귀와 매우 비슷하게 나온다. 이 경우 로지스틱 회귀를 이용해 각 행의 z 값을 구해준다. 시그모이드 함수를 이용해서 확률을 구해주는데, z값이 음수이면 확률이 50% 미만으로 나오고 양수이면 50% 이상으로 나온다.
# 로지스틱 회귀(이진분류)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
print(lr.predict_proba(train_bream_smelt[:5]))[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]# z함수 확인
decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)
[-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]# 시그모이드 함수 확인
from scipy.special import expit
print(expit(decisions))[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]다중 회귀
결과값의 종류가 3개 이상인 경우에 해당된다. 로지스틱 회귀 이후에 구한 z 값을 소프트 맥스 함수를 이용해 확률을 구한다. 각 결과 종류마다 확률이 나온다. (ex. 사과, 배, 감이 결과값으로 나올 수 있는 값들이라면 한 행마다 사과, 배, 감일 확률을 각각 구할 수 있다)
# 로지스틱 회귀(다중 분류)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C = 20, max_iter = 1000)
lr.fit(train_scaled, train_target)
proba = lr.predict_proba(test_scaled[:5])[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]# z함수 확인
decisions = lr.decision_function(test_scaled[:5])
print(np.round(decisions, decimals = 3))[[ -6.498 1.032 5.164 -2.729 3.339 0.327 -0.634]
[-10.859 1.927 4.771 -2.398 2.978 7.841 -4.26 ]
[ -4.335 -6.233 3.174 6.487 2.358 2.421 -3.872]
[ -0.683 0.453 2.647 -1.187 3.265 -5.753 1.259]
[ -6.397 -1.993 5.816 -0.11 3.503 -0.112 -0.707]]# 소프트 맥스 함수를 이용해 확률을 구함
from scipy.special import softmax
proba = softmax(decisions, axis = 1)
print(np.round(proba, decimals = 3))[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]확률적 경사 하강법
확률적 경사 하강법은 손실 함수를 점점 줄여나가며 한번에 학습 하는 것이 아닌 점진적으로 모델을 만드는 것이다. 데이터가 많거나 새로운 데이터가 계속 추가 될 때에 사용하는 것이다. 데이터를 여러번 학습 하는데, 이 횟수는 에포크(epoch)라고 한다.
#에포크를 늘렸을때 점수를 구해서 적절한 에포크 찾기
import numpy as np
import matplotlib.pyplot as plt
sc = SGDClassifier(loss = 'log_loss', random_state = 42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes = classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()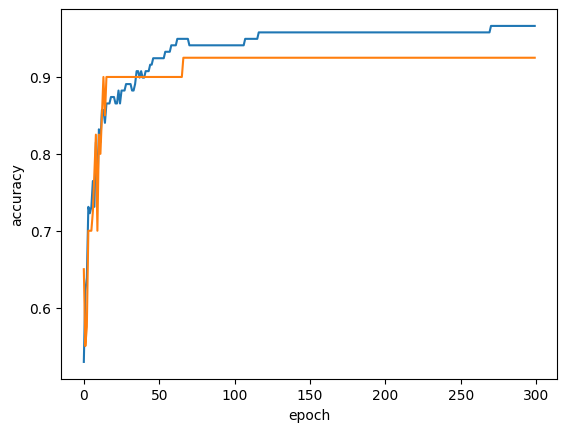
과제
-
로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
A: 시그모이드 함수를 이용해서 -무한대 ~ +무한대인 값을 0과 1 사이의 값으로 바꾸어 주면 해당 값이 확률이다.
-
ch04(04-2) 과대적합/과소적합 손코딩 코랩화면 캡처하기