[MIT 6.006] 10. Depth-First Search ( DFS 탐색 )

Aacara·2023년 5월 14일

자료구조

자료구조 및 알고리즘

목록 보기

10/13

MIT 6.006 Introduction to Algorithms 15강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=IBfWDYSffUU&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=15

지난 강의 배웠던 내용

지난 시간에 배웠던 내용을 키워드로 간단히 정리하면 다음과 같다. 기억이 나지 않는 내용이 있으면 https://velog.io/@aacara/9.-Breadth-First-Search 에서 확인해보자.

그래프 개념 정의
➜ directed/undirected
➜ simple
➜ neighbors
➜ degree
그래프 표현 방법
➜ Adj를 direct access array, Adj(u)를 unsorted array로 표현
path
➜ simple path
➜ path length
➜ distance
➜ shortest path
graph path 문제
➜ Single_Pair_Reachability $(G,s,t)$
➜ Single_Source_Reachability $(G,s)$ DFS⭐
➜ Single_Pair_Shortest_Path $(G,s,t)$
➜ Single_Source_Shortest_Paths $(G,s)$ BFS
Breadth-First Search(BFS)
Single_Source_Shortest_Paths $(G,s)$ 문제를 푸는 알고리즘으로, 실행 시간은 $\textbf{O(|V|+|E|)}$ 이다.

1. Depth-First Search(DFS)

DFS는 Single_Source_Reachability $(G,s)$ 문제를 풀기 위한 알고리즘이다. Single_Source_Reachability $(G,s)$ 는 그래프 G에서 vertice s부터 나머지 vertices까지 가는 path의 존재 유무를 확인하는 문제다. 물론 이 문제를 BFS로 푸는 것도 가능하지만 DFS가 더 적합한 이유를 1-4에서 확인해본다.

1-1. DFS tree

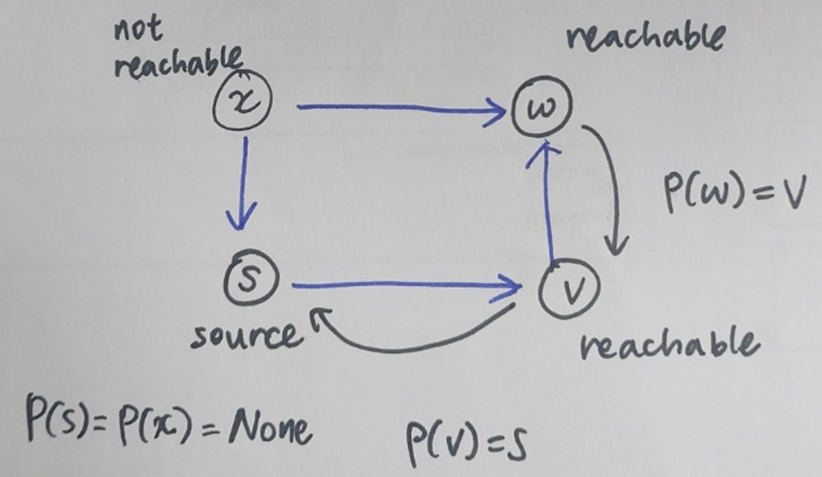
DFS는 BFS처럼 source vertex의 모든 neighbor를 탐색하는 대신에 첫 번째로 탐색한 neighbor 방향으로 최대한 멀리 탐색한다. 탐색의 목적이 BFS는 원천 노드로부터 가장 짧은 경로를 저장하는 것이었지만, DFS는 원천 노드로부터 해당 노드까지 도달하는 것이 가능 여부를 확인하는 것이다. 목적에 따라 경로를 저장하기 위해 BFS와 DFS는 각각 걸맞는 tree를 사용한다. BFS에서 parent vertex $P(v)$ 를 저장함으로써 shortest path tree로 경로를 저장했던 것처럼 DFS도 DFS tree를 통해 탐색 경로를 저장한다. 더 자세히 설명한다면 DFS tree는 $s$ 로부터 탐색의 순서대로 도달한 vertex에 대한 $P(v)$ 를 반환한다.

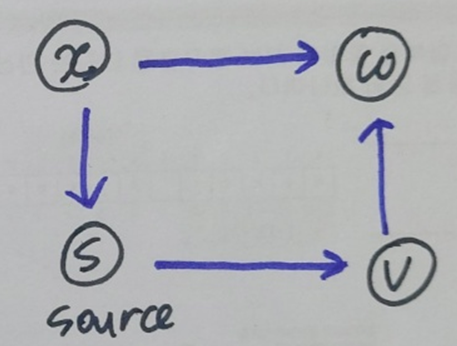
위의 그래프를 G라고 할 때, 각 vertex에서의 parent 노드는 $P(s)$ = s(루트노드), $P(x)$ = None, $P(w)$ = v, $P(v)$ = s이다. Parent node 정보로 DFS path를 구하면 다음과 같다.

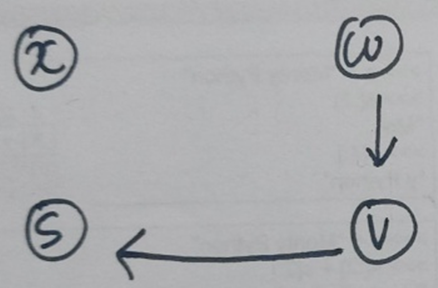
여기까지만 보면 DFS tree와 BFS tree는 차이점이 없어보인다. 하지만, BFS는 최단 경로를 나타내는 반면 DFS tree의 결과는 최단 경로가 아닐 수 있다는 점에서 차이를 보인다.

1-2. 알고리즘

DFS는 BFS처럼 s vertex의 나머지 neighbor를 탐색하기 전에 아직 탐색하지 않은 vertex 중 첫 번째로 탐색한 neighbor 방향으로 최대한 멀리 탐색한다. 그렇게 하기 위해, $Adj^+(u)$ 를 재귀적으로 방문하되, 이미 방문한 vertex는 다시 방문하지 않는다. 만약 탐색 중 모든 $Adj^+(u')$ 가 이미 방문한 vertex라면 $Adj^+(u'')$ 를 기준으로 방문하지 않은 vertex가 있는 지점까지 backtracking, 즉 역추적한다.

위와 같은 그래프에서 원천 노드를 1이라고 할 때, 탐색의 순서는 다음과 같이 두 가지 경우가 있다.

1 > 2 > 3 > 4 > (backtracking) > 5
1 > 2 > 5 > (backtracking) > 3 > 4

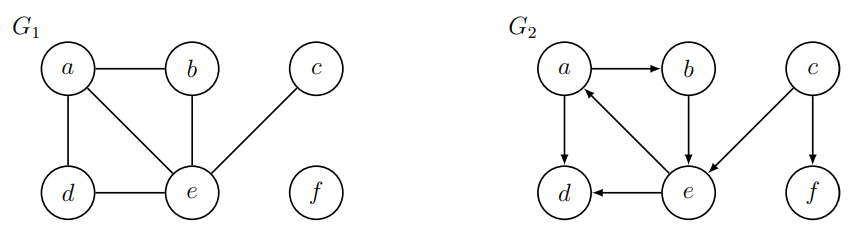
그래프가 directed/undirected 그래프인지에 따라서 single source reachability가 달라지기도 한다. A노드가 원천 노드이고 neighboring vertices 중 알파벳 순서가 낮은 것부터 탐색한다고 가정할 때, $G_1$ , $G_2$ 그래프는 각각 다음과 같은 순서로 탐색이 이루어진다.

$G_1$ : a > b > e > c > d
$G_2$ : a > b > e > d

따라서, $G_1$ 그래프에선, f 노드에 도달할 수 없고, $G_2$ 그래프에선 c와 f 노드에 도달할 수 없다는 것을 알 수 있다.

DFS의 원리 및 탐색 순서에 대해 이해했으니 이제 알고리즘을 코드로 구현해본다. 흐름은 다음과 같다.

P(s) = None으로 설정하고 visit(s)를 실행한다.
visit(u):
- 모든 $v \in Adj^+(u)$ 에 대하여:
  - 만약 P(v) = None이라면:
    - P(v) = u로 설정하고
      visit(v)를 호출한다.

def dfs(Adj, s, parent = None, order = None):
	if parent is None:
    	parent = [None for v in Adj]
        parent[s] = s
        order = []
    for v in Adj[s]:
    	if parent[v] is None:
        	parent[v] = s
            dfs(Adj, v, parent, order)
    order.append(s)
    return parent, order

1-3. 증명

증명은 주장으로부터 시작해서, base case에서 주장이 참임을 밝힌 후, induction에 의해 모든 경우에 대해 확장해서 적용될 수 있음을 밝힌다.

Claim:
1. DFS는 $v \in V$ 인 vertices에 중 도달할 수 있는 곳은 모두 방문한다.
2. $P(v)$ 를 바르게 설정한다.
Base case(k = 0): 원천 노드 s의 P(s)가 바르게 설정되어있으며, s를 방문처리한다.
Induction:
- $\delta(s,v) = k + 1$ 인 vertex v를 상정한다.
  1. s로부터 v까지 가는 경로에서 v 직전의 노드를 u라고 할 때,
    $\delta(u,v) = k$ 이다.
  2. u 노드를 방문처리
  3. $P(u)$ 를 올바르게 설정
- u를 방문하면서 $v \in Adj^+(u)$ 를 고려한다.
  - $P(v) \neq None$ : 이미 방문처리가 된 노드
  - $P(v) = None$ : 아직 방문되지 않은 노드
    이미 방문처리가 된 노드는 방문이 되었고, 아직 방문처리가 되지 않은 노드 v는 u를 방문할 때 방문처리가 된다.
  1. v 노드를 방문처리
  2. $P(v)=u$ 로 올바르게 추가

1-4. 실행 시간

BFS: $\textbf{O(|V|+|E|)}$
BFS의 경우 adjacency list를 훑는데에 소요되는 시간이 $O(|E|)$ , vertices를 초기화하는 데에 걸리는 시간이 $O(|V|)$ 으로 탐색하는 데에 걸리는 총 시간이 $O(|V|+|E|)$ 이다. 따라서, 실행 시간이 입력의 크기와 비례한다는 것을 알 수 있다.
DFS: $\textbf{O(|E|)}$
DFS는 현재 탐색중인 vertex를 v라고 할 때, $P(v)$ 가 없을 때 재귀를 진행한다. 따라서, DFS는 모든 vertex를 한 번 이상 방문하지 않는다. 여기서, DFS는 BFS와 다르게 vertices를 초기화하는 $O(|V|)$ 시간이 걸리지 않는다는 것을 확인할 수 있다. 따라서 vertex v에서의 재귀적인 탐색은 $Adj^+(v)$ 와 비례한다는 것을 알 수 있다. 따라서, DFS의 총 소요 시간이 $O(\sum_{v \in V}deg(v)) = O(|E|)$ 라고 강의에서 결론을 내렸다.

여기서 중요한 점은 DFS가 방문했던 vertex를 방문하지 않는다는 중요한 특성이 있다는 것이다. 방문했던 vertex에 대한 방문을 허용한다면 무한재귀에 빠질 수 있기 때문이다. 그렇기 때문에 $Adj^+(u)$ 중 방문한 노드가 v라고 할 때, $P(v)=u$ 로 저장한다. 이러한 parent 배열의 길이가 $|V|$ 이기 때문에 결국 DFS도 $O(|V|+|E|)$ 시간이 걸릴 것으로 예상된다. 하지만, 모든 vertex를 방문할 필요 없고 지나가는 edge의 개수와 vertex의 개수가 비례하므로 $O(|E|)$ 시간이 걸린다고 교수님이 설명해준 것 같다. 하지만, 2.fullDFS에선 하나의 vertex로부터 접근 가능한 vertices를 구하는 것이 아닌 모든 vertices를 방문해야하므로 $O(|V|+|E|)$ 이 걸린다. 매우 헷갈리는 부분이어서 한참을 고민했다. (! 이 부분 흐름은 저의 개인적인 생각입니다.)

결론적으로, Single_Source_Reachability $(\textbf{G, s)}$ 문제에 BFS는 $\textbf{O(|V|+|E|)}$ , DFS는 $\textbf{O(|E|)}$ 시간이 걸린다. 따라서 reachability 문제에 BFS보다 DFS를 선호한다.

또한 실행시간 뿐만 아니라 공간 복잡도 측면에서도 DFS가 우위에 있다. 만약 최대 깊이를 H라고 한다면, BFS의 공간 복잡도는 $O(|V|)$ 이다. 다음 깊이의 노드를 모두 생성하기 위해 현재 깊이의 노드를 모두 저장해야하기 때문이다. 그에 반해 DFS의 공간 복잡도는 $O(|H|)$ 인데, 그 이유는 시작 노드부터 현재 경로까지의 노드와 미탐색 노드에 대한 정보만 저장되기 때문이다.

또한 DFS가 만약에 운이 좋게?(확률에 의해 좌우되겠지만) 한번 만에 경로를 찾을 수 있다면 이 때 불필요한 나머지 경로들을 저장하는 BFS에 비해 훨씬 효율적이다. 빅오 표기법은 최악일 경우의 실행 시간을 나타내는데, 최선의 경우에는 DFS가 확실히 BFS에 비해 경쟁력이 있을 것이다. 따라서, 최악의 경우에서나 최선의 경우에서나 reachability 문제에 DFS를 쓰는 것이 좋다.

2. Full-BFS & Full-DFS

여태 Single_Source_Reachability $(G,s)$ 문제를 다루었다. 하나의 원천 노드로부터 그래프의 모든 vertex에 도달할 수 없는 경우가 당연히 생긴다. 그렇기 때문에 전체 그래프를 탐색으로 문제의 범위를 넓혀본다.

핵심 아이디어는 모든 노드를 방문할 때까지 방문하지 않은 노드에 대하여 Single_Source_Reachability $(G,s)$ 혹은 Single_Source_Shortest_Paths $(G,s)$ 문제를 반복한다는 것이다. 이러한 문제를 Full-A라고 하며, Single_Source_Reachability $(G,s)$ 를 반복하면 Full-DFS, Single_Source_Shortest_Paths $(G,s)$ 를 반복하면 Full-BFS이다. Full-DFS를 코드로 구현하면 다음과 같다.

for $v \in V$
- if v in unvisited
  - DFS(v)

def full_dfs(Adj):
	parent = [None for v in Adj]
    order = []
    for v in range(len(Adj)):
    	if parent[v] is None:
        # 자기 자신을 parent로 정함, 즉 루트로 지정
        parent[v] = v
        dfs(Adj, v, parent, order)
    return parent, order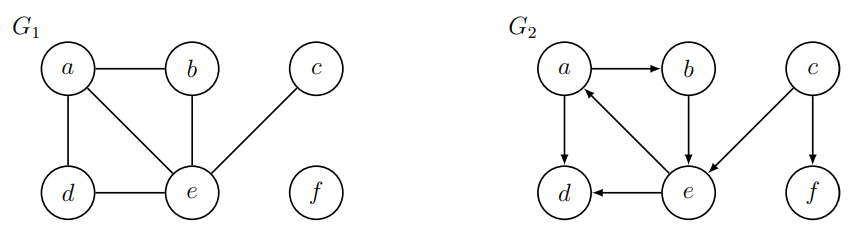

Directed/undirected 그래프에서 전체 그래프 탐색 문제를 Full-BFS, Full-DFS로 각각 풀어본다. 알파벳 순으로 탐색한다고 가정한다.

$G_1$ 그래프
- Full-BFS:
  a (source node 1) > b > d > e > c
  f (source node 2)
- Full-DFS:
  a (source node 1) > b > e > c > d
  f (source node 2)
$G_2$ 그래프
- Full-BFS:
  a (source node 1) > b > d > e
  c (source node 2) > f
- Full-DFS:
  a (source node 1) > b > e > d
  c (source node 2) > f

Full-DFS와 Full-BFS의 실행 시간은 $\textbf{O(|V|+|E|)}$ 으로 같다. 따라서, 전체 그래프를 탐색하는 경우 BFS, DFS 중 어떤 것을 선택하더라도 괜찮지만, topological sorting과 관련되어서 Full-DFS를 더 자주 선택한다. 이는 4. Topological sort에서 확인해본다.

3. Graph Connectivity

앞서, 그래프의 경로와 관련된 5개 문제를 해결하였다.

➜ Single_Pair_Reachability $(G,s,t)$
➜ Single_Source_Reachability $(G,s)$
➜ Single_Pair_Shortest_Path $(G,s,t)$
➜ Single_Source_Shortest_Paths $(G,s)$
➜ Full-A

이제 그래프가 연결되어 있는지 확인하는 새로운 문제를 해결해본다.

➜ Connectivity $(G)$
➜ Connected_Components $(G)$ : $G = (V, E)$ 가 주어졌을 때, $V$ 를 $V$ 의 부분집합 $V_i \subseteq V$ 으로 나눈다. 각 $V_i$ 는 연결되어 있고, $i \neq j$ 인 $V_i, V_j$ 를 연결시키는 edge는 존재하지 않는다.

Graph connectivity 문제는 undirected 그래프에 한정시켜서 생각한다. Directed 그래프의 경우 연결 여부를 생각하기에 복잡하기 때문이다.

문제를 해결하는 방법은 Full-A를 한 번 수행할 때마다 방문한 노드를 연결된 구성 요소에 추가한다. 즉, Full-DFS나 Full-BFS를 통해 그래프의 연결성 문제도 해결할 수 있다.

4. Topological Sort

4-1. DAG

DAG(directed acyclic graph)는 directed graph로 directed cycle을 포함하지 않는다. 다시 말해서, 원천 노드로 돌아오는 경로가 존재하지 않는다. DAG의 예로 트리 그래프가 존재한다.

4-2. Topological Order

그래프 $G(V,E)$ 에 대한 Topological Order란 $(u,v) \in E$ 인 모든 edge에 대하여 $f(u) < f(v)$ 를 만족하는 순서 f이다.

Finishing Order란 Full-DFS가 그래프 G에 있는 각 vertex를 방문하는 것을 마치는 순서로, finishing order를 역순으로 나열하면 topological order이다.

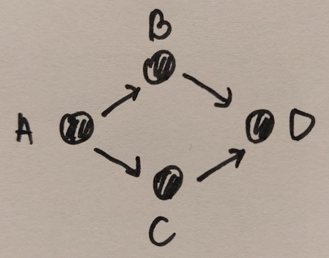
강의에서 Justin Solomon 교수는 위의 DAG그래프를 topological order로 나열하면 두 가지 경우가 가능하다고 하였다. 여기서 topological order는 유일하지 않다는 것을 알 수 있다.

A > C > B > D
A > B > C > D

4-3. 증명

Claim: 그래프 $G(V, E)$ 가 DAG라면,
topological order는 finishing order의 역순이다.

Proof: $(u, v) \in E$ 인 모든 edge에 대하여,
u가 v 전에 ordered되면,
v에 대한 방문이 u 전에 완료된다.
1. u를 v 전에 방문

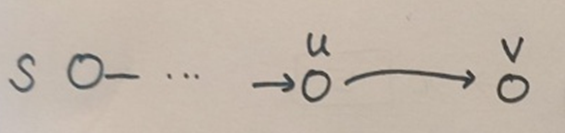
visit(u)가 visit(v)를 호출한다. 따라서, visit(v)가 visit(u) 전에 완료된다.
2. v를 u 전에 방문

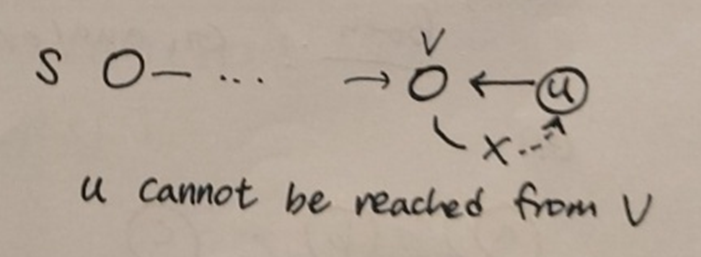
visit(v)가 visit(u)를 호출할 수 없다. 그 이유는 그래프가 acyclic하기 때문이다. 따라서, visit(v)는 u 노드를 보기 전에 완료된다.

4. Cycle Detection

Full-DFS는 그래프 $G(V, E)$ 가 acyclic하다면 topological order를 찾을 것이다. 이 말은 , full-DFS의 finishing order의 역이 topological order가 아니라면 그래프 G가 cycle을 포함한다는 말과 동치다.

먼저, 그래프 G가 acyclic한지 확인하려면, 각 edge (u, v)에 대하여 finishing order에 v가 u전에 있는지 확인한다. Hash table이나 direct access array를 사용한다면 이 작업의 실행 시간은 $O(|E|)$ 이다.

그래프에서 cycle이 존재할 때, cycle을 반환하기 위해서는 Full-DFS에서 노드 s로 돌아가는 ancestor의 set을 유지시켜야 한다.

Claim: 그래프 G가 cycle을 포함한다면, Full-DFS가 v로부터 v의 ancestor에 속하는 edge를 지나갈 것이다.

Proof: G 그래프에서의 cycle $(v_0, v_1, ..., v_k, v_0)$ 이 있다고 가정하자.
- W.L.O.G(without loss of generality), $v_0$ 를 DFS가 가장 먼저 방문한 노드라고 한다.
- 각 $v_i$ 에 대하여 $v_i$ 가 finish되기 전에 $v_{i+1}$ 을 방문하고 finish한다.
- $(v_i, v_{i+1})$ 에 대하여 $v_{i+1}$ 을 아직 방문하지 않았다면, 바로 방문한다.
- 따라서, $v_0$ 에 대해 finish하기 전, $v_k$ 를 방문할 것이다.
- 그렇기 때문에, $v_k$ 에 대해 finish하기 전, $(v_k, v_0)$ 을 고려한다. 여기서, $v_0$ 는 $v_k$ 의 조상이다.
  - $(v_k, v_0)$ 가 존재한다면 그래프 G는 cycle을 포함
  - $(v_k, v_0)$ 가 존재하지 않는다면, 그래프 G는 acyclic