MIT 6.006 Introduction to Algorithms 16강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=5cF5Bgv59Sc&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=16

여태 배운 내용

지금까지 9. 10강에 거쳐 다양한 그래프 문제를 풀었다.

• graph path 문제
  ➜ Single-Source Shortest Paths BFS $\textbf{O(|V|+|E|)}$
  ➜ Single-Source Reachability DFS $\textbf{O(|E|)}$
  ➜ Connected Components BFS, DFS $\textbf{O(|V|+|E|)}$
  ➜ Topological Sort in a DAG full DFS $\textbf{O(|V|+|E|)}$

1. Weighted Graphs

1-1. 정의

여태 배운 distance는 path에 있는 edges의 수였다. 이때 다뤘던 그래프는 모든 edge의 가중치가 같은 특수한 경우였다. 이제 그래프의 범위를 넓혀 각 edge와 연관된 정수가 서로 다를 수 있는 경우를 살펴본다. 이러한 그래프를 weighted graph라고 하며 보다 더 정확한 정의는 다음과 같다.

weighted graph
$w:E \rightarrow Z$를 가지는 그래프 $G = (V,E)$

• 각 edge $e = (w,v) \in E$가 정수 weight $w(e) = w(u,v)$를 가지고 있음

이때의 distance는 path에 있는 edge와 연관된 정수들의 합이다.

1-2. 저장 방식

Weighted graph를 저장하기 위해 기존의 그래프에 edge를 추가적으로 고려해야 한다. Weight를 나타내기 위해 두 가지 방법이 있다. 첫 번째 방법은 기존의 그래프 표현에 edge weight를 adjacency list에 있는 vertex와 함께 저장하는 것이다. 또는 기존의 그래프와 별도로 각 edge와 weight를 매핑해주는 set 자료구조를 저장해도 된다. 여기서는 vertex와 함께 weight를 저정하는 방법을 예시로 들어보자. 다음과 같이 directed 그래프인 $W1$과 undirected 그래프 $W2$를 저장해본다.


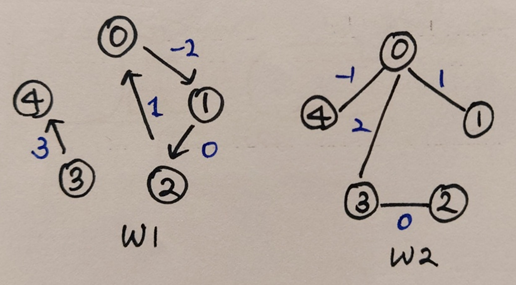
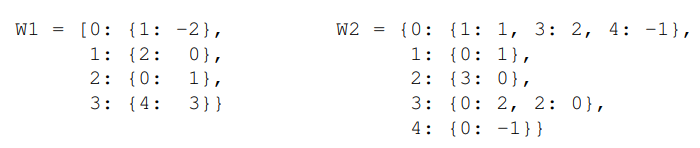
그래프 $W1$과 $W2$의 Adj를 hash table, Adj(u)를 각 vertex로부터 weight를 매핑하는 hash table으로 표현하였다. 이렇게 표현한 이유는 hash table을 쓴다면 $O(1)$ 시간 내에 에지의 가중치를 쿼리할 수 있기 때문이다. 추가적으로 이 방법은 $O(|E|)$ 공간을 사용한다.

2. Weighted Shortest Paths

2-1. Weighted Paths

Weighted path는 weighted graph에서의 경로이며 weight of the path는 경로 상에 있는 edge의 weight의 합이다.

weighted path
$\pi = (v_1, ..., v_k)$

weight of the path
$w(\pi)= \displaystyle\sum_{i=1}^{k-1}w(v_i, v_{i+1})$

2-2. Weighted Shortest Paths Algorithms

2-2.1 Single-source Shortest Paths 문제

Weighted graph와 weighted shortest path 용어를 정리한 이유는 Single-Source Shortest Paths 문제를 weighted graph에 대해 풀기 위함이다. 이 문제는 source 노드로부터 그래프의 모든 vertex v에 대한 최소 가중치 경로를 구하는 문제로 최소 가중치 경로가 없음을 나타낼 수도 있다.

(weighted) shortest path
$s \in V$로부터 $t \in V$까지 가는 경로 중 최소 가중치를 갖는 경로

• $\delta(s,t) = inf\{w(\pi)|\ path\ \pi\ from\ s\ to\ t\}$
  만약 $s$로부터 $t$로 가는 경로가 없다면, $\delta(s,t) = \infin$

앞서 Single-Source Shortest Paths 문제를 BFS를 통해 풀었었다. 다만, 이 때 그래프는 unweighted 그래프라는 제약 조건이 있었다. Unweighted 그래프는 모든 edge의 weight가 1인 그래프를 의미하는데, 만약 모든 weight가 양수이며 서로 같다면 모든 weight 값이 1이 되도록 나눠서 BFS를 통해 최단 경로를 찾은 후 나눴던 값으로 다시 곱하면 된다. 더 나아가 weight가 양수이며 서로 같지 않더라도 edge의 weight 정수 크기만큼 weight가 1인 edge 여러 개로 나누면 된다. 이 때 주의할 점은 weight가 vertices와 edges의 수보다 너무 크다면, $O(|V|+|E|)$ 시간에 BFS로 풀 수 없을 것이다. 결론적으로 weight가 양수이고 bounded되어 있다면 Weighted 그래프에 대하여 SSSP 문제를 BFS로 $O(|V|+|E|)$ 시간에 풀 수 있다.

2-2.2 Negative-Weight Cycles

BFS로 SSSP를 풀 때 weight가 양수인 경우에 대해서만 풀 수 있는 이유가 negative-weight cycles에 있다. Cycle을 돌 수록 $w(\pi)$에 음수가 더해져 음의 무한대로 수렴해 최솟값을 구할 수 없기 때문이다. 정의는 다음과 같다.

negative-weight cycles
동일한 vertex에서 시작하고 끝나는 $w(\pi) < 0$인 경로

따라서, 만약 negative-weight cycle을 거치는 s로부터 v까지의 경로가 존재한다면 $\delta(s,v) = -\infin$이다.

추가적으로 덧붙이자면, $\delta(s,t) = inf\{w(\pi)|\ path\ \pi\ from\ s\ to\ t\}$ 표현에서 minimum min이 아닌 infimum inf은 negative-weight cycle이 존재할 수 있다는 점을 고려한 표현이다. Negative-weight cycle이 존재할 땐 최단 경로가 아닌 사이클 자체를 구하는 것도 방법이다.

2-2.3 Shortest Paths를 구하는 다양한 알고리즘

Shortest-path weights를 구하기 위해 여러 9,11,12,13강에 걸쳐 다양한 알고리즘을 배운다. 각 알고리즘은 그래프의 형태나 weight에 대해 제약 사항들이 있다.

9강 Breadth-First Search라는 첫 번째 알고리즘을 이미 배웠다. 실행 시간은 $O(|V|+|E|)$이지만 unweighted 그래프에 한하는 제약 조건이 있었다. 이번 시간에는 일반적인 weighted 그래프에 대해 SSSP 문제를 O(|V|+|E|) 시간에 푸는 DAG Relaxation 알고리즘에 대해 배운다. 이 때 그래프는 DAG라는 특수한 그래프인데 자세한 설명은 https://velog.io/@aacara/10.-Depth-First-Search#4-1-dag 에서 확인할 수 있다.

2-3. Shortest-Paths Tree

BFS에선, 탐색하는 동안 부모 포인터를 추적하였다. 하지만 DAG relaxation에선 weighted shortest path distance를 먼저 구하고 필요하다면 distance로부터 가장 짧은 경로 상의 부모 포인터를 구하는 접근 방식을 취한다. 여기서 주의할 점은 필요한 부모 포인터가 $\delta(s,v)$가 유한한 값인 vertex v에 대한 포인터라는 점이다.

DAG relaxation의 $O(|V|+|E|)$ 실행 시간이 유효하기 위해선, $v \in V$인 vertices의 $\delta(s,v)$를 알았을 때, shortest-path tree를 $O(|V|+|E|)$ 시간에 구할 수 있어야 한다.

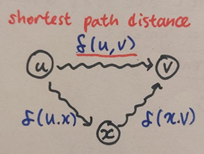
Shortest-path tree를 구하는 방법은 다음과 같다. 참고로 u vertex는 다음 그림과 같이 최단 경로 상 v vertex 직전에 오는 노드다.

---

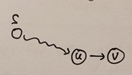
Initialize empty $P$ and $P(s)=None$

• For each vertex $u \in V$ where $\delta(s,u)$ is finite:
  • For each $v \in Adj^+(u):$
    • if v not in P and $\delta(s,v) = \delta(s,u) + w(u,v)$,
      set $P(v)=u$

---

모든 vertices와 outgoing adjacencies를 한 번만 탐색하므로 distance로부터 $P(v)$를 구하는 실행 시간이 $O(|V|+|E|)$이다. Distance로부터 $P(v)$를 구하는 방법과 실행 시간을 확인하였으니 앞으로 나오는 내용은 distance 자체를 구하는 데에 초점을 둔다.

3. Relaxation

3-1. 일반적인 Relaxation

DAG Relaxation 알고리즘을 배우기 전, relaxation 알고리즘이 최적화 문제에 대한 솔루션을 찾는 방법을 알아보자. Relaxation 알고리즘은 최적이 아닌 솔루션으로 시작하여 최적화 문제에 대한 최종 솔루션을 찾을 때까지 반복적으로 솔루션을 개선한다.

그렇다면 relaxation을 이용해서 SSSP 문제를 풀어보자. SSSP 문제는 그래프의 소스 노드에서 각 vertex까지의 최단 경로의 가중치 $\delta(s,v)$를 찾고자 한다. 이때 최적이 아닌 솔루션으로 시작하는 방법은 $s$로부터 $v$까지 가는 최단 경로에 대한 상한선을 $d(s,v)=\infin$으로 설정한다. 물론 simple graph를 상정하므로 $d(s,s) = 0$이다. 그런 다음 추정된 $d(s,v)$가 $\delta(s,v)$가 될 때까지 relax한다. 모든 최단 경로의 추정치가 완전히 완화되면 문제가 해결된다.

def general_relax(Adj, w, s):
	d = [float('inf') for _ in Adj]
    parent = [None for _ in Adj]
    while True:
    	relax some d[v] ??
    return d, parent

Relaxation 알고리즘의 전체적인 흐름을 알아보았으니 이제 vertices를 relax하는 방법과 알고리즘의 종료를 어떻게 보장해야하는지를 살펴보자.

Relax하는 방법은 triangle inequality를 사용한다. Triangle inequality에 의하면 u에서 v까지의 최단 경로 가중치가 다른 vertex x를 통과한 u에서 v까지의 최단 경로보다 클 수 없다.

triangle inequality
$\delta(u,v) \leq \delta(u,x) + \delta(x,v)$

• 

Triangle inequality가 깨졌을 때, 즉 $d(s,u) + w(u,v) < d(s,v)$일 때, $d(s,v) = d(s,u) + w(u,v)$로 설정, 즉 relax한다.

def try_to_relax(Adj, w, d, parent, u, v):
	if d[v] > d[u] + w(u,v):
    	d[v] = d[u] + w(u,v)
        parent[v] = u

이제 알고리즘의 종료를 어떻게 보장하는지 알아보자. 그러기 위해선 우선 모든 최단 경로의 추정치가 완전히 완화되면 그 추정치가 실제 최단 경로라는 것을 증명할 수 있어야 한다.

---

termination lemma

• 어떠한 edge도 relax될 수 없다면 모든 $v \in V$에 대해, $d(s,v) \leq \delta(s,v)$이다.

pf) 그에 반하는 $\delta(s,v) < d(s,v)$가 참이라고 한다면 $s$로부터 $v$까지 가는 더 짧은 경로 $\pi$가 있다는 뜻이다. Edge $(a,b)$를 $\pi$에서 $\delta(s,b) < d(s,b)$가 되는 첫 번째 edge라고 가정한다면, edge $(a,b)$는 relax될 수 있으므로 어떠한 edge도 relax될 수 없다면 조건에 반하기 때문에 거짓이다.

---

while some_edge_relaxable(Adj, w, d):
	(u,v) = get_relaxable_edge(Adj, w, d)
    try_to_relax(Adj, w, d, parent, u, v)

여기서 주의할 점은, 만약에 s에서 도달 가능한 곳에 negative weight cycle이 존재한다면, 알고리즘이 종료되지 않는다는 점이다. 사이클을 돌 수록 relax를 무한대로 반복하기 때문이다.

3-2. DAG Relaxation

Negative weight cycle이 존재하지 않는 DAG를 사용한다면 relaxation은 반드시 끝나게 된다. Topological sort order에 따른 모든 vertex에서 나가는 Adj vertices를 한번씩 relax하면 가장 짧은 경로를 구할 수 있다. 이러한 방법을 DAG relaxation이라고 한다.

def DAG_Relaxation(Adj, w, s):
	_, order = dfs(Adj,s)
    order.reverse()
    d = [float('inf') for _ in Adj]
    parent = [None for _ in Adj]
    d[s], parent[s] = 0, s
    for u in order:
    	for v in Adj[u]:
        	try_to_relax(Adj, w, d, parent, u, v)
    return d, parent

3-3. Correctness

여태 그래왔듯이 induction으로 증명해본다.

---

• 모든 vertex v에 대해 DAG relaxation은 $d(s,v) = min{d(s,v)+w(u,v)|u \in Adj^-(v)}$으로 설정한다.
• 따라서 vertex v로 가기 위한 가장 짧은 경로는 반드시 u를 지난다.
• 그렇기 때문에 만약 모든 $u \in Adj^-(v)$에 대해서 $d(s,u) = \delta(s,u)$가 성립한다면, induction으로 인해 $d(s,v) = \delta(s,v)$다.

---

4. 실행 시간

DAG relaxation의 실행 시간을 구해보자. 각 과정에 걸리는 실행 시간을 구하면 다음과 같다.

• 초기화: $O(|V|)$
• Topological sort: $O(|V|+|E|)$
• DFS: $O(1) \times \sum_{u \in V}deg^+(u)=O(|E|)$
• relaxation은 하나의 edge에 대해 한번만 수행하기 때문에 $O(|E|)$

따라서, 총 실행 시간은 $\textbf{O(|V|+|E|)}$이다.

요약하면, 그래프가 DAG일 때, weight에 제약 없이 SSP를 $\textbf{O(|V|+|E|)}$ 시간에 풀 수 있다.