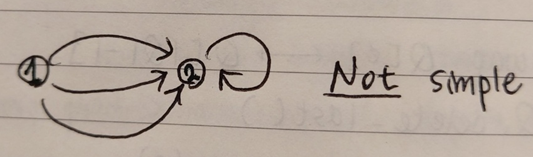MIT 6.006 Introduction to Algorithms 13강을 보고 정리한 내용입니다.
링크: https://www.youtube.com/watch?v=oFVYVzlvk9c&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=13
흐름 정리
1강부터 8강까지 여태 자료구조와 정렬에 대해 다뤘다. Set 또는 sequence Interface와 해당 interface의 연산들을 효율적으로 처리하는 data structure를 배웠고 그 자료구조들로 sorting 알고리즘을 구현해보았다.
9강부터 14강은 그래프 알고리즘을 다룬다. 그래프는 현실세계의 많은 것들, 예를 들어 네트워크 시스템, 퍼즐, 루미큐브, 도로 네트워크를 그래프로 표현할 수 있는만큼 매우 중요하다.
Graph
Terminology
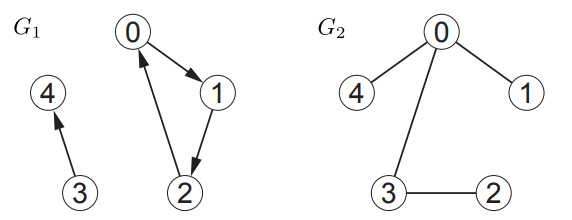
그래프 는 vertices V(노드)의 집합과 vertices의 부분 집합인 두 개의 노드들을 이어주는 edges E의 집합으로 구성된 수학적 객체다. Edges를 로 나타내기도 하는데, edges가 vertices의 쌍이라는 것을 표현하는 식이다. 위의 그래프 과 를 기호로 표현하면 다음과 같다.
위의 과 를 보면 의 원소들은 로 표현한 반면 원소들은 로 표현하였다. 와 가 vertex라고 할 때 는 정렬되어 있는 쌍을 의미하고 이러한 edge들로 구성된 그래프를 directed 그래프라고 한다. 따라서 그래프는 directed 그래프이며 edge를 화살표로 표시한다. 그에 반해, 는 set이기 떄문에 정렬되어 있지 않은 쌍이고 이러한 edge들로 구성된 그래프를 undirected 그래프라고 한다. 같은 맥락으로 그래프는 undirected 그래프이며 edge를 실선으로 표시한다. 참고로 는 순서가 없기 때문에 와 를 모두 의미한다.
Simple Graph
그래프의 범주는 광범위하다. 따라서, 그래프의 범주는 한정시켜 그 안에서 앞으로 생각해보도록 한다. Simple graph라는 그래프를 정의하는데 다음과 같은 특징이 있다.
Simple Graph
- edges are distinct
: 하나의 노드에서 다른 노드로 가는 edge가 하나뿐이라는 뜻으로, 아래 그림에서 1번 노드에서 2번 노드로 가는 길이 3개인 경우에는 simple하지 않다.- edges are pairs of distinct vertices
: 하나의 vertice에서 자기 자신으로 돌아오는 edge가 없다는 뜻으로, 아래 그림과 같이 2번 노드에서 2번 노드로 돌아오는 edge가 있는 그래프는 simple하지 않다.
Simple 그래프라는 조건이 충족되면 비로소 edge와 vertices 사이의 관계를 구할 수 있다. 결론부터 말하자면 이 성립한다. 이에 대한 증명은 다음과 같다.
(i) directed graph
(ii) undirected graph
여기서 잠깐 edges와 vertices 사이의 관계를 구하는 이유를 생각해보자. 그래프 알고리즘을 분석할 때 실행 시간과 차지하는 메모리 공간을 생각해야하기 때문이다. 예를 들어 다음과 같이 생각해볼 수 있다. 보통 많은 그래프들은 sparse하기 때문에 edge의 실행 시간을 구하는 것이 vertices의 제곱의 실행 시간을 구하는 것보다 더 매력적인 선택지일 것이다. 참고로 sparse하다는 것은 가능한 모든 쌍의 조합보다 edge의 수가 적다는 뜻이다.
Neighbor Sets/Adjacencies
그래프에서의 neighbor란 vertices의 쌍에 사이에 edge가 있을 때 해당 vertices를 지칭하는 용어다. Directed graph의 경우 neighbor를outgoing neighbor set와 incoming neighbor set로 구분한다.
outgoing neighbor set
일 때,
예)
incoming neighbor set
일 때,
예)
Incoming/outgoing neighbor set의 크기를 degree라고 한다.
out-degree
일 때,
예)
in-degree
일 때,
예)
앞서 vertices와 edges의 관계를 구했던 것처럼 degree와 edges 사이의 관계를 구하면 다음과 같다.
Undirected graph의 경우 가 곧 이다. 설명을 위해 이 강의에선 , 를 가정한다.
Graph Representations
그래프 개념을 정리하였으니 이제 그래프 를 컴퓨터에 효율적으로 저장하는 방법에 대해 생각해본다. 효율적으로 저장한다는 것은 실행 시간과 메모리 공간 두 가지 요소를 고려한다는 뜻이다. 어떠한 자료구조를 선택하는 것이 좋을지 비교 및 분석할 때 두 가지를 항상 염두해두어야 한다.
우선, 그래프를 저장하기 위해 무엇을 저장해야할지를 생각한다. 가장 먼저 떠오르는 것은 vertex와 vertex 사이에 경로 여부를 0/1로 저장하는 방식이다. 이러한 정보를 저장하기 위한 자료구조는 행렬이다. 하지만 그래프가 sparse한 경우가 많기 때문에 0이 불필요하게 공간을 많이 차지한다.
그렇다면 공간을 효율적으로 사용하기 위해 그래프를 나타내는데에 반드시 필요한 정보만 저장하는 것이 좋겠다. 기본적으로 그래프는 vertex와 edge로 이루어져있다. 따라서, 그래프를 구성하는 모든 vertex에 대하여 vertex u와 해당 vertex에 대해 앞서 정의한 outgoing neighbor edge 정보, 즉 를 저장하면 된다. 이런 방식이라면 그래프를 공간적으로 효율적이게 저장할 수 있다.
그래프를 효율적으로 저장하기 위한 두 가지 요소 중 공간을 충족하였으니 이제 실행 시간을 중심으로 vertices와 outgoing neighbor edge를 저장할 자료구조를 선택한다. 자료구조를 선택하기에 앞서 interface를 정의해야 한다. 그래프를 구성하는 요소들인 vertices는 item 자체에 의미가 있는 intrinsic한 요소이므로 set interface다. 1~8강에서 set interface를 위한 자료구조의 선택지로 unsorted array, sorted array, direct access array, hash table, binary tree가 있다.
그래프를 저장하기 위해 vertex u Adj와 해당 vertex에 매핑되는 Adj(u)를 분리해서 각자에게 적합한 자료구조를 찾아본다.
먼저, Adj의 경우 빠른 실행 시간 안에 vertex를 찾는 자료구조를 선택해야 한다. 따라서, 시간에 key값을 찾는 direct access array나 hash table이 적합하다. 만약 vertices를 로 겹치지 않게 라벨링을 해준다면 key 값이 곧 배열에서의 위치와 같기 때문에 공간을 차지하는 direct access array를 선택한다. 만약 vertices에 대한 라벨링이 되어있지 않다면 hash table을 사용하면 된다.
각 vertice u에 연결되어있는 outgoing edges를 담은 Adj(u)를 adjacency list라고 한다. Adj와 마찬가지로 direct access array나 hash table을 사용할 수도 있겠지만, 우리가 풀 graph path problem에 각 vertex에 연결된 vertex를 시간 안에 찾는 과정이 필요하지 않다. (Graph path problem에 대해서는 Path/ Graph Path 문제에서 더 자세히 설명한다.) 따라서, 보다 단순한 unsorted array만으로도 충분하다.
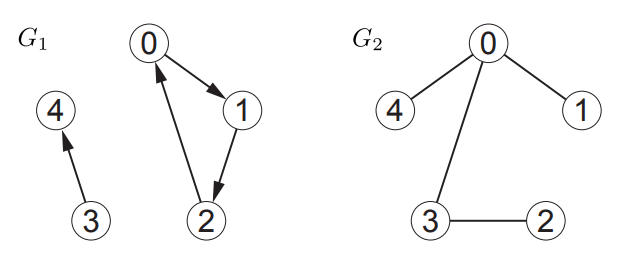
그래프 G1과 G2의 Adj를 direct access array, Adj(u)를 unsorted array로 표현하면 다음과 같다.
| G1 | G2 |
|---|---|
Path
앞서 그래프 의 정의와 저장 방법에 대해 배웠다. 이제는 저장된 그래프를 가지고 경로 문제, 구체적으로는 가장 짧은 경로를 찾는 문제를 생각해볼 것이다. 문제를 풀기 전에 경로가 무엇인지에 대한 정의부터 짚고 넘어간다.
Terminology
Path
Path란 그래프에 존재하는 vertices의 sequence로, sequence에 포함된 인접 vertices 사이에 edge가 있을 때 path라고 한다. Simple 그래프를 가정했던 것처럼 path도 simple한 경우로 한정시켜서 생각해본다.
Simple path
- vertex를 반복하지 않는 path
length
- path에 존재하는 edge 수
- path에 존재하는 vertices의 수 - 1
distance
- 일 때, 부터 까지의 최소 length
- 에서 로 가는 경로가 없을 때,
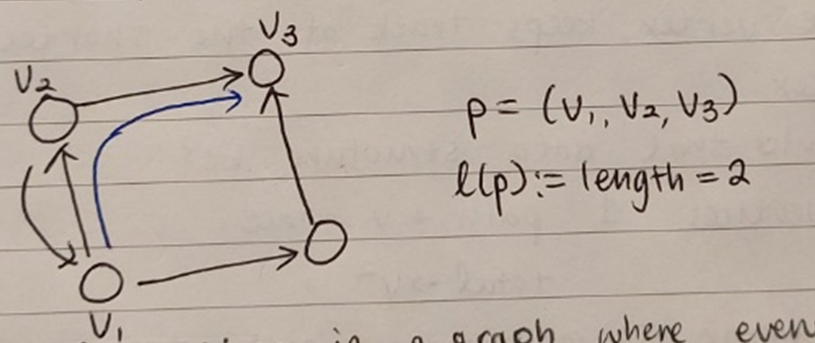
위의 그래프에서 일 때 이고 , 가 된다.
Graph Path 문제
경로 관련 개념과 용어를 정리하였으니 이제 개인적으로 가장 중요하다고 생각하는 문제 정의를 한다. 결국 그래프를 배우는 것도, 경로가 무엇인지 정의내리는 것도 문제를 풀기 위함이다. 그래프 문제는 크게 3가지로 나뉜다.
1. single_pair_reachability(G,s,t)
그래프 G에서 vertice s부터 t까지 가는 path가 존재하는가?
2. single_pair_shortest_path(G,s,t)
Vertice s부터 t까지 가는 가장 짧은 경로와 그 거리, 즉 distance를 반환
3. single_source_shortest_path(G,s)⭐
하나의 source로부터 나머지 모든 vertice로 가는 가장 짧은 경로와 그 거리를 반환
Graph path 3가지 문제를 보면 1번에서 3번으로 갈 수록 문제의 난이도가 높아지는 것을 확인할 수 있다. 모든 문제를 풀 알고리즘을 찾진 않을 거지만, 가장 어려운 single_source_shortest_path(G,s)를 시간에 푸는 것을 목표로 한다.
Shortest Paths Tree
우리가 필요한 자료구조는 하나의 원천 노드로부터 다른 모든 노드로 가는 path를 저장해야 한다. 이렇게 많은 정보를 저장해야 하는 자료구조는 매우 클 것으로 짐작하기 쉽다. 하나의 원천 노드로부터 다른 하나의 노드로 가는 경로는 공간이 필요할 것이고, 만약 원천 노드를 제외한 모든 노드로 가는 경로를 저장하고자 한다면 공간이 필요할 것이기 때문이다.
다행히도 선형적인 공간만 필요로 하는 자료구조가 존재한다. 이러한 자료구조를 사용하기 위해선, 생각의 전환이 필요하다.
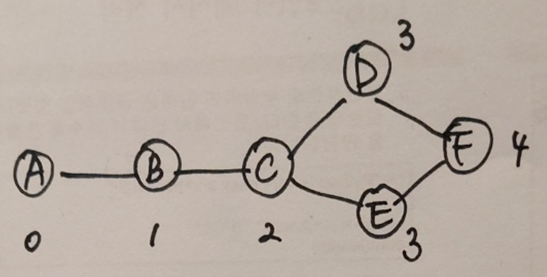
위의 그래프를 살펴보자. A 노드를 원천 vertex라고 할 때, vertice D까지 가는 가장 짧은 path는 이다. 여기서 신기한 점은 가장 짧은 path를 자른 경로 역시 가장 짧은 경로라는 것이다.
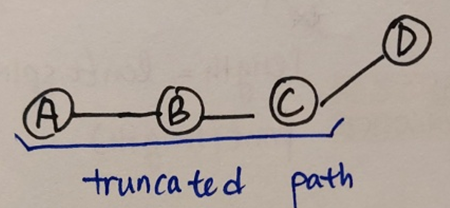
위의 그래프에서 A부터 D까지의 가장 짧은 경로를 자른 경로 역시 A부터 C까지 가는 가장 짧은 경로다. 그렇다면 vertex D 입장에서 자기 자신 전에 오는 하나의 vertex C만 안다면 손쉽게 가장 짧은 경로를 구할 수 있다. 이 개념을 보편화하기 위해 모든 노드에 대해서 가장 짧은 경로 상 직전의 vertex인 를 정의한다.
P(v):
원천 vertex로부터vertex v까지의 최단 경로에서vertex v직전의 vertex
전체 그래프에 대하여 직전 vertex를 가르키도록 그래프를 바꾸면 undirected 그래프가 directed 그래프로 바뀌게 된다. 위의 그래프를 바꾸면, 다음과 같이 변한다.
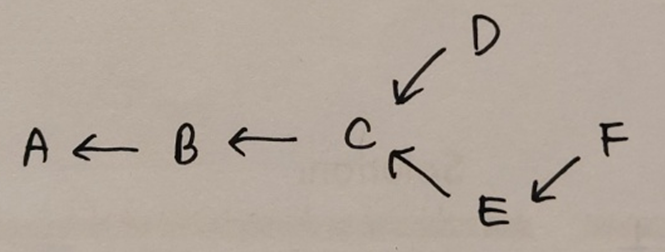
그래프의 vertices들에 순서가 생겼기 때문에 sequence interface에 해당된다. 1~8강에서 sequence interface를 위한 자료구조의 선택지로 array, linked list, binary tree가 있었다. 3개의 선택지 모두 위의 그래프를 저장하는데에 완벽하게 들어맞진 않지만, 그래프에 방향이 있다는 점에서 pointer 개념이 필요하기 때문에 array보단 linked list나 binary tree가 더 비슷하다. 범위를 더 좁혀서 한 노드에서 시작해서 다른 노드를 순회하여 자기 자신에게 돌아오는 순환이 없기 때문에 binary tree 자료구조가 3개의 후보지 중에서 가장 적합해보인다. 하지만, parent node와 left, right child node 형태의 구조가 아니므로 binary는 빼고 tree 구조만 가져오는 것이 우리가 사용하고자 하는 최종 자료구조다. 최단 경로를 저장하는 이러한 자료구조를 shortest path tree라고 한다. Shortest path tree는 의 set을 저장하기 때문에 의 선형적인 공간만을 필요로 한다.
Shortest path tree 구조가 장점만 있는 것은 아니다. 그래프에 edge를 추가한다면, 모든 vertex에 대하여 최단거리의 길이가 바뀐다는 다소 성가신 특징이 있다. 따라서, edge를 추가하거나 삭제할 때마다 새로운 트리를 생성해야 한다.
Breadth-First Search(BFS)
최종적으로 이번 강의에서 풀 문제는 하나의 source 노드로부터 나머지 모든 노드로 가는 가장 짧은 경로와 그 거리를 반환하는 문제다. 이때 연산해야하는 대상은 가장 짧은 거리인 과 더불어 shortest path tree로 저장할 때 필요한 이다.
이제 그래프를 어떻게 탐색해야 할지를 고민해본다. 여기서 그래프 노드를 원천 노드로부터 distance가 증가하는 방향으로 탐색하는 방법을 떠올린다. 원천 노드로부터 distance가 같은 노드들을 묶어줘서 생각하면 편리하게 이러한 탐색을 할 수 있다. 이때 distance가 같은 노드들의 집합을 Level set이라고 한다.
level set
- 원천 노드로부터 거리가 i만큼 떨어져 있는 모든 vertices의 집합
- 모든 vertex 는 과 인접한다.
- 일 때, 에 있는 노드는 에 등장하지 않는다.
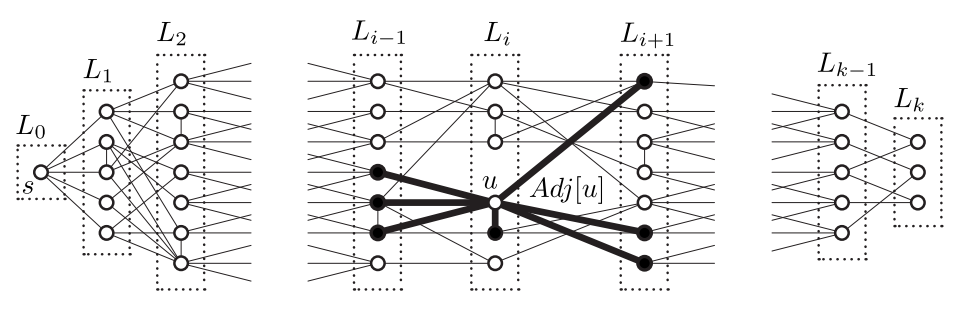
Level set을 통해 path를 찾는 탐색 방법을 Breadth-First Search(BFS)라고 하며, BFS가 저장하는 3가지 개념은 다음과 같다.
BFS
- : 원천 노드 s와 노드 v 사이의 가장 짧은 거리
- : 최단 경로 상에 위치한 노드 v 직전의 노드
- : 같은 최단 경로 거리를 가진 노드들의 집합
BFS를 과정을 증명한 후, 그 과정을 코드로 작성해본다.
-
Base case (i=1): 원천 노드 s로부터 시작한다.
-
Induction: 를 계산한다.
의 모든 vertex 에 대하여
- 이고 일때의 에등장하지 않는모든 에 대하여
1) 를 에 추가
2) 로 설정
3) 로 설정한다.
-
Recursion: 가 공집합이 될 때까지 일때, 를 증가시키면서 로부터 를 계산한다.
-
참고로 가 존재하지 않는다면 로 설정한다.
def bfs(Adj, s):
parent = [None for v in Adj]
parent[s] = s
level = [[s]]
while 0 < len(level[-1]):
level.append([])
for u in level[-2]:
for v in Adj[u]:
if parent[v] is None:
parent[v] = u
level[-1].append(v)
return parent실행 시간
BFS의 총 실행시간은 이다. 메모리에 할당하는 실행시간은 사용하는 메모리 공간의 크기와 비례한다. 따라서, 메모리 공간을 생각해보면 우선, 모든 vertices를 저장한다. 그후 각 vertice의 최단 경로인 edge를 저장한다. 따라서 BFS의 총 실행시간은 그 둘을 더한 이다. 결론적으로 BFS는 선형 실행시간이 걸린다.