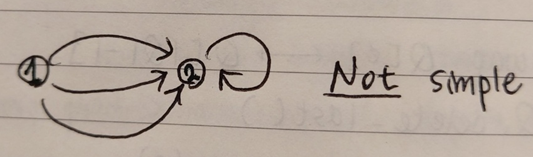
MIT 6.006 Introduction to Algorithms 18강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=f9cVS_URPc0&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=18

여태 배운 내용

Previously

• Shortest-path weights으로부터 shortest-path tree를 $\textbf{O(|V|+|E|)}$ 시간에 풀 수 있음을 증명하였다. 따라서 weights를 구하는 데에 초점을 두고 parent pointer는 우선 신경쓰지 않기로 했다.
• Weighted graphs: 가장 먼저 SSSP(Single Source Shortest Paths) 문제를 unweighted 그래프에 대해 DFS, BFS를 통해 $\textbf{O(|V|+|E|)}$ 시간에 풀었다. 그 후, 그래프를 일반화하여 cycle이 존재하는 weighted 그래프에 대해 SSSP 문제를 풀고자 하였으나, 먼저 cycle이 존재하지 않는 weighted 그래프인 DAG 그래프에 대해 DAG Relaxation을 통해 $\textbf{O(|V|+|E|)}$ 시간에 풀었다.
• DAG 그래프: DAG는 cycle이 없는 그래프로, weight 자체에 대한 제약은 없다. 다시 말해서, weight의 값으로 양수는 물론 0 혹은 음수도 가능하다.

Today

드디어 가장 일반적인 그래프를 다루게 된다. 여기서 말하는 가장 일반적인 그래프는 simple graph 중 cycle이 존재할 수 있으며, weight 값으로 양수, 음수, 0 모두 가능한 그래프를 의미한다.

Simple Graph

• edges are distinct
  : 하나의 노드에서 다른 노드로 가는 edge가 하나뿐이라는 뜻으로, 아래 그림에서 1번 노드에서 2번 노드로 가는 길이 3개인 경우에는 simple하지 않다.
• edges are pairs of distinct vertices
  : 하나의 vertice에서 자기 자신으로 돌아오는 edge가 없다는 뜻으로, 아래 그림과 같이 2번 노드에서 2번 노드로 돌아오는 edge가 있는 그래프는 simple하지 않다.
  

오늘 풀 문제는 SSSP in cyclic graph with negative weights이다. Cyclic 그래프에 음의 가중치가 존재한다면 negative weight cycles가 존재할 수 있다. 그 이유는 원천 노드로부터 reachable할 때 negative weight cycle을 돌 수록 거리가 감소하기 때문이다. 이 말은 즉, 가장 짧은 거리를 구하기 위해 지나가야 하는 edge의 수가 bounded되어 있지 않다는 뜻이기도 하다. 따라서, 해당 거리를 음의 무한대로 설정하고 사이클 자체를 반환한다. 그 외 나머지 reachable한 거리에 대해서는 가장 짧은 유한한 거리를 반환한다. 쉽게 정리하면 다음과 같다.

가정: 모든 vertex에서의 shortest path distance, weights를 구할 수 있다.

• #1. Reachability
  • not reachable: $\infin$
  • reachable through a negative weight cycle: $-\infin$
  • others: 유한한 weight
• #2. negative weight cycle이 있다면, 사이클 자체를 반환

1. 맛보기

1-1. ⭐Directed?⭐ Undirected? 그래프 선택

Q: $Undirected$ graph G가 주어졌을 때, G의 negative-weight cycle 포함 유무를 반환한다.
Undirected 그래프의 경우 negative edge가 존재한다면 왔다갔다 하는 것만으로도 negative weight cycle이 생성된다. 따라서 S를 포함하는 연결 요소가 있으면 negative weight cycle으로부터 접근 가능한 모든 거리가 음의 무한대가 된다. 따라서, 음수의 weight edge가 있다면 $directed$ 그래프에 한정해서 생각한다.

1-2. 실행시간 O(|V|(|V|+|E|)) -> O(|V||E|)

SSSP를 해결하는 알고리즘 A의 실행시간이 $O(|V|(|V|+|E|))$ 걸릴 때, 이를 활용해서 SSSP를 $O(|V||E|)$ 시간에 풀 수 있음을 보여주시오.
직관적으로 생각해보면, $O(|V|(|V|+|E|))$와 $O(|V||E|)$가 다를려면 vertices의 수가 edges의 수보다 압도적으로 많아야 한다. 하지만 simple path는 vertices를 반복 방문할 수 없으므로 원천 노드 S를 포함하는 연결된 요소들의 최대 E+1개의 vertices를 갖고 있다. 따라서, $O(|V|(|V|+|E|)) \approx O(|V||E|)$이다.

이번 강의에서 배울 내용을 미리 단계별로 살펴보면 다음과 같다.

• #1. 우선 그래프가 주어졌을 때 BFS 혹은 DFS를 통해 원천 노드 s로부터 나머지 요소를 신경쓰지 않고 reachable한 vertices만 찾는다면 $\textbf{O(|E|)}$ 시간이 걸린다.
• #2. S로부터 reachable한 vertices들을 확인했으니 reachable하지 않은 vertex들을 $\delta(s,v)=\infin$으로 설정한다. $\textbf{O(|V|)}$
• #3. s로부터 reachable한 vertices로 구성된 그래프 $G' = (V', E')$를 만든다. $\textbf{O(|V|+|E|)}$
• #4. 만들어진 $G'$ 그래프에 A 알고리즘을 수행한다.
  이때, $G'$에서 유한한 거리의 simple path를 구하므로 앞서 설명했듯이$|V'|=O(|E'|)=O(|E|)$이다. $\textbf{O(|V||E|)}$

2. Simple Shortest Paths

• Claim 1: $\delta(s,v)$가 유한하다면, s로부터 v까지 가는 simple한 가장 짧은 경로가 존재한다.

Claim을 증명하기 전, 두 가지 명제를 먼저 염두해두자.

---

• 그래프가 cycle과 negative weight를 포함할 때: Negative-weight cycle을 포함할 수도 있다.
• 그래프가 negative cycle을 포함하지 않을 때: simple하다.

---

• proof: 반대로 cycle이 있는 상황을 가장해본다.

  • simple shortest path가 없다고 가정을 한다. 이때, $\pi$를 vertices가 가장 적은 shortest path라고 한다.

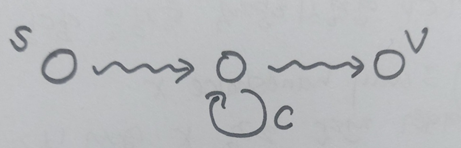
  • $\pi$가 simple하지 않기 때문에 $\pi$에 cycle C가 존재한다. 이때 cycle C의 가중치는 0 혹은 양수이다. Cycle C의 가중치가 음수라면 $\delta(s,v) = -\infin$이 되기 때문이다.
    

  • 만약 cycle C의 가중치가 0 혹은 양수라면, cycle C를 제거할 수 있다. Cycle C가 제거되기 전의 경로를 $\pi$, 제거한 후의 경로를 $\pi'$라고 할 때, $w(\pi') \leq w(\pi)$이다. Cycle을 계속해서 제거하다보면 simple path를 생성할 수 있다.

Claim 1을 요약하면, 그래프에 cycle이 없다면, shortest path는 simple하다. 만약 그래프에 cycle이 있다면, shortest path가 simple하지 않겠지만, $\delta(s,v)$가 유한한 값이라면, shortest path가 simple일 때까지 cycle을 제거할 수 있다.

• Claim 1': Simple paths의 edges 수 $\leq |V|-1$
  Simple path는 vertices를 반복해서 방문하지 않기 때문에 vertices는 최대 $|V|$개 있고, edges는 최대 $|V|-1$개 있다.

Claim 1과 Claim 1'의 흐름을 다시 요약해보면, shortest path는 원래 무한한 갯수의 edges를 가질 수 있다. 하지만 shortest path 거리가 유한하다는 가정 하에는, edges의 개수가 최대 $|V|-1$개이다.

여기서 shortest path 거리 유한 -> edges 수 $|V|-1$에서 화살표의 방향을 바꾸어서 접근해보면 어떨지 상상해보자. 지나갈 수 있는 edges의 수에 상한선을 두고 이를 바탕으로 shortest path 거리를 구하는 것이다. 3. Negative Cycle Witness에서 이러한 접근 방법을 살펴본다.

3. Negative Cycle Witness

지나갈 수 있는 edges의 상한선을 k로 두는 거리를 k-edge distance $\delta_k(s,v)$라고 한다.

k-edge distance $\delta_k(s,v)$
: s로부터 v까지 가는 path 중 $\leq k$ edges를 사용하는 가장 짧은 path

$\delta_k(s,v)$ 개념을 이용해서 다음과 같이 응용해볼 수 있다. $V-1$개의 vertices를 통과하는 가장 짧은 거리 $\delta_{|V|-1}(s,v)$보다 $V$개의 vertices를 통과하는 가장 짧은 거리 $\delta_{|V|}(s,v)$가 더 짧다면, negative cycle이 존재하며 v를 witness라고 한다.

---

• 만약 $\delta(s,v) \ne -\infin$이라면 가장 짧은 거리가 simple하기 때문에 $\delta(s,v) = \delta_{|V|-1}(s,v)$이다.
• $\delta_{|V|}(s,v) < \delta_{|V|-1}(s,v)$ 라면 $\delta_k(s,v) = -\infin$이고 v는 witness

---

Simple path의 최대 edge 수가 $|V|-1$이다. 따라서 이보다 더 많은 갯수의 vertex를 지나가면 거리가 늘어나야 한다. 하지만, 반대로 거리가 준다면, 그래프에서 simple path와 negative cycle이 동시에 존재하는 것이다. Negative cycle이 존재한다는 증명으로 v가 witness가 되는 것이다.

앞서, Claim 1에선 $\delta_k(s,v)$가 유한하다면, s로부터 v까지 가는 simple한 가장 짧은 경로가 존재한다고 했다. 이제 $\delta_k(s,v)$가 음의 무한대인 경우를 살펴보자.

• Claim 2: $\delta_k(s,v) = -\infin$이라면, $v$는 witness로부터 reachable하다.

• proof: s로부터 reachable한 모든 음수의 weight cycle은 witness를 포함한다. 를 증명해본다.

  • 우선 s로부터 reachable한 negative weight cycle C를 고려한다.
    

  • $v, \in C$, $v' \in C$에 대하여 $v'$을 $v$의 predecessor이라고 하자. 이때, $\displaystyle\sum_{v \in C}w(v',v) < 0$으로 가정한다.

  • $\delta_{|V|}(s,v) \leq \delta_{|V|-1}(s,v) + w(v',v)$
    ※ $\delta_{|V|}(s,v)$가 가장 짧은 거리이므로 $\leq$ 등호로 나타냄

  • $\displaystyle\sum_{v \in C}\delta_{|V|}(s,v) \leq \displaystyle\sum_{v \in C}\delta_{|V|-1}(s,v) + \displaystyle\sum_{v \in C}w(v',v)$ --- (1)
    ※ 모든 vertices에 대한 합

  • $\displaystyle\sum_{v \in C}\delta_{|V|-1}(s,v) + \displaystyle\sum_{v \in C}w(v',v) < \displaystyle\sum_{v \in C}\delta_{|V|-1}(s,v)$ --- (2)
    ※ $\displaystyle\sum_{v \in C}w(v',v) < 0$이므로 좌변의 값이 우변의 값보다 작음

  • $\displaystyle\sum_{v \in C}\delta_{|V|}(s,v) < \displaystyle\sum_{v \in C}\delta_{|V|-1}(s,v)$
    ※ (1), (2)번 식 결합

  • $\delta_{|V|}(s,v) < \delta_{|V|-1}(s,v)$ --- (3)
    ※ 하나의 vertex에 대한 식

  • 만약 C에 witness가 없다면, $\delta_{|V|}(s,v) \geq \delta_{|V|-1}(s,v)$ --- (4)

  • (3)과 (4)는 모순이므로 C에 witness가 존재해야 한다.

4. Bellman-Ford

4-1. 변형된 Bellman-Ford

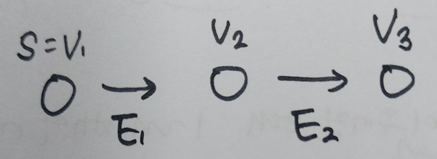
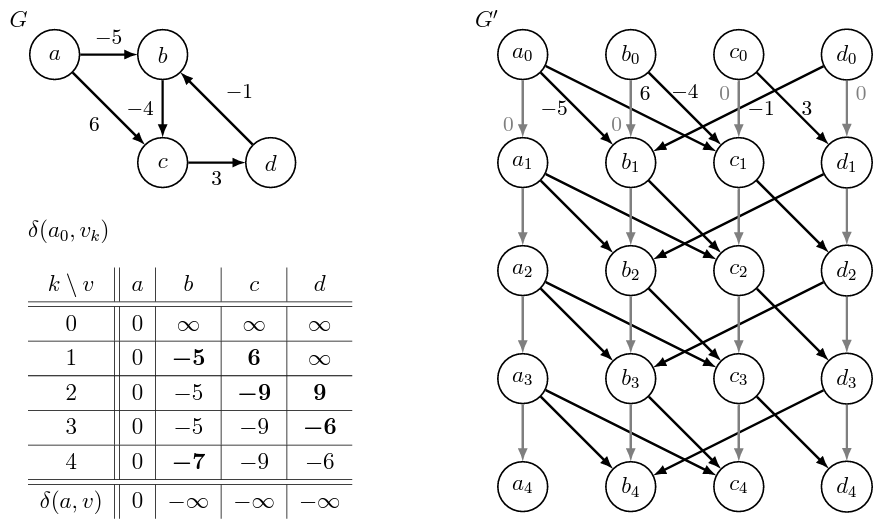
이번 강의에선 더 원활한 분석을 위해 변형된 벨만 포드 알고리즘을 살펴본다. 변형된 벨만 포드 알고리즘은 11. Weighted Shortest Paths 에서 배운 DAG relaxation을 적용하기 위해 그래프를 DAG 그래프를 만든다. 구체적으로, graph duplication을 이용해서 vertex를 복사해 $|V|+1$개의 레벨을 만든다. 여기서 $k$ 레벨에 있는 $v_k$는 s로부터 v까지 $\leq k$ edge를 이용해서 도달한다는 뜻이다. 만약 edge를 더 높은 레벨에만 연결한다면, 새로 만든 이 그래프는 DAG이다. 따라서, 벨만 포드는 그래프를 V배로 복제$O(|V|)$한 후 SSSP 알고리즘을 DAG 그래프에 대해 수행$O(|V|+|E|)$하므로 총 실행시간이 $\textbf{O|V|(|V|+|E|)}$이다.

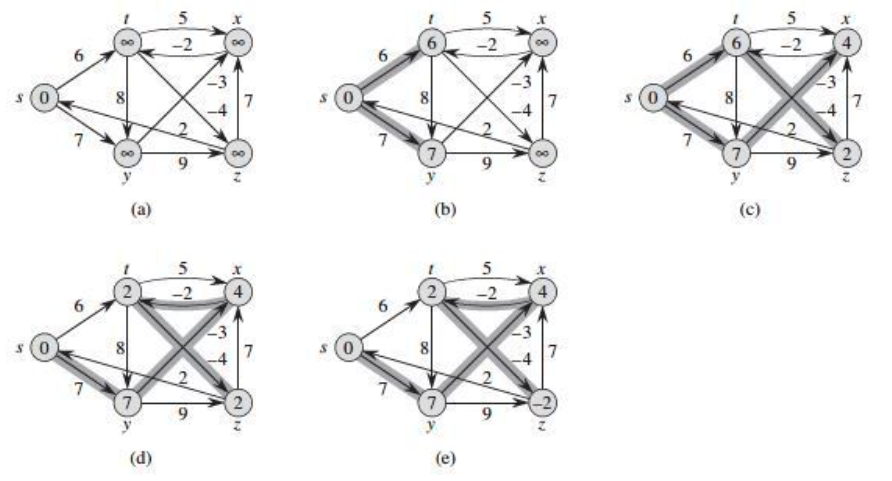
Negative weight cycle을 포함하는 directed 그래프를 예를 들어보면 다음과 같다. $G$ 그래프로부터 $G'$ 그래프를 만들 때, vertices의 수는 $|V|(|V|+1)$이고 edges의 수는 $|V|(|V|+|E|)$이다. Vertices의 경우 V개의 노드를 V번 이동할 수 있도록 원래의 노드에서 추가적으로 복제하기 때문에 $|V|+1$을 곱해주고, edges의 경우, vertex 자기 자신으로 가는 경로 $|V|$개와 edge 수 $|E|$를 더한 수에 $|V|$를 곱한다.

4-1.1. 알고리즘 단계 및 실행시간

Bellman-ford 알고리즘의 과정은 다음과 같다.

---

• #1. $G=(V,E)$ 그래프로부터 DAG 그래프 $G'=(V',E')$을 생성한다. $O|V|(|V|+|E|)$

  • $G'$의 vertices: $|V|(|V|+1)$

    • $v \in V$, $k \in \{0,...,|V|\}$인 모든 $v_k$에 대해 성립

  • $G'$의 edges: $|V|(|V|+|E|)$

• #2. $G'$ 그래프에 대핸 $S_0$를 원천 노드로 하는 SSSP를 DAG relaxation로 수행. 이때 $v_k \in V'$인 모든 $v_k$에 대하여 $\delta(s_0, v_k)$를 계산한다. $O(|V|+|E|)$

  • 2-1) 모든 vertex에 대해 $d(s,v) = \delta(s_0, v_{|V|-1})$로 설정한다. $O(|V|)$
  • 2-2) 모든 witness $u \in V$에 대해 $\delta_{|V|}(s,v) < \delta_{|V|-1}(s,v)$인 경우: $O(|V|)$
    • 그래프 $G$에서 $u$로부터 reachable한 모든 vertex $v$에 대해:
      • $d(s,v) = -\infin$ $O(|E|)$

---

4-1.2. Correctness

• Claim 3: 모든 $v \in V$, $k \in \{0, ..., |V|\}$에 대하여 $\delta(s_0, v_k) = \delta_k(s,v)$
  ※ 거리가 유한한 모든 정점에 대해 최단 경로 거리를 올바르게 설정한다.

• proof: $k$에 대한 induction을 수행한다.

  • Base case: $k=0$일때 모든 $v \in V$에 대하여 참이다.
    예를 들어, $s_0$으로부터 reachable한 원소 $v_0$는 $v=s$, 즉 자기자신이다.

  • Inductive step: $k < k'$에 대해 참이라고 가정한 후, $k=k'$에 대해 증명

    • $\delta(s_0, v_k)$
      $= min\{\delta(s_0, u_{k'-1})+w(u_{k'-1}, v_{k'})|u_{k'-1} \in Adj^-(v_{k'})\}$ --- (1)
      $= min\{\delta(s_0, u_{k'-1})+w(u, v)|u \in Adj^-(v_{k'})\} \cup \{\delta(s_0, v_{k'-1})\}$ -- (2)
      $= min\{\delta_{k'-1}(s, u)+w(u, v)|u \in Adj^-(v)\} \cup \{\delta_{k'-1}(s, v)\}$ -- (3)
      $= \delta_{k'}(s,v)$ -- (4)

    ※ 식 해설
    (1) $v_k$까지의 최단 거리 $\delta(s_0, v_k)$는 $v_{k-1}$까지의 최단 거리 $\delta(s_0, v_{k-1})$에서 하나의 edge의 가중치를 더한 값과 같다.
    (2) $Adj^-(v_k')$에 속하는 $u_{k'-1}$ 대신 $Adj^-(v)$에 속하는 모든 정점 $u$ 순회한다. 즉, 더 일반화하였다. 뒤에 합집합이 붙은 이유는 $v$ vertex까지 가는데에 최대 k개의 edge를 통과할 수 있는데 k-1개의 edge만 통과했을 때 거리가 더 짧을 가능성이 있기 때문이다.
    (3) $k < k'$에 대해 참이라고 가정했기 때문에 $\delta(s_0, u_{k'-1}) = \delta_{k'-1}(s, u)$이다.
    (4) 정의에 의해 (3)식은 최대 $k'$ edges를 통과하는 최단거리를 구했다.
    

• Claim 4: 벨만 포드 알고리즘을 수행하면 $d(s,v) = \delta(s,v)$, 즉 하나의 원천 노드로부터 모든 vertices의 거리가 최단거리이다.

• proof: 모든 $v\in V$인 $\delta_{|V|-1}(s,v)$에 대해 Claim 3에 의해 구한다.

  • $\delta(s,v) \ne -\infin$일때, $d(s,v) = \delta_{|V|-1}(s,v) = \delta(s,v)$
  • $\delta(s,v) = -\infin$일 때, Claim 2에 의해 witness로부터 reachable한 모든 vertex $v$에 대해 $d(s,v) = -\infin$으로 설정한다.

4-2. 오리지널 Bellman-Ford

4-2.1 변형된 Bellman-Ford 요약

변형된 벨만 포드 알고리즘은 graph duplication을 통해 DAG 그래프를 생성하여 DAG relaxation으로 SSSP 문제를 $O(|V||E|)$ 시간에 풀었다. 또한 $s$로부터 $v$로 가는 경로에서 reachable한 negative weight cycle을 $\delta(s,v) = -\infin$으로 반환한다. 결국 시작은 일반적인 그래프였지만, DAG 그래프로 변형하여 DAG relaxation을 수행하였다. 이 강의가 기발하다고 생각하는 점이 여기에 있다. 하나의 기준틀을 제공해주고 개념을 확장시켜나가면서 기준틀을 바탕으로 개념을 엮는게 너무 좋다. 많은 강의들이 개념들을 단절된 형태로 ~가 있다. 방식으로 설명하는데에 갈증을 느꼈던 나로선 이런 깊이가 있는 사골같은 강의를 무료로 들을 수 있는 시대에 태어난 것에 감사하다.

4-2.2 변형된 Bellman-Ford vs 오리지널 Bellman-Ford

오리지널 벨만포드는 변형된 벨만포드와 비교해 장단점이 존재한다. 장점은 오리지널 벨만 포드는 $\delta(s_0, v_{k-1})$과 $\delta(s_0, v_k)$, $k \in \{1,...,|V|\}$만을 저장하여 $O(|V|)$ 공간만을 필요로 한다. 이는 단점이 될 수 있는데, $\delta(s_0, v_{k-1})$과 $\delta(s_0, v_k)$만을 저장하기 때문에 negative-weight cycle 포함 유무만을 판단 할 뿐, 자체를 반환하지 못한다.

4-2.3 오리지널 Bellman-Ford 알고리즘

• #1. 거리를 무한대로 초기화한다.
• #2. $|V|-1$ 횟수 안에 모든 edge를 relax한다.

def bellman_ford(Adj, w, s):
	# initialization
    infinity = float('inf')
    d = [infinity for _ in Adj]
    parent = [None for _ in Adj]
    d[s], parent[s] = 0, s
    # construct shortest paths in rounds
    V = len(Adj)
    for k in range(V - 1):
    	for u in range(V):
        	for v in Adj[u]:
            	try_to_relax(Adj, w, d, parent, u, v)
	# check for negative weight cycles accessible for s
    for u in range(V):
    	for v in Adj[u]:
        	if d[v] > d[u] + w(u,v):
            	raise Exception('There is a negative cycle!')
    return d, parent
            
            
def try_to_relax(Adj, w, d, parent, u, v):
	if d[v] > d[u] + w(u,v):
    	d[v] = d[u] + w(u,v)
        parent[v] = u

한마디로 요약하면, 벨만 포드 알고리즘은 relaxation 알고리즘과 같다. 다만, edge를 처리할 수 있는 순서를 제한하여 $|V|-1$ 번 안에 모든 edge relaxation을 마친다.