[MIT 6.006] 13. Dijkstra ( 다익스트라 )

Aacara·2023년 5월 31일

자료구조

자료구조 및 알고리즘

목록 보기

13/13

MIT 6.006 Introduction to Algorithms 20강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=NSHizBK9JD8&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=20

여태 배운 내용

Previously

9강 BFS, 11강 Weighted Shortest Paths, 12강 Bellman-Ford를 통해 weighted 그래프에 대한 SSSP(Single-Source Shortest Paths) 문제를 풀었다. 물론, 그래프의 형태, 일부 알고리즘은 수행하는 대상인 그래프의 가중치에 제약을 걸 때도 있었다.

SSSP(Single-Source Shortest Paths) 문제

$\textbf{O(|V|+|E|)}$ :
- 가중치가 양수이고 bounded되어 있는 경우 BFS로 품
- DAG 그래프의 경우 vertices를 topological order로 나열한 후, 가장 뒷단에 있는 노드부터 앞으로 나아가며 relaxation을 통해 가장 짧은 경로를 찾음
$\textbf{O(|V||E|)}$ : 음의 가중치를 가질 수 있는 일반적인 그래프에 대하여 벨만포드 알고리즘으로 품

Today

벨만 포드 알고리즘은 일반적인 그래프에 대하여 SSSP 문제를 풀 수 있다는 큰 장점이 있으나, $O(|V||E|)$ 시간이 걸린다는 단점이 있다. 만약 그래프 $G$ 가 sparse하다면, $E=O(V)$ 이므로 총 $E=O(V^2)$ 시간이 걸린다. 하지만 그래프 $G$ 가 dense하다면, $E=O(V^2)$ 이므로 총 $E=O(V^3)$ 시간이 걸린다. 실행시간에 세제곱근은 지양해야 할 요소다. 따라서, 비록 non-negative 가중치를 갖는 그래프라는 제약이 있지만 더 빠른 실행시간을 갖는 알고리즘인 다익스트라 알고리즘을 살펴본다. 실생활에서 음수의 가중치를 다루지 않는 경우가 더 많으므로 다익스트라 알고리즘이 벨만 포드에 비해 더 실용적이고 많이 사용된다.

1. Non-negative Edge Weights

다익스트라 알고리즘을 non-negative edge weights를 가지는 그래프에 한정해서 푸는 이유를 알아보자. 직관적으로는, 다익스트라는 가중치가 없는 그래프에 대해 적용하는 BFS 알고리즘을 가중치가 존재하는 그래프에 대해 일반화한 알고리즘이기 때문이다.

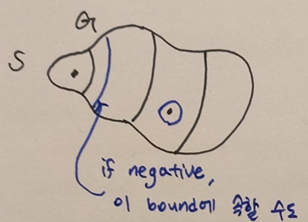
음수의 가중치를 가지면 안되는 이유를 증명하기 위해 먼저 다익스트라 알고리즘의 흐름을 간단히 살펴보자.

#1. 원천 노드 s를 중심으로 구를 키운다.
#2. 멀리 떨어진 정점을 탐색하기 전에 더 가까운 정점을 반복적으로 탐색한다.
#3. 주의! 하지만 거리를 미리 알지 못하는데 더 가까운 꼭짓점을 판단한다는 것은 모순이다.

Observation 1에서 음의 가중치를 가지는 그래프에 대해 다익스트라 알고리즘을 적용할 수 없는 이유를 알아본다. 그 다음, 꼭짓점들이 거리 증가순으로 주어진다는 가정을 했을 때 SSSP 문제를 빠르게 푸는 방법을 observation 2에서 제시한다.

Observation 1: 만약 weights $\geq 0$ 이라면, 최단 경로에서의 vertex를 지나갈 수록 거리가 증가한다. 즉, $\delta(s,u) \leq \delta(s,v)$ 이다.
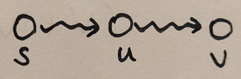
- $V_x \sub V$ 인 $V_x$ 는 원천 노드 s에서 $\leq x$ 거리 내에 도달할 수 있는 vertices의 부분 집합이다.
- $v \in V_x$ 일 때, $s$ 부터 $v$ 까지의 최단거리는 $V_x$ 에 있는 vertices만을 포함한다.
- $V_x$ 를 한번에 하나의 vertex만을 탐색하면서 점진적으로 늘린다.
  ※ 만약, 그래프에 음의 가중치가 존재한다면, vertex를 지나갈 수록 거리가 증가한다는 명제가 거짓이므로, $V_x$ 를 점진적으로 늘리는 접근 방식을 도입할 수 없다. $s$ 부터 $v$ 까지의 최단거리가 $V_x$ 에 있는 vertices가 아닌 $V_{x-\alpha},\ \alpha > 0$ 에 있는 vertices를 포함할 수 있기 때문이다.
Observation 2: 사전에, vertices가 거리 증가순으로 주어진다면 SSSP를 빨리 해결할 수 있다.

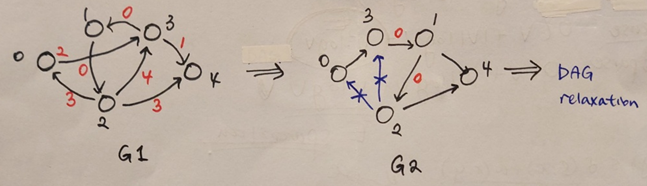
예시를 통해 DAG relaxation을 원활하기 위해 그래프를 변형하는 과정을 살펴보자. $G1$ 그래프의 경우 원천 노드 $s$ 로부터 증가하는 순서로 vertices의 순서가 부여되었다. 이러한 형태의 그래프에선 가중치가 0이 아닌 이상 어떠한 edge도 역행하지 않는다. Edge가 역행하면 topological order이 깨져 DAG relaxation을 수행할 수 없다. $G1$ 그래프와 같이 0 가중치에 의해 edge가 역행하는 경우 $G2$ 와 같이 0 가중치를 갖는 노드 간의 순서를 바꿔준다. 그 후 역행하는 edge $(2,0), (2,3)$ 을 삭제한다. 마지막으로, vertex 1,2,3을 병합하면 DAG relaxation을 수행할 수 있는 상태가 된다.

위의 과정을 요약해보자.

거리 증가순으로 주어진 vertices에서, 가중치가 0이 아님에도 역행하는 edges를 제거한다.
만약 가중치가 0인 edge가 주어진다면, vertices를 하나의 vertex로 병합한다.
DAG relaxation을 통해 모든 $v \in V$ 에 대한 $\delta(s,v)$ 를 계산한다. $O(|V|+|E|)$

Observation 2는 11.Weighted Shortest Paths에서 배운 DAG relaxation을 복습한 것과 다름이 없다. 자세한 내용을 위해선 다음 링크를 확인해보자. https://velog.io/@aacara/11.-Weighted-Shortest-Paths#3-2-dag-relaxation

2. Dijkstra's Algorithm

앞서 음이 아닌 가중치를 갖는 그래프에서 더 가까운 꼭짓점을 판단할 수 있다는 가정 하에 SSSP 문제를 우리에게 익숙한 DAG relaxation을 통해 풀었다. 하지만, #3. 거리를 미리 알지 못하는데 더 가까운 꼭짓점을 판단한다는 모순을 아직 해결하진 못했다. 다익스트라 알고리즘은 이에 대한 해결방법을 제시한다.

2.1 알고리즘

다익스트라 알고리즘은 원천 노드 $s$ 로부터 거리 증가순으로 edges를 relax한다. 다시 말해서, 하나의 vertex를 기준으로 edges를 relax하는 과정을 반복한다. 이때, 기준 vertex의 out-going edges 중 아직 relax되지 않은 edge를 relax하면서 가장 가중치의 합이 작은 경로를 구한다.

위의 과정을 수행하기 위해선, 거리가 증가하는 순서에서 다음으로 작은 노드가 무엇인지 찾을 수 있어야 한다. 이를 위해 Changeable Priority Queue라는 자료구조를 사용한다.

2.1-1. Changeable Priority Queue

연산	설명
$Q.build(X)$	iterator x에 있는 item들로 Q를 초기화
$Q.delete\_min()$	가장 작은 키값을 가진 item을 제거
$Q.decrease\_key(id,k)$	id를 가진 item을 찾은 후, 해당 item의 키값을 k로 바꿈

$Q.build(X)$ 나 $Q.delete\_min()$ 의 경우 기존의 우선순위 큐의 연산과 동일하다. $Q.decrease\_key(id,k)$ 연산 때문에 changeable이라는 단어가 붙은 것인데, 해당 id를 가진 item이 존재한다면 찾은 후, key값을 더 작은 값인 k로 바꾼다. 이러한 작업을 위해 추가적인 자료구조를 우선순위 큐와 함께 써야 한다.

추가적인 자료구조는 id 값과 priority queue에서의 위치를 매핑해야 한다. 이때, id값을 key로, priority queue에서의 위치를 item으로 생각한다면, 이 곧 key로 item들을 쿼리할 수 있도록 데이터를 저장하는 set interface이다. Hash table과 direct access array는 set interface에서 $find(k), insert(k), delete(k)$ 를 $O(1)$ 시간에 연산할 수 있는 자료구조다. $u$ 가 가장 큰 key의 값이고 $n$ 이 저장하고자 하는 item의 개수일 때, $u \gg n$ 면 메모리 공간을 너무 많이 차지하는 direct access array가 적합하지 않다. 그 대신, u space로부터 압축된 space로 span하는 hash table을 자주 사용한다. 하지만 이번 경우 id의 값이 $0 \sim |V|-1$ 이므로 $u=n$ 이다. 따라서, hash table이 아닌 direct access array를 사용해도 차지하는 메모리 공간에 큰 차이가 없다. 정리하자면, changeable priority queue 자료구조의 연산들을 수행하기 위해 priority queue와 dictionary를 cross-linking한다.

강의에서 hash table과 dictionary를 혼용해서 사용하곤 한다. 살짝 주제에 벗어나지만, 비슷하되 약간의 차이가 있는 자료구조들을 이번 기회에 잠시 정리하고 넘어가자. Hash table과 dictionary, array와 list의 사용법은 비슷하지만 내부 원리상의 차이가 있다. 내부 원리는 추후에 별도의 글로 작성하도록 하고 😊 일단 표면적인 차이점만 다룬다.

hash table vs dictionary

Hash table을 파이썬으로 구현한 자료구조가 dictionary다.

공통점: Hash table과 dictionary는 key-value 쌍을 저장하고 불러오는 자료구조다.
차이점: Hash table은 키를 값과 연결하기 위해 hash function과 array를 사용하는 데이터 구조이고, Dictionary는 키-값 쌍의 컬렉션을 나타내는 추상 데이터 타입이다. 따라서, hash table은 dictionary의 구체적인 구현으로 dictionary가 더 넓은 범위의 개념이다. 즉, Dictionary가 hash table의 상위호환 개념이다. 특징으로는, hash table은 key/value 쌍을 같은 타입 혹은 다른 타입으로도 저장할 수 있는 반면에 dictionary는 key/value쌍을 같은 타입으로 저장해야 한다.

array vs list

Array를 파이썬으로 구현한 자료구조가 list다. 물론, 파이썬의 내장 객체가 아닌 numpy 패키지를 이용하면 파이썬으로도 array 사용이 가능하다.

공통점: Array과 list는 모두 여러 데이터를 하나의 객체로 관리하기 위한 자료구조다. 파이썬 리스트의 경우, 연속된 메모리 공간에 저장하는 점도 array와 같다.
차이점: Array는 보통 static array를 의미하며 생성할 때 길이가 정해져 바뀌지 않는다. 그에 반해 list는 내부적으로 dynamic array를 구현하여 원소를 추가하거나 삭제할 때 길이가 바뀐다.

2.1-2. 알고리즘 단계

다시 본문으로 돌아와서 다익스트라 알고리즘의 과정을 살펴보자.

초기화: 모든 $v \in V$ 에 대하여 $d(s,v) = \infin$ 으로 설정, 원천 노드에 대해 $d(s,s) = 0$ 으로 설정한다.
Changeable priority queue $Q$ 를 생성: $Q$ 의 item은 모든 $v \in V$ 에 대하여 $(v, d(s,v))$
$Q$ 가 빈 상태가 아닐 동안, 가장 작은 $d(s,u)$ 를 가지는 $(u, d(s,u))$ item을 삭제한다.
- $d(s,v) > d(s,u) + w(u,v)$ 에 대하여:
  - Edge $(u,v)$ 를 relax한다.
    즉, $d(s,v) = d(s,u) + w(u,v)$ 로 설정한다.
  - $Q$ 에 있는 키값 $v$ 를 $d(s,v)$ 로 줄인다.

def dijkstra(Adj, w, s):
	d = [float('inf') for _ in Adj]
    parent = [None for _ in Adj]
    d[s], parent[s] = 0, s
    Q = PriorityQueue()
    V = len(Adj)
    for v in range(V):
    	Q.insert(v, d[v])
    for _ in range(V):
    	u = Q.extract_min()
        for v in Adj[u]:
        	try_to_relax(Adj, w, d, parent, u, v)
            Q.decrease_key(v, d[v])
    return d, parent
    
def try_to_relax(Adj, w, d, parent, u, v):
	if d[v] > d[u] + w(u,v):
    	d[v] = d[u] + w(u,v)
        parent[v] = u

과정을 보면 다익스트라 역시 벨만 포드처럼 relaxation 맥락에서 벗어나지 않는다. 강의가 DAG relaxation으로 부터 시작해서 벨만포드와 다익스트라에 이르러 relaxation이라는 기본틀로 설명하고 있다.

구체적인 예시를 통해 다익스트라 알고리즘이 전개되는 과정을 살펴보면 이해가 쉬워진다.

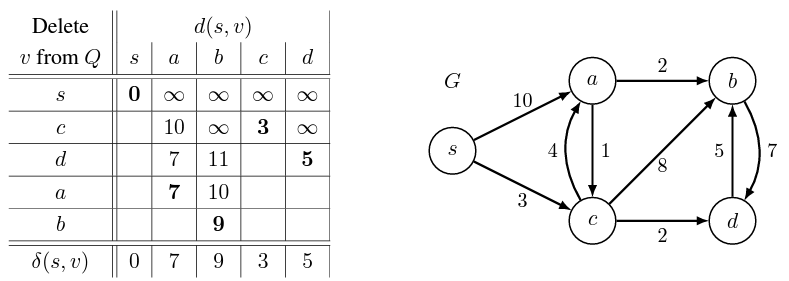
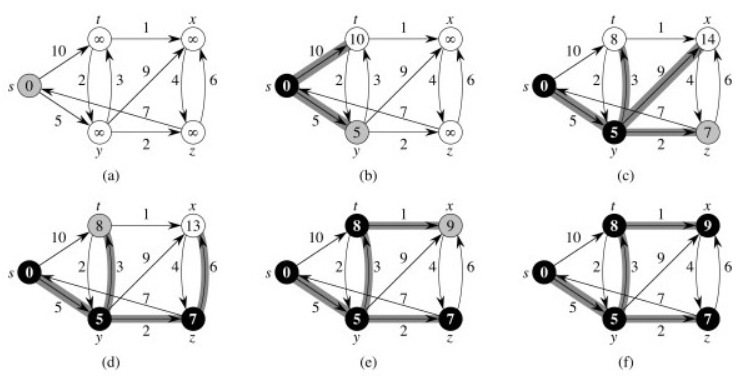
그래프 $G$ 의 모든 vertices s, a, b, c, d의 거리를 처음에 무한대로 모두 초기화한다. $d(s,s)=0$ 이므로 $Q$ 에서 $s$ 노드가 삭제된다. 그 후 $Adj(s) = \{a,c\}$ 에서 $d(s,a) = 10,\ d(s,c) = 3$ 을 구한다.

이때 가장 짧은 경로가 $d(s,c) = 3$ 이므로 $Q$ 에서 $c$ 노드를 삭제한다. $Adj(s) = \{a,b,d\}$ 에서 $d(s,a) = 7,\ d(s,b) = 11,\ d(s,d) = 5$ 을 구한다. 여기서, $d(s,a) = 10$ 보다 $7$ 이 작으므로 $d(s,a)$ 를 갱신한다. $d(s,b),\ d(s,d)$ 또한 $\infin$ 모다 작으므로 $d(s,b)$ 를 갱신한다.

이때 가장 짧은 경로가 $d(s,d) = 5$ 이므로 $Q$ 에서 $d$ 노드를 삭제한다. $Adj(d) = \{b\}$ 에서 $d(s,b) = 10$ 을 구한다. 이는 기존에 구했던 $d(s,b) = 11$ 보다 작으므로 $d(s,b)$ 을 갱신한다.

이때 가장 짧은 경로가 $d(s,a) = 7$ 이므로 $Q$ 에서 $a$ 노드를 삭제한다. $Adj(a) = \{b,c\}$ 에서 $d(s,b) = 9,\ d(s,c) = 8$ 을 구한다. $d(s,b) = 9$ 는 기존의 $d(s,b) = 10$ 보다 작기 때문에 갱신하나, $d(s,c) = 8$ 은 기존의 $d(s,c) = 3$ 이 더 크기 때문에 갱신하지 않는다.

마지막으로 남은 노드인 $b$ 를 $Q$ 에서 삭제하면 완료된다.

말로 표현하니 복잡해보일 수 있으나, changeable priority queue에서 모든 노드가 삭제될 때까지 같은 과정을 반복할 뿐이다.

2.2 Correctness

claim: 다익스트라 알고리즘을 끝까지 수행하면, 모든 $v \in V$ 에 대하여 $d(s,v)=\delta(s,v)$ 이다.
proof:
- Relaxation이 $d(s,v)$ 를 $\delta(s,v)$ 로 설정한다면, 알고리즘을 끝까지 수행했을 때 $d(s,v)=\delta(s,v)$
  - Relaxation은 $d(s,v)$ 를 감소할 수 있을 뿐, 증가시키진 않는다.
  - Relaxation은 safe하다.
    Safe하다의 뜻: $d(s,v)$ 가 $v$ 까지의 경로의 가중치의 합 혹은 $\infin$
- $v$ 가 $Q$ 에서 제거될 때, $d(s,v)=\delta(s,v)$ 이다. 를 보이는 것만으로도 충분하다. 역시 induction을 사용해서 증명한다.
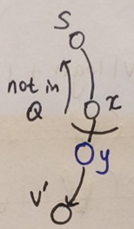
  - Induction: $Q$ 에 있는 처음 $k$ vertices가 제거되었다고 가정한다.
  - Base case(k=1): $s$ 는 $Q$ 에서 제거되는 첫번째 vertex, $d(s,s)=0=\delta(s,s)$
  - inductive step: $k < k'$ 에 대하여 참이라고 가정. $Q$ 에서 제거되는 $k'$ 번째 vertex를 $v'$ 라고 한다.
  - $w(\pi) = \delta(s,v')$ , 즉 $s$ 로부터 $v'$ 까지의 가장 짧은 경로 $\pi$ 를 고려한다.
  - $(x,y)$ 를 $y$ 가 첫 $k'-1$ 까지의 vertex에 없을 때, 최단경로 $\pi$ 의 첫 번째 edge라고 하자. 어쩌면 $y=v'$ 일 수도 있겠다.
  - $x$ 가 $Q$ 로부터 제거되었을 때, induction에 의해 $d(s,x) = \delta(s,x)$ 이다. $x$ 를 제거할 때 edge $(x,y)$ 를 relax 하면 다음과 같은 식이 성립한다.
    - $d(s,y) \leq \delta(s,x) + w(x,y)$
      $\qquad \qquad$ ※ 최단 경로의 하위 경로 역시 최단 경로이므로
      $\qquad \quad= \delta(s,y)$
      $\qquad \qquad$ ※ edge의 가중치가 음수가 될 수 없으므로
      $\qquad \quad\leq \delta(s,v')$
      $\qquad \qquad$ ※ relaxation은 safe하기 때문에, 다시 말해서최단 경로보다 일반 경로의 크기가 더 크기 때문에
      $\qquad \quad\leq d(s,v')$
      $\qquad \qquad$ ※ $Q$ 에 $k'$ 번째로 제거되는 vertex는 $v'$ 이다.라는 정의에 의해, $v'$ 은 $Q$ 에서 가장 짧은거리 $d(s,v')$ 을 갖기 때문에
      $\qquad \quad\leq d(s,y)$
    - 따라서, $d(s,v)=\delta(s,v)$ 을 증명하였다.

2.3 실행 시간

다익스트라 알고리즘의 실행 시간은 priority queue interface를 어떠한 자료구조를 사용해서 구현하는지에 따라 달라진다.

2.3-0 (Changeable) Priority Queue

실행 시간 분석을 위해 priority queue interface의 연산을 다익스트라 알고리즘에 각 연산이 얼마다 발생하는지와 함께 상기시킨다.

연산	설명	실행 시간	다익스트라에서 발생 빈도
$Q.build(X)$	iterator x에 있는 item들로 Q를 초기화	$B_n$	1
$Q.delete\_min()$	가장 작은 키값을 가진 item을 제거	$M_n$	$\\|V\\|$
$Q.decrease\_key(id,k)$	id를 가진 item을 찾은 후, 해당 item의 키값을 k로 바꿈	$D_n$	$\\|E\\|$

총 실행 시간은 $O(B_{|V|}+|V|M_{|V|}+|E|D_{|V|})$ 이다.

priority queue interface의 3가지 연산의 실행시간을 자료구조마다 살펴본다. 다만 이때, $Q.build(X)$ 는 모두 $n$ 시간이 걸리므로 나머지 연산들에 대해서만 다룬다.

$n=|V|=O(|E|)$ 에서 그래프의 특성에 따라 $O(|E|)$ 실행시간이 달라진다. 그래프가 dense하다면 $|E|=O(|V|^2)$ 이고 그래프가 sparse하다면 $|E|=O(|V|)$ 시간이 걸린다. 따라서, 두 가지 경우로 나눠서 총 실행시간을 분석해야 한다.

2.3-1 Array/Hash Table

가장 간단한 자료구조인 array나 hash table을 사용해서 priority queue를 구현할 수 있다. Array와 hash table 모두 최솟값을 찾기 위해 전체 item을 훑어야하브로 $Q.delete\_min()$ 에 $n$ 시간이 걸린다. 다만, 특정 index로, 혹은 key 원하는 item을 $O(1)$ 시간에 찾을 수 있다.

연산	실행 시간	다익스트라에서 발생 빈도
$Q.build(X)$	$n$	$1$
$Q.delete\_min()$	$n$	$\\|V\\|$
$Q.decrease\_key(id,k)$	1	$\\|E\\|$

총 실행시간은 $O(n+|V|n+|E|) = O(|V|+|V|^2+|E|) = O(|V|^2+|E|)$

dense: $|E|=O(|V|^2)$ 이므로 $O(|V|^2)$
sparse: $|E|=O(|V|)$ 이므로 $O(|V|^2)$

Hash table을 이용해서 (changeable) priority queue를 구현하는 코드는 다음과 같다.

class PriorityQueue:
	def __init__(self):
    	self.A = {}
        
    def insert(self, label, key):
    	self.A[label] = key
        
    def extract_min(self):
    	min_label = None
        for label in self.A:
        	if (min_label is None) or (self.A[label] < self.A[min_label].key):
            	min_label = label
            del self.A[min_label]
            return min_label
            
    def decrease_key(self, label, key):
    	if (label in self.A) and (key < self.A[label]):
        	self.A[label] = key

2.3-2 Binary Heap

Binary heap에서 $Q.delete\_min()$ 와 $Q.decrease\_key(id,k)$ 연산에 $logn$ 시간이 걸리는 이유는 8. Binary Heaps에 자세히 기술되어 있다. https://velog.io/@aacara/8.-Binary-Heaps

연산	실행 시간	다익스트라에서 발생 빈도
$Q.build(X)$	$n$	$1$
$Q.delete\_min()$	$logn_{(a)}$	$\\|V\\|$
$Q.decrease\_key(id,k)$	$logn$	$\\|E\\|$

총 실행시간은 $O(n+|V|logn+|E|logn) = O(|V|+|V|log|V|+|E|log|V|) = O(|V|log|V|+|E|log|V|)$

dense: $|E|=O(|V|^2)$ 이므로 $O(|V|^2log|V|)$
sparse: $|E|=O(|V|)$ 이므로 $O(|V|log|V|)$

Hash table을 이용해서 (changeable) priority queue를 구현하는 코드는 다음과 같다.

class Item:
	def __init__(self, label, key):
    	self.label, self.key = label, key
        
class PriorityQueue:
	def __init__(self):
    	self.A = []
        self.label2idx = {}
        
    def min_heapify_up(self, c):
    	if c == 0:
        	return
        p = (c-1) // 2
        if self.A[p].key > self.A[c].key:
        	self.A[c], self.A[p] = self.A[p], self.A[c]
            self.label2idx[self.A[c].label] = c
            self.label2idx[self.A[p].label] = p
            self.min_heapify_up(p)
            
    def min_heapify_down(self, p):
    	if p >= len(self.A):
        	return
            l = 2*p + 1
            r = 2*p + 2
            if l >= len(self.A):
            	l = p
            if r >= len(self.A):
            	r = p
            c = l if self.A[r].key > self.A[l].key else r
            if self.A[p].key > self.A[c].key:
            	self.A[c], self.A[p] = self.A[p], self.A[c]
            	self.label2idx[self.A[c].label] = c
            	self.label2idx[self.A[p].label] = p
            	self.min_heapify_up(p)
                
    def insert(self, label, key):
    	self.A.append(Item(label, key))
        idx = len(self.A) - 1
        self.label2idx[self.A[idx].label] = idx
        self.min_heapify_up(idx)
        
    def extract_min(self):
    	self.A[0], self.A[-1] = self.A[-1], self.A[0]
        self.label2idx[self.A[0].label] = 0
        del self.label2idx[self.A[-1].label]
        min_label = self.A.pop().label
        self.min_heapify_down(0)
        return min_label
        
    def increase_key(self, label, key):
    	if label in self.label2idx:
        	idx = self.label2idx[label]
            if key < self.A[idx].key:
            	self.A[idx].key = key
                self.min_heapify_up(idx)

2.3-3 Fibonacci Heap

Fibonacci heap에 대한 내용은 심화 내용에서 6.006에서 다루지 않는다. 결과가 이렇다로만 알아두면 될 것 같다.

연산	실행 시간	다익스트라에서 발생 빈도
$Q.build(X)$	$n$	$1$
$Q.delete\_min()$	$logn_{(a)}$	$\\|V\\|$
$Q.decrease\_key(id,k)$	$1_{(a)}$	$\\|E\\|$

총 실행시간은 $O(n+|V|logn+|E|) = O(|V|+|V|log|V|+|E|) =O(|V|log|V|+|E|)$

dense: $|E|=O(|V|^2)$ 이므로 $O(|V|^2)$
sparse: $|E|=O(|V|)$ 이므로 $O(|V|log|V|)$

2.3-4. 자료구조 비교 및 분석

자료구조	dense 실행시간	sparse 실행시간
array/hash table	$O(\\|V\\|^2)$	$O(\\|V\\|^2)$
binary heap	$O(\\|V\\|^2log\\|V\\|)$	$O(\\|V\\|log\\|V\\|)$
fibonacci heap	$O(\\|V\\|^2)$	$O(\\|V\\|log\\|V\\|)$

표를 보면 dense한 그래프에서 array/hash table을 이용하고 sparse한 그래프에선 binary heap를 사용하는 것이 효과적임을 확인할 수 있다. Fibonacci heap를 사용한다면 그래프가 dense한지 sparse한지에 상관없이 최적의 실행시간을 가진다. 다만 구현하는 것이 다소 까다롭다. 실제로는 SSSP 문제를 풀기 위해 알고리즘을 사용하기 전, 그래프가 dense한지 sparse한지 알고 있는 경우가 대부분이므로 그래프의 특성에 따라 구현하기 비교적 용이한 array/hash table 혹은 binary heap를 사용하자.

Aacara

https://github.com/aacara

이전 포스트