[MIT 6.006] 3. Sorting ( 정렬 )

Aacara·2023년 3월 23일

자료구조

자료구조 및 알고리즘

목록 보기

3/13

MIT 6.006 Introduction to Algorithms 4강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=oS9aPzUNG-s&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=4

4강에서 다룰 interface와 data structure

interface: set

data structure: array, sorted array

P. Set Interface

2강에서 Sequence는 extrinsic한 순서로 collection of items의 순서가 유지된다는 것을 배웠다. 그에 반해 set은 intrinsic한 순서로 collection of items가 저장된다. Intrinsic한 순서로 배치되었다는 것은 각 item 자체의 특성이 의미가 있다는 뜻이다. Array, sorted array의 경우 특성의 범위를 item 자체의 값으로 한정해서 다루지만, item의 key로 확장될 수도 있다. 혹은, 이렇게도 이해해볼 수 있다. 결국 set interface는 key값으로 순서를 정하지만 array, sorted array의 경우 item값 자체를 key 값으로 삼는 것이다. 또한 자체의 특성이 의미가 있으려면 그 특성의 대상, (item 자체의 값 또는 key)는 중복이되어선 안된다.

Set interface에서 가능한 operation들은 다음과 같다.

종류	operation	설명
container	build(X)	iterable X가 주어졌을 때 X의 item들로 sequence를 만듦
	len()	저장되어 있는 item의 수 $n$ 을 반환
static	find(k)	key가 k인 값을 반환
dynamic	insert(x)	x를 set에 추가(x.key가 이미 있다면 기존의 값을 대체)
	delete(k)	key가 k인 item을 삭제하고 저장되어 있는 item을 반환
order	iter_ord()	key의 순서에 따라 저장되어 있는 item들을 하나씩 반환
	find_min()	가장 작은 key값의 item을 반환
	find_max()	가장 큰 key값의 item을 반환
	find_next(k)	k보다 큰 key값들 중 가장 작은 key값을 가진 item을 반환
	find_prev(k)	k보다 작은 key값들 중 가장 큰 key값을 가진 item을 반환

p-s1. array

Set interface의 operation들을 수행할 데이터 구조로 sequence에서 사용했었던 array를 가장 먼저 떠올려본다. Array의 경우 메모리의 연속적인 공간에 item을 저장한다. 하지만 무질서하게 item을 저장한 array는 그 값들에 intrinsic한 의미를 담고 있지 못한다. 따라서, $find(x)$ 와 같은 연산을 수행할 때 최대 n개의 원소를 모두 살펴봐야하므로 $O(n)$ 시간이 걸린다. 그 뿐만 아니라, 다른 연산들에 대해서도 $O(n)$ 시간이 소요된다. 데이터셋의 크기가 기하급수적으로 커진다면 item을 찾는데 $O(n)$ 시간이 걸린다는 것은 매우 비효율적이다.

종류	operation	$O()$
container	build(x)	$O(n)$
static	find(k)	$O(n)$
dynamic	insert(x)	$O(n)$
	delete(k)	$O(n)$
order	find_min()	$O(n)$
	find_max()	$O(n)$
	find_next(k)	$O(n)$
	find_prev(k)	$O(n)$

p-s2. sorted array

만약 무질서한 array를 질서있게 만든다면 어떨까? 그떄서야 비로소 array의 item들의 intrinsic한 의미를 살릴 수 있게 된다.

$find\_min(), find\_max()$ 는 $O(1)$ 시간이 걸릴 것이다. $find(k)$ 의 경우 $O(logn)$ 시간이 걸리는데 sorted array의 경우 이진 탐색(binary search)가 가능해지기 때문이다. $build(X)$ 의 경우 $O(nlogn)$ 시간이 걸리는데 이는 추후에 증명한다.

$find(x), find\_min(), find\_max()$ 연산에 대하여 sorted array는 그냥 array에 비해 성능이 좋다는 것을 확인하였다. 비록 $build(X)$ 연산에는 $O(nlogn)$ 시간이 걸려 그냥 array를 생성할 때 걸리는 시간인 $O(n)$ 보다 비효율적이지만, 한 번 오래 걸려서 잘 만들어놓고 쉽게 찾는 것이 더 나을 때가 많다. Array를 sort하는 것이 중요하다는 것을 확인하였으므로 이제 여러 sorting 방법을 비교해보고 가장 효율적인 방법을 찾아볼 것이다.

종류	operation	$O()$
container	build(x)	$O(nlogn)$
static	find(k)	$O(logn)$
dynamic	insert(x)	$O(n)$
	delete(k)	$O(n)$
order	find_min()	$O(1)$
	find_max()	$O(1)$
	find_next(k)	$O(n)$
	find_prev(k)	$O(n)$

class Sorted_Array_Set:
	def __init__(self):            	    # O(1)
    	self.A = Array_Seq()
    def __len__(self):                  # O(1)
    	return len(self.A)
    def __iter__(self):                 # O(n)
    	yield from self.A
    def iter_order(self):               # O(n)
    	yield from self
        
    def build(self, X):                 # O(?)
    	self.A.build(X)
        
    def _sort(self):                    # O(?)
    	??
        
    def _binary_search(self, k, i, j):  # O(log n)
    	if i >= j:
        	return i
        m = (i + j) // 2
        x = self.A.get_at(m)
        if x.key > k:
        	return self._binary_search(k, i, m - 1)
        if x.key < k:
        	return self._binary_search(k, m + 1, j)
        return m
        
    def find_min(self):                 # O(1)
    	if len(self) > 0:
        	return self.A.get_at(0)
        else:
        	return None
            
    def find_max(self):                 # O(1)
    	if len(self) > 0:
        	return self.A.get_at(len(self) - 1)
        else:
        	return None
            
    def find(self, k):                  # O(log n)
    	if len(self) == 0:
        	return None
        i = self._binary_search(k, 0, len(self) - 1)
        x = self.A.get_at(i)
        if x.key == k:
        	return x
        else:
        	return None
            
    def find_next(self, k):             # O(log n)
    	if len(self) == 0:
        	return None
        i = self._binary_search(k, 0, len(self) - 1)
        x = self.A.get_at(i)
        if x.key > k:
        	return x
        if i + 1 < len(self):
        	return self.A.get_at(i + 1)
        else:
        	return None
        
    def find_prev(self, k):
    	if len(self) == 0:
        	return None
        i = self._binary_search(k, 0, len(self) - 1)
        x = self.A.get_at(i)
        if x.key < k:
        	return x
        if i > 0:
        	return self.A.get_at(i-1)
        else:
        	return None
    
    def insert(self, x):
    	if len(self.A) == 0:
        	self.A.insert_first(x)
        else:
        	i = self._binary_search(x.key, 0, len(self.A) - 1)
            k = self.A.get_at(i).key
            if k == x.key:
            	self.A.set_at(i, x)
                return False
            if k > x.key:
            	self.A.insert_at(i, x)
            else:
            	self.A.insert_at(i + 1, x)
        return True
        
    def delete(self, k):
    	i = self._binary_search(k, 0, len(self.A) - 1)
        assert self.A.get_at(i).key == k
        return self.A.delete_at(i)

Sorting

Set interface에 array data structure를 사용하려면 sorting을 하는 것이 효율적임을 앞에서 확인하였다. 그렇다면 sorting을 정의 내려보자.

sorting

Input: $n$ 개의 숫자에 대한 $static\ array$

Output: 오름차순으로 나열된 A의 permutation 중 하나인 array B
- Permutation: 같은 원소들을 각자 다른 순서로 나열한 array, 순열

Sorted: $B[i-1] \leq B[i]$ for all $i \in \{1, ..., n\}$

앞서, sorted array는 $build(X)$ 를 연산하는데에 $O(nlogn)$ , $find(k)$ 를 연산하는데에 $O(logn)$ 시간이 걸린다고 하였다. 이는 sorting 방법 중 가장 효율적인 sorting 방법을 도입했을 때의 경우다. 여러가지 sorting 방법을 비교,분석해서 $build(X)$ 연산을 가장 효율적으로 수행하는 sorting 방법을 찾아보자.

1. permutation sort

Permutation sort는 가장 쉽게 떠올릴 수 있는 sorting 방법으로 가능한 모든 수의 나열 중 sorting된 나열을 찾는 방법이다.

모든 permutation들을 나열한다. $\Omega(n!)$

나열되어 있는 permutation들 중 순서대로 나열되어있는 순열을 찾아낸다. $O(n)$

def permutation_sort(A):
	'''Sort A'''
    for B in permutations(A):     # O(n!)
    	if is_sorted(B):          # O(n)
        	return B              # O(1)

결국 permutation_sort의 $build(X)$ 에 $\Omega(n!n)$ 시간이 소요되므로 비효율적이다.

2. selection sort

Selection sort는 다음과 같은 방법으로 진행된다.

$A[:i + 1]$ 에서 가장 큰 수를 찾는다.

가장 큰 수와 $A[i]$ 와 바꾼다.

recursive하게 $A[:i]$ 를 정렬한다.

예시
8 2 4 9 3
8 2 4 3 9
3 2 4 8 9
3 2 4 8 9
2 3 4 8 9

# 2. 가장 큰 수와 $A[i]$와 바꾼다.
# 3. recursive하게 $A[:i]$를 정렬한다.
def selection_sort(A, i = None):      # T(i)
	'''Sort A[:i + 1]'''
    if i is None:                     # O(1)
    	i = len(A) - 1
    if i > 0:                         # O(1)
    	j = prefix_max(A, i)          # S(i)
        A[i], A[j] = A[j], A[i]       # O(1)
        selection_sort(A, i - 1)      # T(i - 1)

# 1. A[:i + 1]에서 가장 큰 수를 찾는다. 
def prefix_max(A, i):                 # S(i)
	'''Return index of maximum in A[:i + 1]'''
    if i > 0:                         # O(1)
    	j = prefix_max(A, i - 1)      # S(i - 1)
        if A[i] < A[j]:               # O(1)
        	return j                  # O(1)
    return i

prefix_max(A, i)

1강에서 배웠던 induction을 통한 correctness를 증명해보자.

$S(n): prefix\_max(A, i)$ 를 수행하는 연산량

Base case: i = 0에서 하나의 원소 뿐이므로 가장 큰 원소는 i
$S(1) = O(1)$
Induction:
$S(n) = S(n - 1) + O(1)$

가정: $S(n) = cn$

$cn = c(n - 1) + O(1)$
$\sout{cn} = \sout{cn} - c + O(1)$
$c = O(1)$ 이므로 $S(n) = cn$ 가정은 참
- n개의 node에 대하여 recurrence가 일어나므로 $\displaystyle\sum_{i=0}^{n-1}c = cn \simeq O(n)$

따라서, $A[:i + 1]$ 에서 가장 큰 수를 찾는 $predix\_max(A, i)$ 연산의 연산량 $S(n) = O(n)$ 이다.

selection_sort(A, i)

$T(n): selection\_sort(A, i)$ 를 수행하는 연산량

Base case: i = 0에서 하나의 원소 뿐이므로 sorted 되어있음
$T(1) = O(1)$
Induction:
$T(n) = T(n - 1)(직전의 selection\_sort) + O(n)(prefix\_max)$
$cn^2$
가정: $T(n) = cn^2$
- n개의 node에 대하여 recurrence가 일어나므로 $\displaystyle\sum_{i=0}^{n-1}n =$ ${n(n-1)}\over2$ $\simeq O(n^2)$
$cn^2 = c(n - 1)^2 + O(n)$
$\sout{cn^2} = \sout{cn^2} - 2cn + c + O(n)$
$O(n) = 2cn - c$ 이므로 $T(n) = cn^2$ 가정은 참

정리하자면, selection_sort의 $build(X)$ 에 $O(n^2)$ 시간이 소요되므로 가장 효율적인 sorting 방법이 아니다.

3. insertion sort

Insertion sort의 원리는 selection sort와 비슷하다. 다만, array A의 오른쪽부터 큰 원소를 나열하는 방식이 아닌 array A의 왼쪽부터 작은 원소를 나열하는 방식으로 sorting을 진행한다. Insertion sort 역시 $build(X)$ 에 $O(n^2)$ 시간이 소요되므로 자세한 correctness 증명은 생략한다.

Insertion sort와의 차이점을 이해하기 위해 insertion sort에 대해 조금 더 자세히 설명해보고자 한다. Insertion sort는 각 반복에서 하나의 요소를 취하여 그 요소가 올바른 위치에 들어갈 때까지 이전 요소들과 비교하여 이동한다. 다시 말해서, insertion으로 불리는 이유가 각 요소가 이미 정렬된 배열 부분에 삽입되기 때문이다.

recursive하게 $A[:i]$ 를 정렬한다.

$A[:i]$ 까지 정렬되었다는 전제하에 $A[:i + 1]$ 를 정렬한다.

예시
8 2 4 9 3
2 8 4 9 3
2 4 8 9 3
2 4 8 9 3
2 3 4 8 9

# 1. recursive하게 A[:i]를 정렬한다.
def insertion_sort(A, i = None):      
	'''Sort A[:i + 1]'''
    if i is None:
    	i = len(A) - 1
    if i > 0:
    	insertion_sort(A, i - 1)
        insert_last(A, i)
        
# 2. A[:i]까지 정렬되었다는 전제하에 A[:i + 1]를 정렬한다.       
def insert_last(A, i):
	'''Sort A[:i + 1] assuming sorted A[:i]'''
    if i > 0 and A[i] < A[i - 1]:
    	A[i], A[i - 1] = A[i - 1], A[i]
        insert_last(A, i - 1)

4. merge sort

Merge sort는 다음과 같은 방법으로 진행된다.

전제: list의 길이가 2의 배수

Recursive하게 첫 번째 반토막과 두 번째 반토막을 정렬한다.

두 개의 정렬된 반토막을 merge 한다.

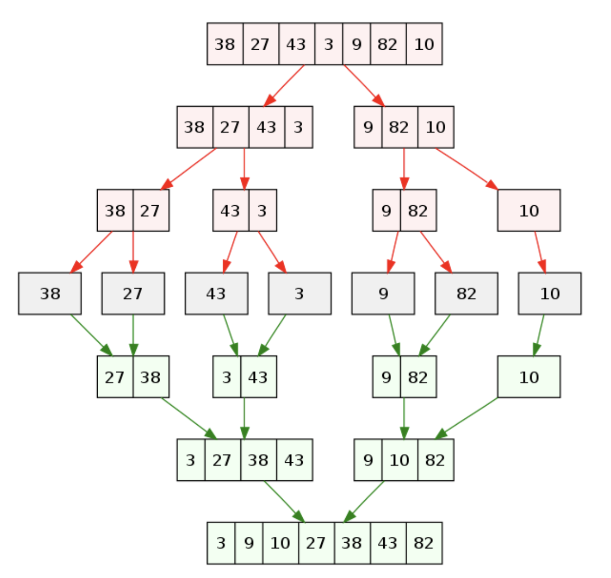
# 1. Recursive하게 첫 번째 반토막과 두 번째 반토막을 정렬한다.
def merge_sort(A, a = 0, b = None):           # T(b - a = n)
	'''Sort A[a:b]'''
    if b is None:                             # O(1)
    	b = len(A)                            
    if 1 < b - a:                             # O(1)
    	c = (a + b + 1) // 2                  # O(1)
        merge_sort(A, a, c)                   # T(n / 2)
        merge_sort(A, c, b)                   # T(n / 2)
        L, R = A[a:c], A[c:b]                 # O(n)
        merge(L, R, A, len(L), len(R), a, b)  # S(n)
        
# 2. 두 개의 정렬된 반토막을 merge 한다.        
def merge(L, R, A, i, j, a, b):
	'''Merge sorted L[:i] and R[:j] into A[a:b]'''
    if a < b:                                              # O(1)
    	if (j <= 0) or (i > 0 and L[i - 1] > R[j - i]):    # O(1)
        	A[b - 1] = L[i - 1]                            # O(1)
            i = i - 1                                      # O(1)
        else:                                              # O(1)
        	A[b - 1] = R[j - 1]                            # O(1)
            j = j - 1                                      # O(1)
        merge(L, R, A, i, j, a, b - 1)                     # S(n - 1)

merge

$S(n): merge(L, R, A, i, j, a, b)$ 를 수행하는 연산량

Base case: n = 0에 대하여 array는 비어있기 때문에 참
$S(0) = O(1)$
Induction: 2. selection sort에서의 prefix_max(A, i)와 동일
$S(n) = S(n - 1) + O(1)$

가정: $S(n) = cn$

$cn = c(n - 1) + O(1)$
$\sout{cn} = \sout{cn} - c + O(1)$
$c = O(1)$ 이므로 $S(n) = cn$ 가정은 참
- n개의 node에 대하여 recurrence가 일어나므로 $\displaystyle\sum_{i=0}^{n-1}c = cn \simeq O(n)$

merge_sort

$T(n): merge\_sort(A, a = 0, b = None)$ 를 수행하는 연산량

Base case: n = 1에 대하여 하나의 원소 뿐이므로 참
$T(1) = O(1)$
Induction:
$T(n) = 2T(\frac{n}{2})(직전의 merge\_sort) + O(n)(merge)$

가정: $T(n) = cnlogn$

$cnlogn = 2c\frac{n}{2}log\frac{n}{2} + O(n)$
$\sout{cnlogn} = cn(\sout{logn} - log2) + O(n)$
$O(n) = cnlog2 = (clog2)n \simeq O(n)$ 이므로 $T(n) = cnlogn$ 가정은 참