[MIT 6.006] 4. Hashing ( 해시 )

Aacara·2023년 3월 27일

자료구조

자료구조 및 알고리즘

목록 보기

4/13

MIT 6.006 Introduction to Algorithms 5강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=Nu8YGneFCWE&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=5

5강에서 다룰 interface와 data structure

interface: set

data structure: direct access array, hash table

P. Set Interface: O(logn) find(k) 증명

Interface를 다시 정리해본다.

Interface

set: key로 item들을 쿼리할 수 있도록 데이터를 저장하는 방법

sequence: external한 순서로 item을 저장하는 방법

지난 4강에선 set interface의 연산들을 수행하기 위해 sorted array를 도입하였다. 그 과정에서 여러 sorting 방법을 살펴본 결과, merge sort가 $find(k)$ 를 $O(logn)$ 시간으로 도입할 수 있어서 가장 효율적이었다. 그렇다면 $find(k)$ 를 $O(logn)$ 보다 더 빨리 도입할 순 없을까? 정답부터 말하자면, restricted computational model에서는 $O(logn)$ 이 최선이다. 또한, $find(k)$ 에 이어 두 번째로 최적화할 연산은 $insert(x), delete(k)$ 와 같은 동적 연산이다.

Comparison Model <- model of computation

Comparison Model

앞서, sorted array에선 $find(k)$ 를 수행하는 시간으로 $O(logn)$ 이 최선임을 증명하였다. 여기서 말한 restricted computational model은 comparison model이며 이러한 모델의 어떠한 특성 때문에 $O(logn)$ 이 최선인지 살펴보자.

Comparison model에서 item을 식별하는 유일한 방법은 비교다. 구체적으로 $\lt, \leq, \gt, \geq, =, \neq$ 와 같은 비교를 하고 결과는 True/False로 나타난다. 더 자세한 이해를 위해 decision tree를 보면서 이해하자.

Decision Tree

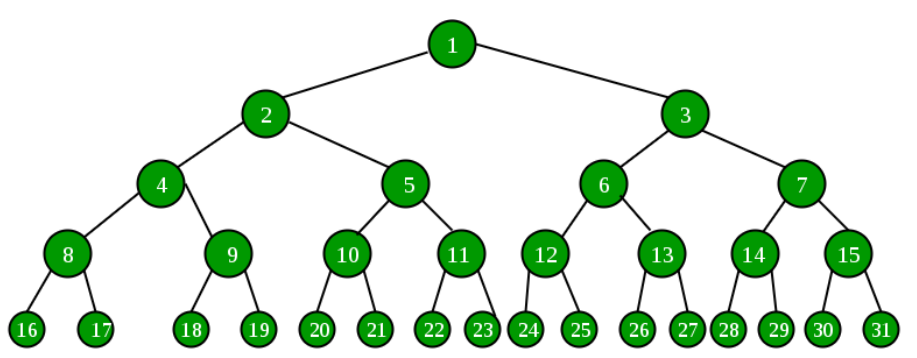
출처: https://www.geeksforgeeks.org/print-middle-level-perfect-binary-tree-without-finding-height/

우선, 각 item을 서로 다른 key를 가지고 있다고 가정한다. 이러한 가정 아래 탐색 알고리즘인 $find(k)$ 는 n개의 item이 있다고 할 때, 입력된 key와 같은 key를 가진 item을 반환하거나 찾는 값이 없다면 아무것도 반환하지 않을 것이다. 따라서 n+1개의 leaves(가장 하단에 위치한 노드들)가 존재한다. 참고로 각 노드는 알고리즘의 비교를 의미한다. 입력이 주어지면 탐색 알고리즘은 root 노드에서 시작하여 leaf에 도달할 때까지 노드를 거치면서 비교를 한다. 그렇기 때문에 worst-case number of comparisons는 decsision tree의 높이와 같다.

decision tree의 높이는 완벽하게 대칭을 이룰 때 가장 짧다. 완벽하게 대칭을 이룬다는 것은 root 노드로부터 늘 양갈래로 나뉜다는 것이고 위와 같은 그림에선, root 노드로부터 모든 leaf까지의 거리가 같다는 것을 의미한다.

완벽히 대칭인 상황에서, n개의 leaves는 root 노드로부터 높이가 하나씩 늘어날 때마다 2배
$2^{decision\ tree의 높이} = n$
$decision\ tree의 높이 = log_2n$

이로써 comparison model에서 $find(k)$ 를 $O(logn)$ 보다 빠르게 연산을 수행할 수 없음을 증명해냈다.

p-s1. Direct Access Array

그렇다면 $find(k)$ 를 $O(logn)$ 보다 빠르게 연산을 수행할 수 있는 comparison model이 아닌 다른 computational model를 찾아보자.
대부분의 comparison model은 상수의 branching factor를 가진다. 위에서 예시를 든 decision tree는 branching factor가 2였을 뿐이다. 만약에 branching factor가 고정된 값이 아니라 필요한만큼 늘어날 수 있다면 어떨까? 만약 선형적인 branching factor가 가능하다면, key값과 일치하는 index에 값을 저장할 수 있다. 예를 들어, x.key = 10이라면 메모리의 10번째 위치에 x값을 저장하는 것이다. 이러한 자료구조를 direct access array라고 한다.

잠시 정리하자면, Direct access array는 static array의 일종이지만 key 값에, sorted array는 item 값에 따라 intrinsic하게 배열 내 순서를 정한다.

Direct access array는 $find(k)$ 에 $O(1)$ 시간이 소요된다. Key 값이 곧 배열에서의 위치와 같기 때문이다. 결국 set interface의 $find(k)$ 연산을 수행하는 데에 있어서 $O(logn)$ 가 걸리는 sorted array 보다 빠른 Direct access array라는 자료구조를 찾은 셈이다. 추가적인 장점으로는 $insert(x), delete(k)$ 와 같은 동적 연산 또한 key값을 알면 바로 수행할 수 있기 때문에 $O(1)$ 시간이 소요된다.

Direct access array는 $find(k), insert(x), delete(k)$ 을 수행하는 데에 시간적인 장점이 있지만, $u\gg n$ 이라면 공간 사용이 매우 비효율적이다. $u\gg n$ 인 상황을 예시로 들면 대학 강의실에 있는 학생 수가 50명인데, 학번이 $10^6$ 까지 있는 상황이다. 50명( $n$ )만 저장하면 되는데 저장하기 위해 $10^6(u)$ 메모리 공간이 필요한 것이다. 결국, 시간과 메모리 공간은 tradeoff 관계에 있다.

$u$ : 가장 큰 key 값

$n$ : 저장하고자 하는 item의 개수

class DirectAccessArray:
	def __init__(self, u):                           # O(u)
    	self.A = [None] * u
    def find(self, k):                               # O(1)
    	return self.A[k]
    def insert(self, x):                             # O(1)
    	self.A[x.key] = x
    def delete(self, k):                             # O(1)
    	self.A[k] = None
    def find_next(self, k):                          # O(u)
    	for i in range(k, len(self.A)):
        	if A[i] is not None:
            	return A[i]
    def find_max(self):                              # O(u)
    	for i in range(len(self.A) - 1, -1, -1):
        	if A[i] is not None:
            	return A[i]
    def delete_max(self):                            # O(u)
    	for i in range(len(self.A) - 1, -1, -1):
        	x = A[i]
            if x is not None:
            	A[i] = None
                return x

p-s2. Hashing

Direct access array는 자칫하면 엄청난 메모리 공간을 필요로 한다는 단점이 있다. 공간적인 제약을 제거하면서 direct access array처럼 빠르게 원소에 접근할 수 있도록 하는 자료구조가 Hash table이다. Hash function은 key space $\{0,...,u-1\}$ 까지의 큰 u space로부터 compressed space $\{0,...,m-1\}$ 로 span한다. 이때, $u\gg m$ 이기 때문에 메모리 공간 효율이 향상된다. 하지만 큰 공간에 있던 원소들이 작은 공간에 밀집되면서 key space에선 다른 위치에 있던 두 원소가 compressed space에서는 같은 위치에 존재하는 경우가 생긴다. 수식으로 표현하면 $k1, k2 \in \{0, ..., u-1\}$ 일 때 $h(k1) = h(k2)$ 인 경우가 생기는 것이다. 이러한 상황을 collision이라고 한다.

Collision을 해결하는 방법으로는 크게 두 가지가 있다.
첫 번째 방법은 Open addressing으로 collision이 일어날 때마다 다른 비어 있는 공간을 찾아 그곳에 $u$ 공간의 key값을 저장한다. 가장 흔히 쓰이는 방법이지만 분석하기 어려우므로 개념만 알고 간다.

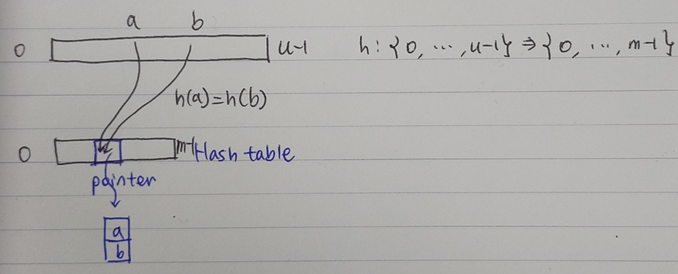
Chaining

두번째 방법은 chaining이다. Chaining은 충돌하는 key를 $\{0, ..., m-1\}$ hash table이 아닌 다른 자료 구조에 저장한다. 이때, $\{0, ..., m-1\}$ hash table에서 key값을 저장하던 공간은 새로운 자료 공간이 어디에 위치해 있는지 가르키는 pointer 역할을 하게 된다.

Chain의 크기는 작은 것이 이상적이다. $find(k), insert(x), delete(k)$ 연산을 하기 위해 새로운 자료 공간을 탐색해야하기 때문이다. 만약 key값들이 고르게 분포된다면 chain의 크기는 ${n\over m} = O(1)$ 이 된다. 고로, direct access array처럼 $O(1)$ 시간이 소요되므로 시간적 효율성이 뛰어나다.

하지만, $find(k), insert(x), delete(k)$ 연산에 $O(1)$ 시간이 소요되는 상황은 언제까지나 이상적인 경우에 한정된다. 최악의 경우, $u$ 공간에 있는 모든 key값이 $m$ 공간의 같은 위치에 몰릴 수 있다. 이때는 $find(k), insert(x), delete(k)$ 연산에 $O(n)$ 시간이 소요되어 sorted array보다 비효율적이다.

따라서, chain에 hash된 key의 갯수가 적은 hash function이 곧 좋은 hash function이다.

Division hash function

좋은 hash function을 고르기 전에 가장 떠올리기 쉽고 간단하지만, 좋지 않은 hash function인 division hash function을 먼저 살펴본다. $u$ 크기의 공간에서 $m$ 크기의 공간으로 mapping하기 가장 간단한 방법은 key를 m으로 나눈 나머지로 mapping하는 modulus다.

division hash function

h(k) = k mod m

다만, 이 방법에서 chain이 작으려면 key가 $u$ 공간에서 균등하게 분포되어 있어야 한다. 그에 반해 만약 모든 key의 나머지가 같다면 chain의 크기는 $u$ 공간에 있던 key값과 같을 것이다. 결국 Division hash function의 성능은 $u$ 공간에 있는 key 값에 종속적이다. 하지만 우리는 key값에 독립적인 hash function을 찾고 싶다.

Universal hash function

Universal hash function은 key값으로부터 독립성을 부여하기 위해 division hash function에 임의성 및 확장성을 추가한 개념이다. 여기서 말하는 임의성이란 고정된 hash function을 쓰는 대신 hash function들의 큰 집합으로부터 임의로 하나의 hash function을 고르는 것이다. 물론 이 경우에도 우연히, 안좋은 hash function을 고를 수도 있다. 하지만 충분히 많은 경우의 수의 기댓값을 구해보면 universal hash function의 성능이 좋다는 것을 알 수 있다.

universal hash function

$H(m, p)$ = $\{h_{ab}(k) = (((ak+b)\ mod\ p)\ mod\ m)\ a,b \in \{0, ..., p-1\}\ and\ a \neq 0\}$

$H(m, p)$ : hash family

$p$ : key 도메인 u보다 큰 소수

위와 같이 a와 b의 값을 고른다면 hash function 집합으로부터 하나의 고정된 hash function을 고를 수 있다. 여기서 어떠한 두 개의 key에 대해서도 hash들이 collision을 일으킬 확률이 $1 \over m$ 을 넘진 않는다. 그 이유는 수식 1번에서 알 수 있듯이 마지막에 $mod\ m$ , 즉 m으로 나눈 나머지를 mapping했기 때문이다.

$Pr_{h \in H}\{h(k_i) = h(k_j) \leq {1\over m}\}$

앞서 충분이 많은 경우의 수의 기댓값을 구해보면 universal hash function의 성능이 좋다고 했다. 여기서 말하는 성능이 좋다의 의미는 chain에 hash된 key의 갯수가 적다는 것이다. 이를 수식으로 증명해본다.

Universality

index $h(k_i)$ 에 저장된 hash된 key 갯수의 기댓값
$E_{h \in H}\{X_i\} = E_{h \in H}\{\displaystyle\sum_jX_{ij}\}$
= $\displaystyle\sum_jE_{h \in H}\{X_{ij}\} = 1 + \displaystyle\sum_{j \neq i}E_{h \in H}\{X_{ij}\}$
= $1 + \displaystyle\sum_{j \neq i}(1)Pr_{h \in H}\{h(k_i) = h(k_j)\} + (0)Pr_{h \in H}\{h(k_i) \neq h(k_j)\}$
$\leq1 +\displaystyle\sum_{j \neq i}(1)*{1 \over m} + (0)*{(1-{1 \over m})}$
= $\displaystyle\sum_{j \neq i}{1 \over m}$
= $1 + {(n-1) \over m}$

$m \gg n$ 이라면, $1 + {(n-1) \over m} \approx 1$ 이다. 즉, $m \gg n$ 조건만 지켜진다면 chain의 크기의 기댓값은 $O(1)$ 이다. Chain의 크기가 작다면 $find(k)$ 와 $insert(x), delete(k)$ 동적 연산도 $O(1)$ 시간이 소요된다. 물론, $insert(x), delete(k)$ 동적 연산의 경우 $m \gg n$ 을 유지하기 위해 가끔씩 direct access array의 크기를 수정하여 다시 생성한 후 hash function을 다시 고르고 hash table에 다시 원소들을 넣어줘야 할 수도 있다. 따라서, $insert(x), delete(k)$ 동적 연산의 경우 2.Data Structures에서 배웠던 $O(1)$ amortization bound를 가진다.

정리

Set interface의 $find(k), insert(x), delete(k)$ 연산들을 어떤 자료구조가 효율적으로 도입하는지에 대한 고민을 조금 더 해보는 주제였다. 3. Sorting에서 배웠던 sorted array가 $find(k)$ 연산에 $O(logn)$ , $insert(x), delete(k)$ 에 $O(n)$ 시간이 걸렸었다.

direct access array와 hash table data structure가 위 세가지 연산을 더 $O(1)$ 시간으로 단축시켰다. 추가적으로 direct access array보다 hash table이 메모리 공간을 더 효율적으로 사용한다는 것을 알 수 있었다.

종류	operation	Array $O()$	Sorted Array $O()$	Direct Access Array $O()$	Hash Table $O()$
container	build(X)	$O(n)$	$O(nlogn)$	$O(u)$	$O(n_{(e)})$
static	find(k)	$O(n)$	$O(logn)$	$O(1)$	$O(1_{(e)})$
dynamic	insert(x)/delete(x)	$O(n)$	$O(n)$	$O(1)$	$O(1_{(a)(e)})$
order	find_min()/find_max()	$O(n)$	$O(1)$	$O(u)$	$O(n)$
	find_next(k)/find_prev(k)	$O(n)$	$O(logn)$	$O(u)$	$O(n)$

class Hash_Table_Set:
	def __init__(self, r = 200):
    	self.chain_set = Set_from_Seq(Linked_List_Seq)
        self.A = []
        self.size = 0
        self.r = r
        self.p = 2**31 - 1
        self.a = randing(1, self.p - 1)
        self._compute_bounds()
        self._resize(0)
        
    def __len__(self):
    	return self.size
    def __iter__(self):
    	for X in self.A:
        	yield from X
            
    def build(self, X):
    	for x in X:
        	self.insert(x)
            
    def _hash(self, k, m):
    	return ((self.a * k) % self.p) % m
        
    def _compute_bounds(self):
    	self.upper = len(self.A)
        self.lower = len(self.A) * 100 * 100 // (self.r*self.r)
        
    def _resize(self, n):
    	if (self.lower >= n) or (n >= self.upper):
        	f = self.r // 100
            if self.r % 100:
            	f += 1
            # f = ceil(r / 100)
            m = max(n, 1) * f
            A = [self.chain_set() for _ in range(m)]
            for x in self:
            	h = self._hash(x.key, m)
                A[h].insert(x)
            self.A = A
            self._compute_bounds()
            
    def find(self, k):
    	h = self._hash(k, len(self.A))
        return self.A[h].find(k)
        
    def insert(self, x):
    	self._resize(self.size + 1)
        h = self._hash(x.key, len(self.A))
        added = self.A[h].insert(x)
        if added:
        	self.size += 1
        return added
        
    def delete(self, k):
    	assert len(self) > 0
        h = self._hash(k, len(self.A))
        x = self.A[h].delete(k)
        self.size -= 1
        self._resize(self.size)
        return x
        
    def find_min(self):
    	out = None
        for x in self:
        	if (out is None) or (x.key < out.key):
            	out = x
        return out
        
    def find_max(self):
    	out = None
        for x in self:
        	if (out is None) or (x.key > out.key):
            	out = x
        return out
        
    def find_next(self, k):
    	out = None
        for x in self:
        	if x.key > k:
            	if (out is None) or (x.key < out.key):
                	out = x
        return out
        
    def find_prev(self, k):
    	out = None
        for x in self:
        	if x.key < k:
            	if ( out is None) or (x.key > out.key):
                	out = x
        return out
        
    def iter_order(self):
    	x = self.find_min()
        while x:
        	yield x
            x = self.find_nex(x.key)