MIT 6.006 Introduction to Algorithms 7강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=yndgIDO0zQQ&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=7

7강에서 다룰 interface와 data structure/algorithm

• interface: set
• data structure/algorithm: direct access array sort, counting sort, tuple sort, radix sort

4. Hashing에선 $find(k)$연산을 comparison model에선 $O(logn)$보다 빠르게 수행하지 못하는 한계를 극복하기 위해 direct access array와 hash table을 제시하였다. 비교가 아닌 key에 따라 메모리 공간 상의 위치를 배치함으로써 $find(k)$ 연산에 $O(1)$시간이 걸리도록 최적화하였다.

이번 단원에선 3. Sorting에서 다뤘던 comparison model에서 $build(X)$를 $O(nlogn)$에 연산하는 것이 최선이었음을 증명한다. 그 후, direct access array에 착안하여 $O(n+u)$혹은 $O(n+nlog_n(u))$시간이 걸리도록 $build(X)$를 연산하는 새로운 방법을 제시한다.

Comparison Sorting

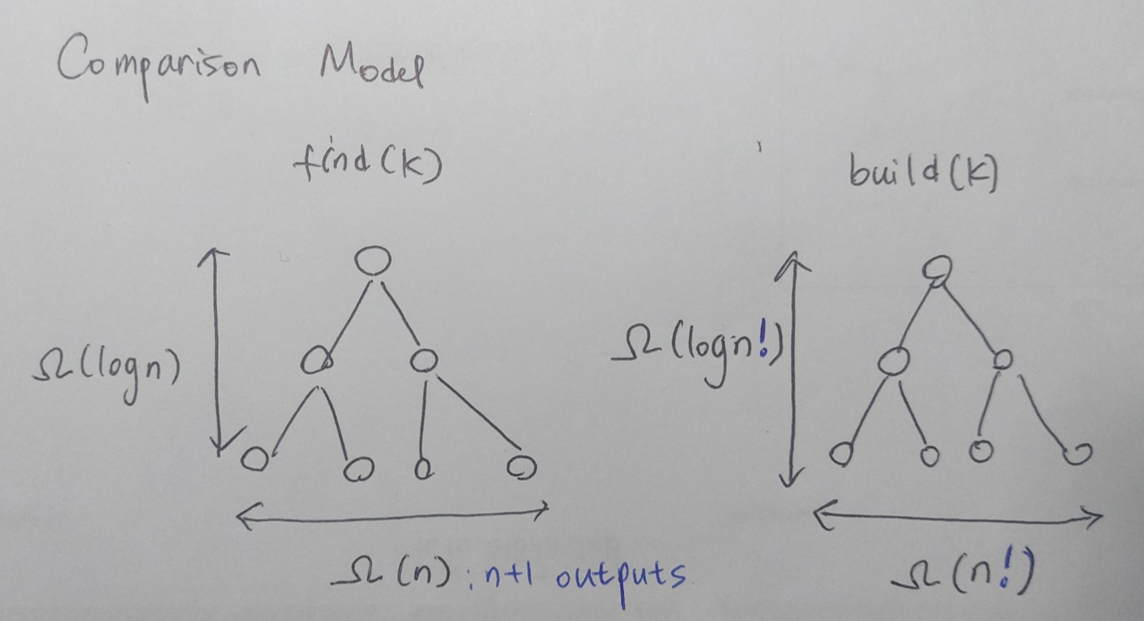
4. Hashing comparison model에서는 $find(k)$를 $\Omega(logn)$보다 빠르게 연산을 수행할 수 없음을 증명했다. 이번에는 $build(X)$에 최소 $\Omega(nlogn)$ 시간이 걸림을 증명해보자. $|A| = n$이라고 할 때 array의 가능한 정렬 가짓수는 $n!$이다. 따라서, $find(k)$의 leaves가 최소 $n+1$개인 binary tree의 높이가 $\Omega(logn)$였던 것처럼, $build(X)$의 leaves가 최소 $n!$개인 binary tree의 높이는 $\Omega(logn!)$이다.

N과 n!이 왜 나왔는지 다시 쉽게 풀어쓰면, $find(k)$는 n개의 원소 중 k 하나를 찾는 연산이다. $build(X)$는 정렬 가능한 n!가지 경우의 수 중 오름차순으로 정렬이 된 한 가지 경우를 찾는 연산이다.

• array의 정렬 가짓수
  $[n(n-1)...1] \geq [n(n-1)...{n\over2}]\geq{n\over2}^{n\over2}$
  $log(n!)\geq log({n\over2}^{n\over2})={n\over2}log({n\over2})=O(nlogn)$

위의 증명에 따라 $build(X)$에 $\Omega(logn!)$, 즉 $O(nlogn)$이 소요된다.

Direct Access Array Sort

$build(X)$를 $O(nlogn)$보다 더 빠른 속도로 연산하기 위해 comparison model의 틀에서 벗어나야 한다. $find(x)$의 시간을 단축했었던 방법을 회상해보면 comparison model의 핵심 개념인 branching factor를 선형적으로 늘림으로써 decision tree의 높이를 $O(1)$로 줄였었다. 다시 말하면, decision tree의 높이를 줄이기 위해 넓이를 늘린 셈이다. 이러한 사고의 전환이 돌파구를 마련했는데 $build(X)$에도 이러한 해결방법을 적용해볼 수 있다.

Direct access array의 아이디어를 sorting에 적용하기 전, 개념을 단순화하기 위하여 두 가지 가정을 한다.

P1 & P2

• P1. key는 중복되지 않는다.
  이유: collision이 없는 상황을 가정하기 위함
• P2. key가 $n \leq u$, $\{0, ..., u-1\}$의 한정된 범위에 국한된다. 이 때, $u$가 충분히 작다.
  이유: direct access array 자체를 생성할 때 $O(u)$ 시간이 걸리는데 $u$가 너무 크다면, $O(nlogn) \leq O(u)$이 되고, $build(X)$ 연산을 수행하는 데에 $O(nlogn)$보다 효율적으로 sorting하는 자료구조를 찾고자 하는 취지에 벗어난다.

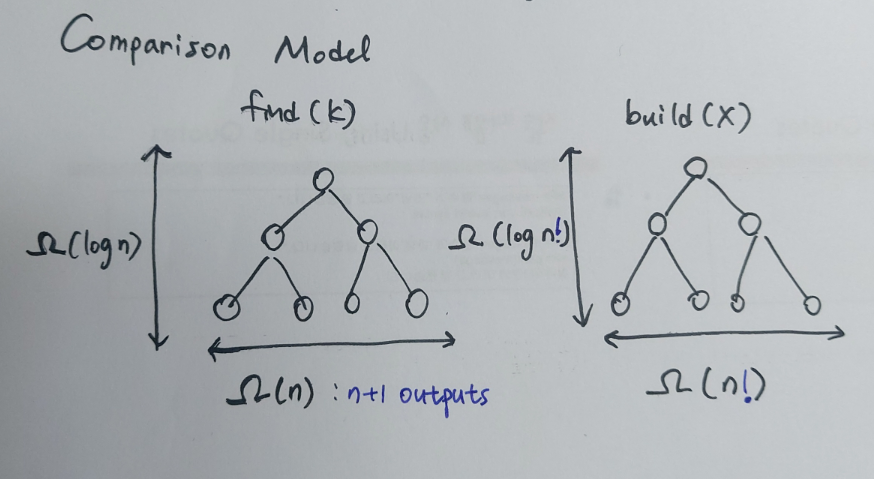
Direct access array sort는 key의 범위에 따라 크게 $u=O(n)$, $u=\Omega(n^2)<n^2$로 나누어서 설명해본다. 잠깐 다시 상기시켜보면, $u$는 $n$의 key 값 중 가장 큰 값이다.

1) $u=O(n)$

$u=O(n)$의 경우, sorting 알고리즘은 크게 3가지 단계로 나뉜다.

1. $u$크기의 direct access array를 만든다. $O(u)$
2. x.key의 위치에 x의 item을 저장한다. $n * O(1)$
3. DAA를 왼쪽에서 오른쪽으로 읽으면서 item이 있다면 값을 반환한다. $O(u)$

1, 2, 3 단계를 합친 연산량이 총 연산량이 된다.
$O(u) + n*O(1) + O(u) \simeq O(n+u)$

$u=O(n)$이기 때문에 $O(n+u) \simeq O(n)$이 된다. 이는 sorted array를 $build(X)$할 때 merge sort가 $O(nlogn)$ 시간이 걸리는 것에 비해 효율적이다.

def direct_access_sort(A):
	" Sort A assuming items have distinct non-negative keys"
    u = 1 + max([x.key for x in A])			# O(n) find maximum key
    D = [None] * u							# O(u) direct access key
    for x in A:								# O(n) insert items
    	D[x.key] = x
    i = 0
    for key in range(u):					# O(u) read out items in order
    	if D[key] is not None:
        	A[i] = D[key]
            i += 1

2) $u=\Omega(n^2)<n^2$

$u=O(n)$에서 key의 범위가 한정되어 있었는데 범위를 조금 더 확장해본다. 소화가 안된다면 쪼개서 흡수해야 하는 것처럼 큰 범위를 해석하기 위해 범위를 작은 조각으로 나누어본다. 여기서는 key $k$를 두 부분으로 쪼개 tuple로 나타내는 방법을 사용한다. 하나의 값을 나머지와 몫으로 나눠서 tuple로 나타내고자 하는데 각 숫자의 의미는 다음과 같다.

$k => (a, b)$

• $k = an + b$
  • $a = k\ //\ n$
  • $b = k\ \%\ n$

참고로, 위와 같은 연산은 파이썬에서 $(a, b) = divmod(k, n)$으로 내장되어 있다.
Divmod 연산을 더 쉽게 이해하기 위해 예를 들어보자. [17, 3, 24, 22, 12] 인 배열이 있다. n=5으로 나누었을 때의 (몫, 나머지) tuple로 배열을 바꿔보면 [(3,2), (0,3), (4,4), (4,2), (2,2)]이 된다. Tuple을 단순화시켜 정수값으로 나타내보면 [32, 03, 44, 42, 22] 이다.

여태 배열의 item을 정렬해보았지만 tuple을 정렬하는 것은 새로운 개념이다. 따라서, 원활한 이해를 위해 별도의 주제로 다룬다.

P1-S: Tuple Sort

Tuple Sort를 이해하기 전에 most significant, least significant라는 개념을 알아야 한다. 튜플 (a, b)에서 a가 더 중요한지 b가 더 중요한지 판단하기 위해선, $pi$를 떠올려본다. 파이를 보통 3.14로 기억하지 3.14159...으로 기억하는 사람은 많지 않다. 뒤에 있는 숫자일 수록 정확도를 높이지만 생략해도 무방하기 때문이다. 즉, 앞에 오는 숫자일수록 중요하고, 뒤에 오는 숫자일수록 중요성이 떨어진다. 이러한 맥락에서 튜플 (a, b)에서 most significant한 숫자는 a, least significant한 숫자는 b가 된다.

이제 (a, b) 중 어떤 위치에 있는 숫자를 먼저 정렬해야하는지 정해야 한다. 주인공은 마지막에 등장한다는 말이 있다. 덜 중요한 숫자부터 정렬한 후, 중요한 숫자를 정렬해야 한다.

정답을 알지만 오답을 통해 더 깊은 이해를 해본다.
우선, 더 중요한 숫자부터 정렬하면 어떻게 되는지 살펴보자.

<예시1> most significant 먼저 정렬

• $O$: [32, 03, 44, 42, 22]
  most significant 정렬
• $A1$: [03, 22, 32, 44, 42]
  least significant 정렬
• $B1$: [22, 32, 42, 03, 44]

most significant으로 정렬된 배열 $A1$을 기준으로 least significant정렬하면 a위치의 순서가 보존되지 않는 것을 확인할 수 있다.

<예시2> least significant 먼저 정렬

• $O$: [32, 03, 44, 42, 22]
  least significant 정렬
• $A2$: [32, 42, 22, 03, 44]
  most significant 정렬
• $B2$: [03, 22, 32, 42, 44]

least significant으로 정렬된 배열 $A2$를 기준으로 most significant정렬했을 때 b위치의 순서가 마찬가지로 보존되지 않는 것을 확인할 수 있다. 하지만 $B1$과 달리 $B2$는 자연스럽다고 느낀다. 마지막 순서에 정렬해야 의미가 보존되는데 앞의 숫자의 의미가 가장 중요하기 때문에 앞의 숫자를 마지막 순서로 정렬해야 한다. 앞에 있는 숫자 a가 작아야 작은 숫자이기 때문이다. 숫자 b는 같은 a 내에서 순서를 정할 때만 의미가 있다. 한 문장으로 요약하면, least significant bit > most significant bit 순서로 정렬해야 한다.

잠시 direct access array sort에서 했던 두 가지 가정을 상기시켜보면 다음과 같다.

1. key는 중복되지 않는다.
2. key가 $n \leq u$, $\{0, ..., u-1\}$의 한정된 범위에 국한된다. 이 때, $u$가 충분히 작다.

Tuple sort는 $u=\Omega(n^2)<n^2$ 범위에서도 direct access array sort가 가능하게함으로써 u가 충분히 작다는 2번 가정으로부터 벗어나게 되었다.

<예시1>, <예시2>에서 $B1, B2$와 같은 두 번째 정렬을 수행할 때, 원래의 $O$ 대신 $A1, A2$을 기준으로 정렬했다. 이는 key값의 순서를 기억한다는 뜻이다. 순서를 기억한다는 것을 stable하다고 표현하며 이는 tuple sort를 제대로 하기 위한 필요조건이다. Stable하게 정렬하기 위해 순서를 기억하게 해주는 기능을 counting sort가 담당한다.

P2-S. Counting Sort

Stable하게 정렬하기 위해, 순서를 기억하게 해주는 기능이 필요한 이유는 배열에 튜플을 저장해야하기 때문이다. 튜플을 저장하게 되면 key값이 한개에서 두개로 늘어난다. 따라서, key는 중복되지 않는다는 1번 가정에 반하는 상황이다.

Key 값의 중복을 collision이라는 용어로 4.Hashing에서 배웠다. 이 때, hash table은 chaining 개념을 도입해서 collision을 해결하였다. 만일 chaining을 정렬에 적용해보면 다음 그림과 같다.

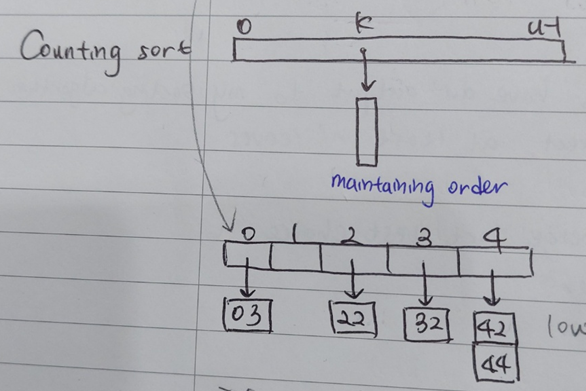
위의 그림에서 먼저 (a,b) 튜플에서 least significant한 bit인 b를 기준으로 direct access array로 정렬한다. 그 다음엔, 정렬된 숫자를 왼쪽에서부터 훑어가면서 most significant한 bit인 a를 기준으로 다른 메모리 공간에 저장한다. 다만, 이때 a가 중복이라면 collision이 일어난다. 여기서 순서를 기억하게 해주는 기능은 chaining의 순서를 통해 구현한다. Chaining될 값은 기준으로 하는 direct access array로부터 오름차순으로 값을 읽어온다. 그렇기 때문에 자연스레 같은 a 내에서는 b 역시 오름차순으로 저장된다.

1. $u$크기의 direct access array를 만든다. $O(u')$
2. x.key의 위치에 x의 item을 저장한다. $n * O(1)$
3. DAA를 왼쪽에서 오른쪽으로 읽으면서 item이 있다면 값을 chain에 저장한다. $O(u')$
4. chain에 저장되어 있는 값을 순서대로 반환한다. $O(n)$

1, 2, 3, 4 단계를 합친 연산량이 총 연산량이 된다.
$O(u') + n*O(1) + O(u') + O(n) \simeq O(n+2u')$

$u=O(n^2)$이지만, modulus로 인해 $u'=O(n)$이기 때문에 $O(n+2u') \simeq O(n)$이 된다. 요약하면 $u=O(n)$ 뿐 아니라 $u=O(n^2)$에서도 sorted array를 $build(X)$할 때 $O(n)$ 시간이 걸린다.

간단한 예시를 통해 다른 관점에서도 생각해보면, $u < n^2$, 즉 $u < 25$일 때 modulus 5로 나눠보면 (a,b) 튜플이 반환된다. 이때, b에 대하여 정렬한 후, a에 대해 정렬한다. 여기서 $0 < a, b < 5$이므로 $O(n+u) = O(n+2n) \simeq O(n)$이 된다.

def counting_sort(A):
	"Sort A assuming items have non-negative keys"
    u = 1 + max([x.key for x in A])		# O(n) find maximum key
    D = [[] for i in range(u)]			# O(u) direct access array of chains
    for x in A:							# O(n) insert into chain at x.key
    	D[x.key].append(x)
    i = 0
    for chain in D:						# O(u) read out items in order
    	for x in chain:
        	A[i] = x
            i += 1

Radix Sort

$u\leq n^2$에서 범위를 $u\leq n^c$으로 확장해본다.

$u\leq n^2$에서 $u$를 2개 인자를 가진 튜플로 표현할 수 있는 것처럼 $u\leq n^c$의 $u$를 c개의 인자를 가진 튜플로 표현할 수 있다. 튜플의 각 인자를 least significant bit부터 most significant bit 순서대로 정렬하면 $O(n+cn)$시간이 소요된다.

$u\leq n^c$
$log_nu\leq c$

이므로 $O(n+cn) = O(n+nlog_nu)$과 같다. 그렇기 때문에 $build(X)$에 radix sort는 $O(n+nlog_nu)$시간이 소요된다. 따라서, u가 너무 크지 않다면 $build(X)$를 merge sort의 $O(nlogn)$보다 더 효율적으로 연산한다.

종류	operation	Insertion Sort	Selection Sort	Merge Sort	Counting Sort	Radix Sort
container	build(X)	$O(n^2)$	$O(n^2)$	$O(nlogn)$	$O(n+u)$	$O(n+nlog_n(u))$

def radix_sort(A):
	"Sort A assuming items have non-negative keys"
    n = len(A)
    u = 1 + max([x.key for x in A])				# O(n) find maximum key
    c = 1 + (u.bit_length() // n.bit_length())
    class Obj: pass
    D = [Obj() for a in A]
    for i in range(n):							# O(nc) make digit tuples
    	D[i].digits = []
        D[i].item = A[i]
        high = A[i].key
        for j in range(c):						# O(c) make digit tuple
        	high, low = divmod(high, n)
            D[i].digits.append(low)
    for i in range(c):							# O(nc) sort each digit
    	for j in range(n):						# O(n) assign key i to tuples
        	D[i].key = D[j].digits[i]
        counting_sort(D)
    for i in range(n):							# O(n) assign key i to tuples
    	A[i] = D[i].item						# O(n) output to A