스탠포드 강의의 CS231n 5강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=bNb2fEVKeEo&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=5

1. 이미지 classification을 위한 neural network 조건

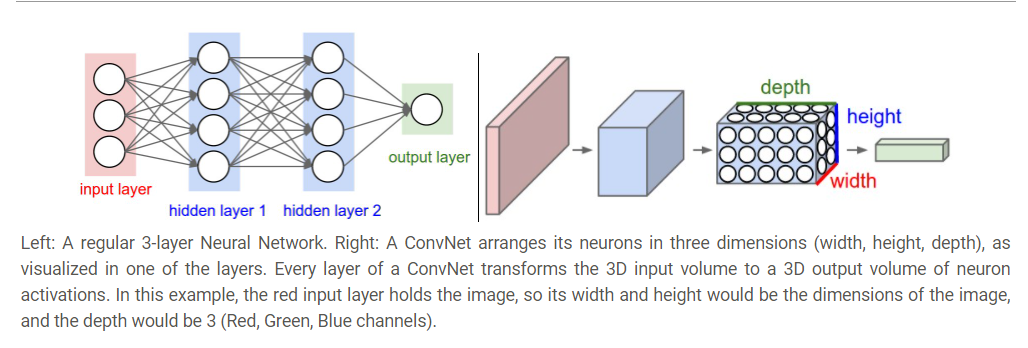
4강에선 hidden layer와 output layer 모두가 fully connected된 기본적인 형태의 neural network가 소개되었다. 기본적인 형태에서 더 나아가, 2강에서 언급된 image classification task에 적합한 neural network란 무엇일까? Activation function에 통과시킨 fully connected layer를 단순히 깊게 쌓아주면 되는 것일까? 두 가지 대표적인 이유로 fully connected layer로만 이루어진 neural network는 image classification에 적합하지 않다.

조건 1: 공간적 정보 보존

첫째, hidden layer와 output layer 모두가 fully connected layer로 이루어져 있다면 이미지의 공간적 정보가 손실된다. 사진을 인식할 땐 공간적인 특성을 파악하는 것이 중요하다. 그런데 fully connected layer로만 이루어진 신경망은 1차원 vector만을 입력으로 받는다. 그렇기 때문에 3차원 이미지 정보를 reshape를 통해 1차원 vector로 펴서 입력을 해줘야하는데 그 과정에서 공간적 정보가 손실된다. 공간적 정보를 보존하기 위해 바꿔줘야 할 것은

공간적 정보 보존
1. 공간적인 정보를 보존한 채, 학습을 하기 위해 3차원 이미지 정보(width, height, depth)를 그대로 입력받아야 한다.

• 참고 : width와 height 뿐 아니라, rgb 색상까지 입력받으면 depth라는 차원이 추가되어서 3차원 정보이다.

2. 입력받은 3차원 이미지를 학습하기 위해 weight 역시 3차원으로 바뀌어야 할 것이다.

2번 문제를 해결하기 위해 만들어진 3차원 weight가 바로 filter라는 개념이다. 3차원 filter를 통해 입력된 이미지의 픽셀에 slide하면서 weight(filter)와 입력 이미지를 dot product하게된다. 이를 통해 weight와 입력 이미지 간의 관계를 알 수 있다.

Convolution 연산은 두 함수 중 하나를 반전시킨 후 t만큼 이동시켜 [-∞,∞] 범위에서 inner product를 계산한다. 물론 이미지와 filter의 내적은 반전이라는 개념이 빠졌지만 두 개의 함수를 '전범위'에 대해 'dot product'한다는 점이 비슷해서 이러한 filter를 convolutional filter라고 하고, 이러한 원리를 쓰는 layer들을 convolutional layer라고 한다. 한마디로 convolution이란 뉴런의 activation을 최대화시켜주는 input이 무엇인지 파악한다. 파악 후, filter와 이미지 간의 correlation을 최대화한다.

물론 각 class의 score를 구한 후 classification을 하기 위해 마지막 layer 들은 기존의 fully connected layer를 사용하나, 입력에서부터 fully connected layer 전까지 convolutional layer를 쓰도록 하는 neural network이 바로 convolutional neural network다.

조건 2: Parameter 수 조절

이미지는 width, height, depth라는 3차원 벡터로 입력되는데 이 모든 정보를 다음 layer의 모든 뉴런에 연결시켜주게된다면 parameter 수가 너무 많아지게 된다.

Parameter 수가 많아지면 학습이 느려지고 비효율적이다

• 문제 : Fully connected layer로 입력 정보, 예를 들어 (200, 200, 3) 정보를 입력해주고 10개의 뉴런이 있는 다음 layer에 모두 연결시켜주게 된다면 한 layer에서 학습해야 할 parameter 수는 200x200x3x10=1,200,000이 된다. 그렇게 되면 layer가 깊어질수록 학습해야 할 parameter 수가 너무 많아지게 된다.

이 문제를 해결하기 위해 fully connected layer로 모든 입력 정보를 다음 layer의 모든 뉴런과 연결시키는 대신에 local한 정보만을 연결하는 방법을 생각해볼 수 있다. Local한 정보만을 본다는 것은 입력 정보, 혹은 직전 layer의 모든 부분을 연결시키는 대신 local한 부분만을 연결시키게 된다는 것이다. 밑의 그림을 보면 1개의 뉴런이 보는 영역이 이미지 전체가 아닌 일부라는 것을 알 수 있다.

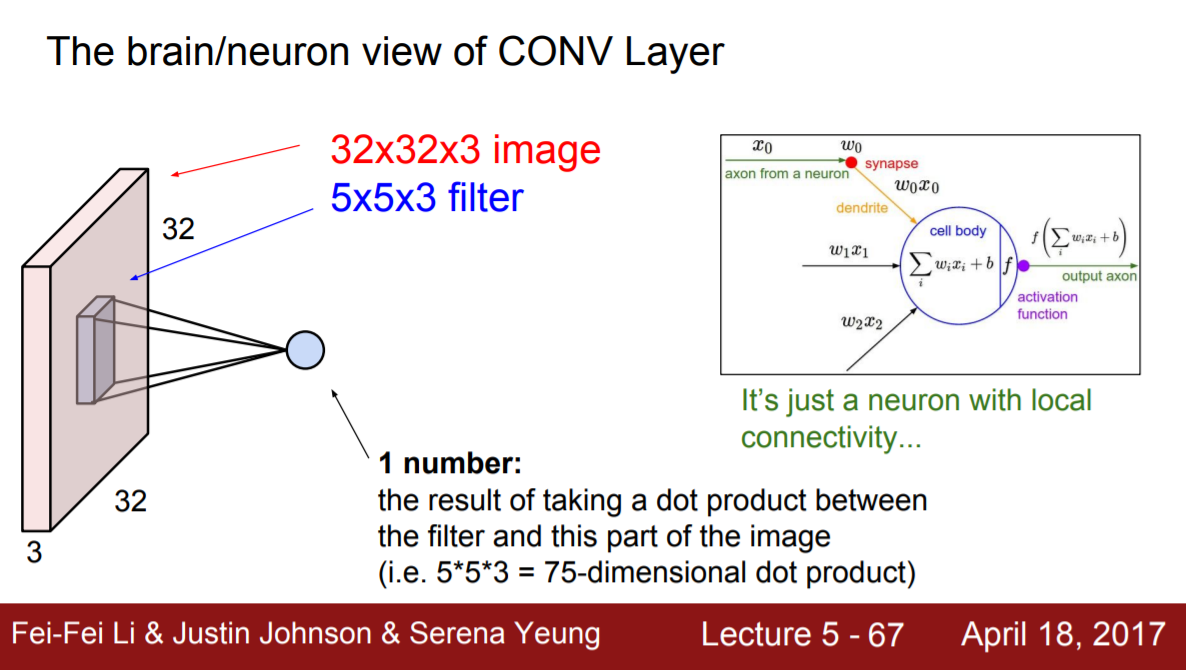
이미지의 local한 부분의 크기를 결정해주는 것이 filter의 크기다. 여기서 주의할 점은 filter가 2차원 영역(width, height)에 대해 local하지만 depth에 대해서는 full connectivity를 유지한다는 것이다. (직관적으로도 와닿는게 depth가 r,g,b색상이라고 할 때, 일부 색상에 대해서만 본다면 학습이 제대로 이루어지지 않을 것 같다.) Full connectivity를 유지한다는 것은 입력된 이미지 혹은 전 convolutional layer의 depth와 filter의 depth가 일치한다는 뜻이다.
앞서, image의 depth와 filter의 depth는 동일해야 한다고 했는데 그렇다면 depth는 ConvNet 전체에서 동일하게 유지되는걸까? 아니다. Convolutional layer의 depth는 전 layer의 depth가 아닌 filter의 개수와 동일하다.

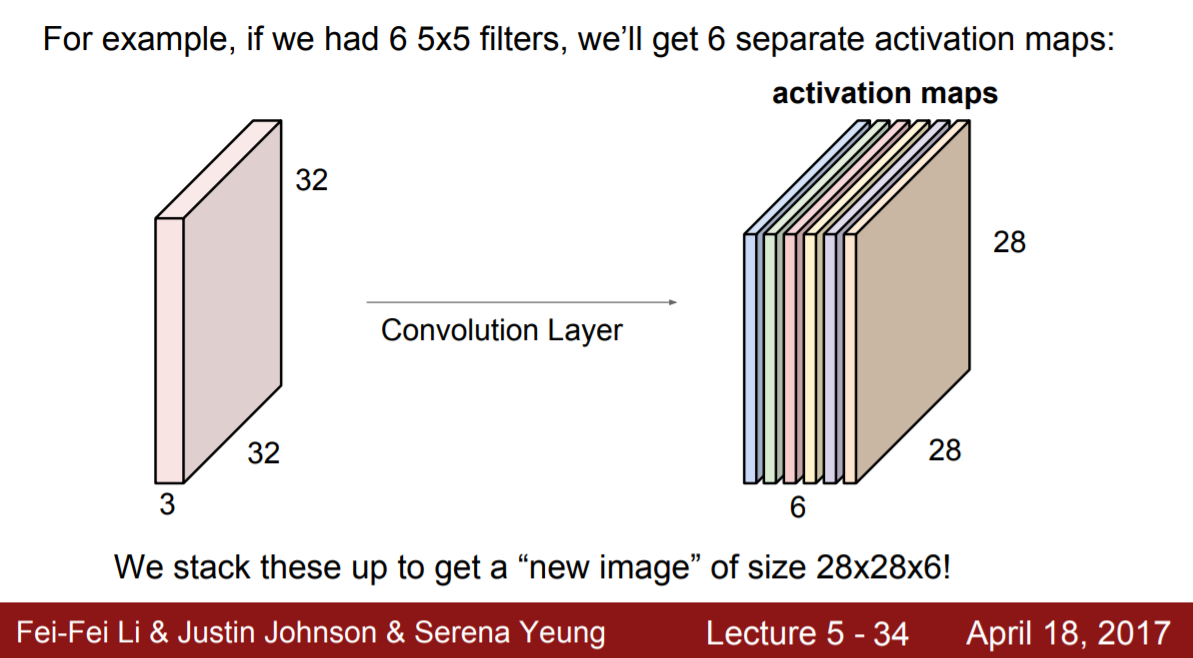
왜 그렇게 될까? 우선, convolutional layer의 weight인 filter를 공유하는 뉴런들의 집합이 바로 activation map이다. 여기서 filter는 특징을 나타내므로 filter를 공유한다는 것은 특징을 공유한다는 뜻이다. 즉, weight matrix를 공유하기 때문에 하나의 filter에 대해 학습된 특징을 위치에 상관없이 인식하게 되는 효과가 있다. 다시 말해서, local한 특징에 대해 전체 위치에서 살펴볼 수 있다는 것이다.

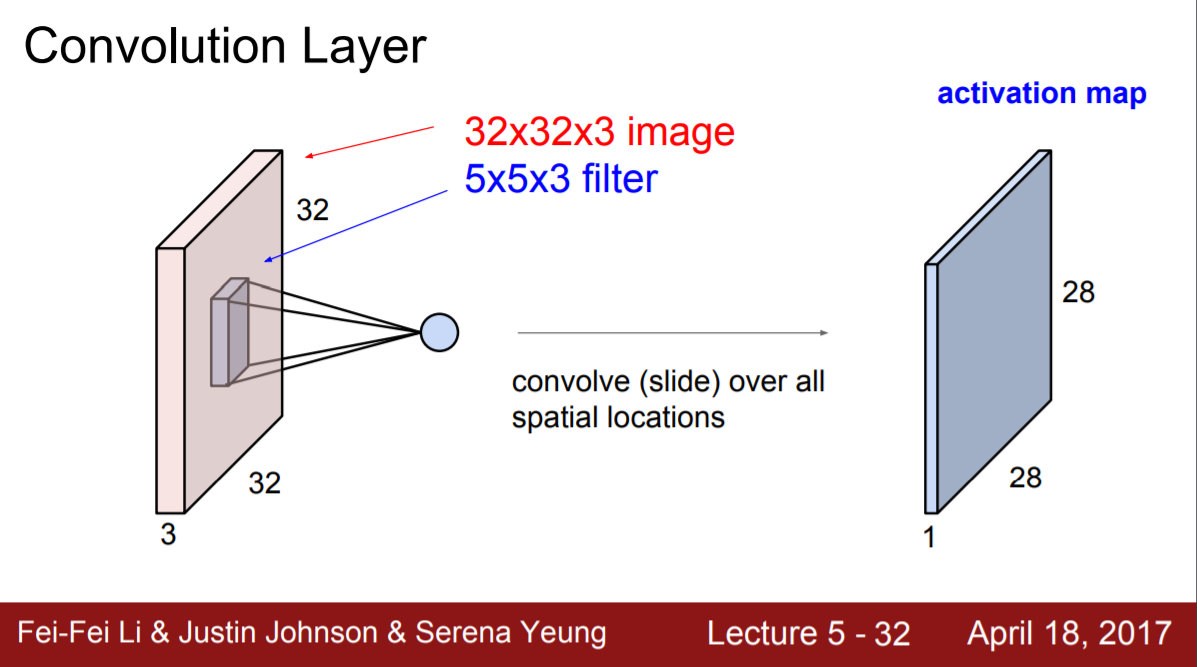
Neural network의 경우에는 앞 강의에서 언급했던 차의 비유에서 여러 색깔의 차 중에서 weight를 학습하므로 다양한 색깔의 차를 제대로 분류할 수 있게 된다는 것을 상기시켜보자. Convolutional neural network 역시 neural network이기 때문에 여러가지 특징을 토대로 학습을 한다. 그러기 위한 방법으로 filter를 여러 개 사용한다. 아래의 그림에선 5개의 filter를 사용해서 다음 convolutional layer의 depth는 5가 된다. 이 때, 각 filter는 다른 특징을 나타내기 때문에 값은 다르겠지만, 두 개의 convolutional layer 사이의 filter 크기는 차원을 맞춰주기 위해 통일시키므로 아래 그림에서 5개의 뉴런은 같은 receptive field를 가진다.

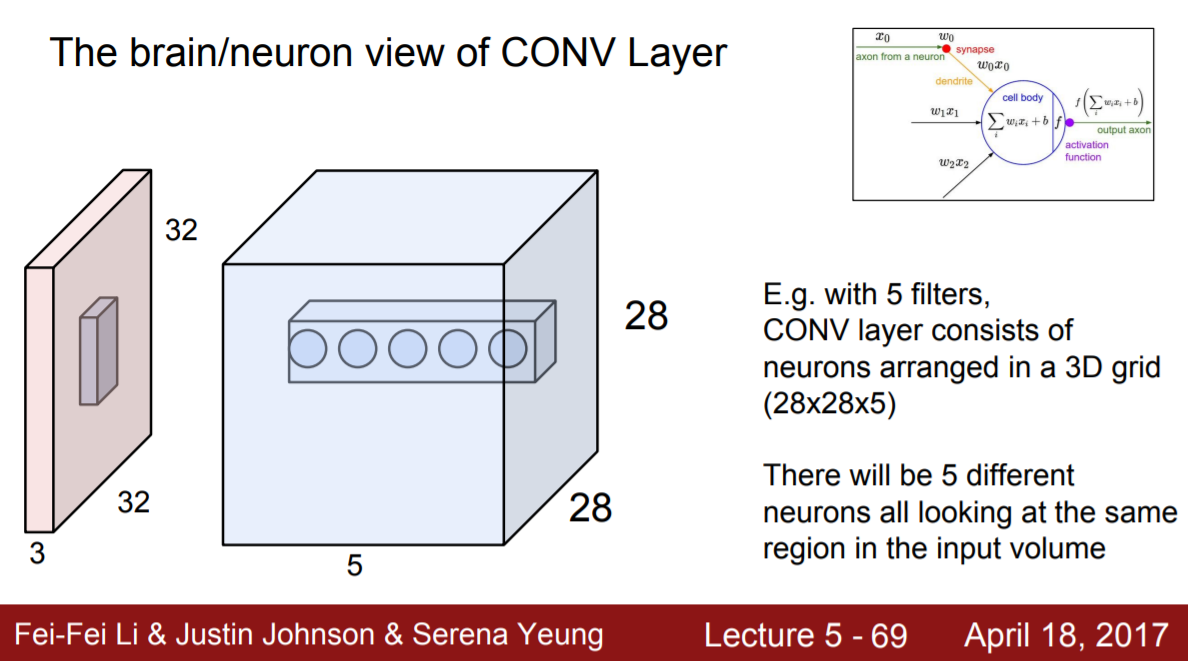
2번째 조건에서 filter의 개념을 다른 측면에서도 이해해봤다.

이쯤되어서 드는 의문이, 만약 local한 영역만 뉴런에 연결시켜준다면, 나무에만 집중하게되어 숲을 못 보는 것은 아닐까? 여기서 나오는 개념이 receptive field라는 hyperparameter이다.

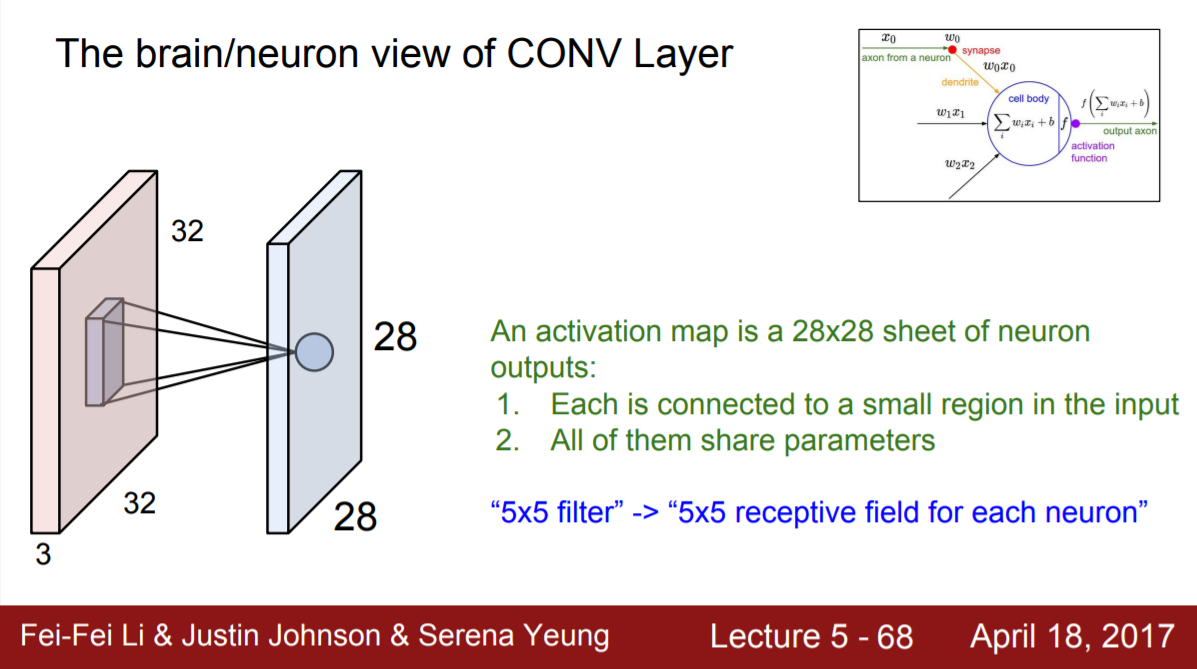
위의 그림에서와 같이 하나의 filter를 통과시킨 activation map(layer)의 뉴런이 볼 수 있는 영역(receptive field)은 filter의 크기와 동일하다. 하지만 neural network를 깊게 쌓아줄수록 receptive field는 넓어진다. 아래 그림에서 볼 수 있듯이

• layer2에서 한칸(초록색 영역)이 볼 수 있는 layer1의 receptive field는 3x3인데
• layer3에서 한칸(노란색 영역)이 볼 수 있는 layer1의 receptive field는 5x5이다.

즉, 신경망이 깊어질수록 하나의 뉴런이 볼 수 있는 receptive field가 넓어지는 것을 시각적으로도 확인해봤다.

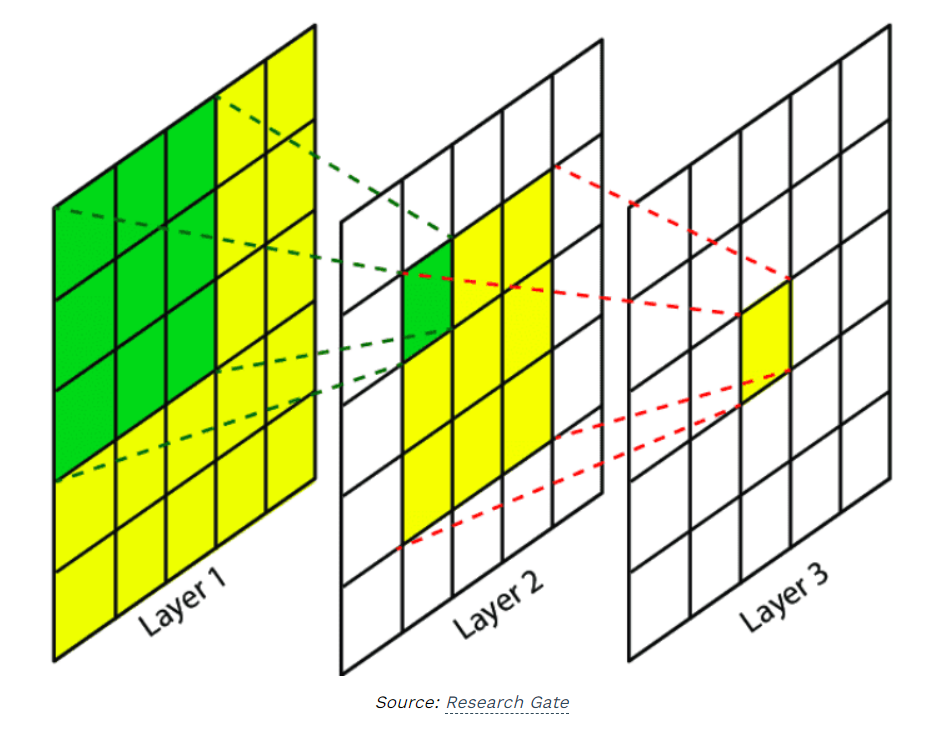
추가적으로, 신경망이 깊어질수록 receptive field가 커진다는 것의 의미를 생각해보자. 초반의 layer들에서는 간단하고 구체적인 특징들을 학습하게되지만 많은 layer들을 쌓아주면서 receptive field가 커지면서 더 복잡하고 추상적인 특징들을 볼 수 있게된다.

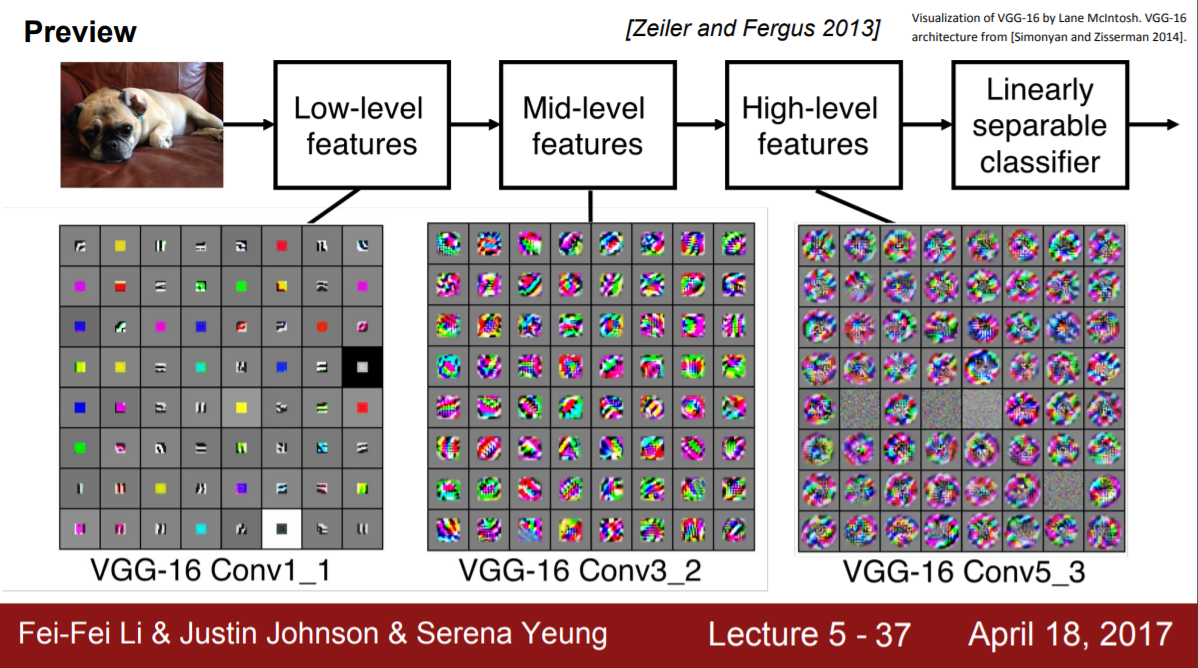
2. ConvNet Architecture - 1

Layers

먼저, ConvNet의 전체적인 구조를 시각화하면 아래의 그림과 같다.

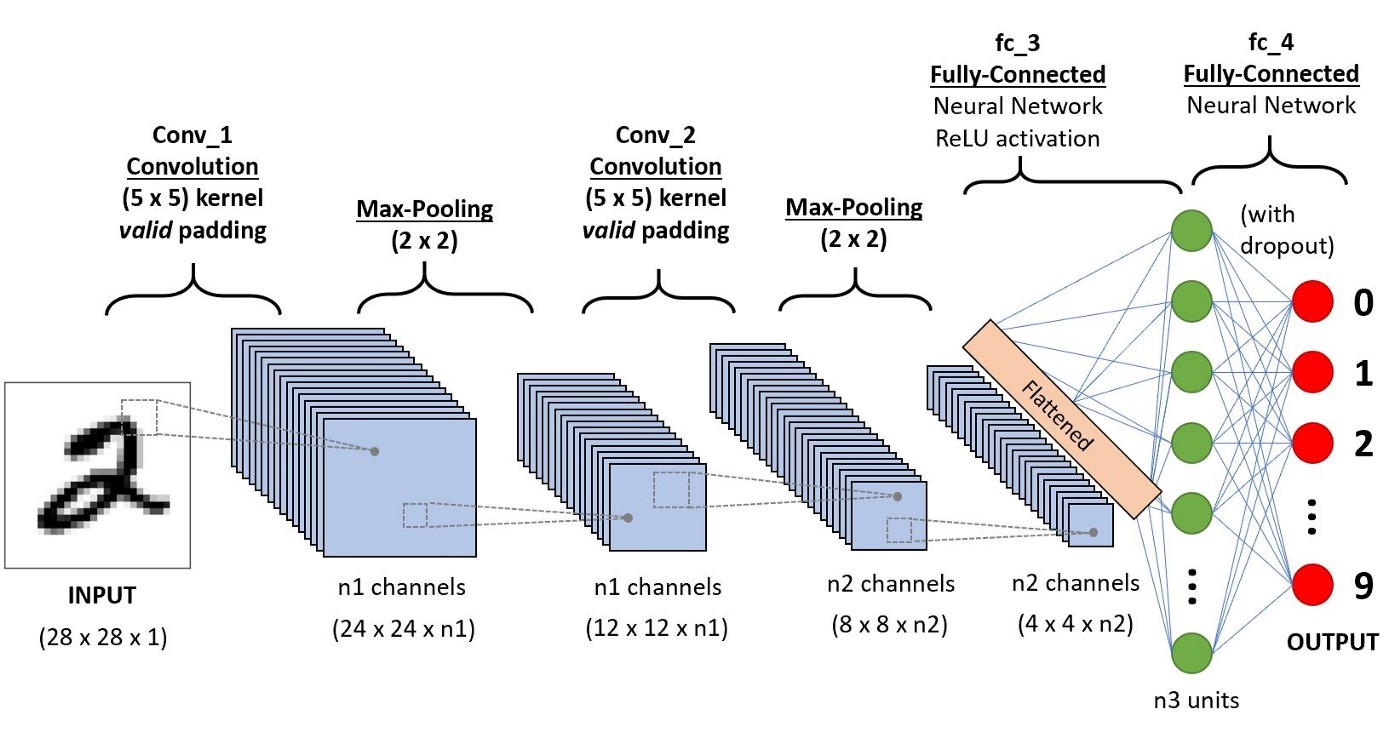
Convolutional Neural network의 전체적인 구조를 이제 정리해보자.

• Input - convolutional layer - batch normalization - relu activation - pooling layer - fully connected layer

앞서 가장 기본적인 형태의 neural network가 아닌 convolutional neural network의 경우 fully connected layer 앞에 convolutional layers를 추가해준다고 했었다. 이제 그 사이에 들어가는 pooling layer라는 개념도 배울 것이다. 물론 ConvNet에서 activation이나 batch normalization도 적용하지만 6강에서 자세히 알아가고, ConvNet의 가장 기본적인 틀을 이루는 Convolutional layer, pooling layer, fully connected layer 세 부분을 중점으로 보자.

Tradeoff(parameter 수 vs deep neural network)

단순히 개념들을 나열하기보다는 ConvNet이 neural network로서 가지는 특성을 중심으로 살펴보겠다. Neural network를 왜 깊게 쌓아주는지를 상기시켜보자. 비선형적인 단순한 특징들로부터 추상적인 특징들까지 학습하기 위함이다. 이때 핵심은 가능한 적은 parameter로 신경망을 깊게 쌓아주는 것이 목표였다. 하지만 신경망을 깊게 쌓아주려면 parameter의 수가 늘어나므로 둘은 tradeoff 관계에 있다. Tradeoff 관계에 있는 두 가지 특성이 있을 땐 그 정도를 상황에 따라 적절히 조절하는 것이 엔지니어의 목표이다. Parameter 수를 줄이기 위해 layer를 거듭할 수록 이미지 크기를 줄이는 downsampling이 요구된다. 그런데 출력 이미지가 layer를 거듭할 수록 너무 급격한 속도로 줄어들게된다면 신경망을 깊게 쌓아주는 것이 불가능해질 것이다. 따라서 dimension 유지를 통해 parameter 수를 줄이진 못해도 신경망을 깊게 쌓을 수 있도록한다. 결국 이 둘의 완급 조절을 하는 것이 모델을 설계하는 엔지니어의 몫이다. 이 두 가지 키워드 downsampling과 dimension 유지 위주로 3가지 종류의 layer를 보자.

• downsampling : parameter 수 감소, neural network의 깊이 줄어듦
• dimension 유지 : parameter 수 증가, neural network의 깊이 늘림

2-1. Convolutional layer

2-1.1 depth

Depth가 filter의 개수라는 점과 filter의 의미에 대해서는 앞 부분에서 설명했으므로 생략한다.

2-1.2 stride(1 : dimension 유지, 2이상 : downsampling)

Filter가 입력 이미지에 대해서 sliding한다고 했었는데 구체적으로 어떻게 움직이는지에 대해서는 설명하지 않았었다. Stride는 필터가 한번에 움직이는 간격이다. 그림으로 먼저 이해해보자.

• stride = 1
  
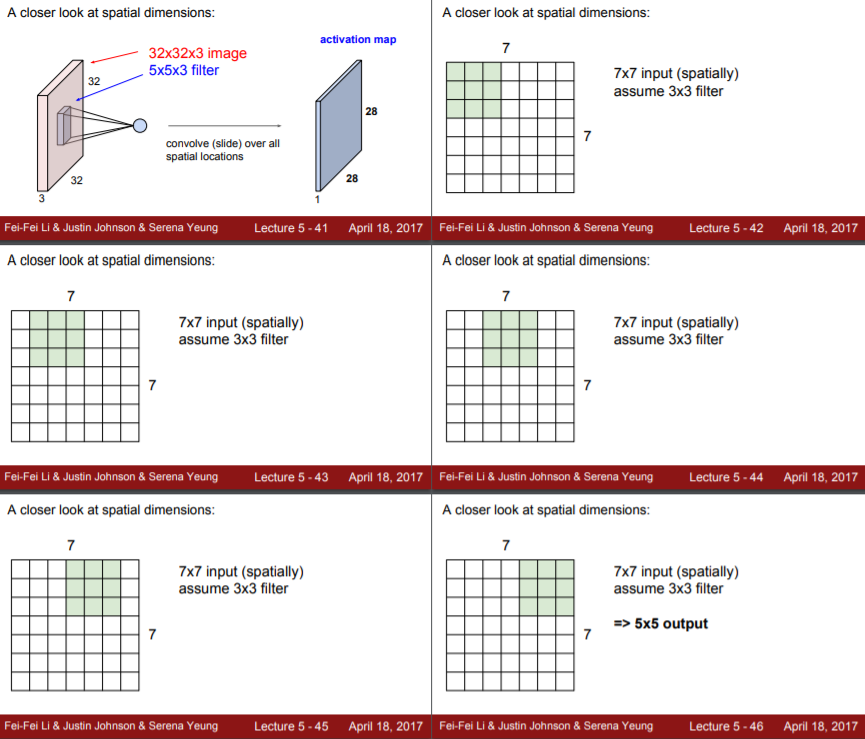
• stride = 2
  
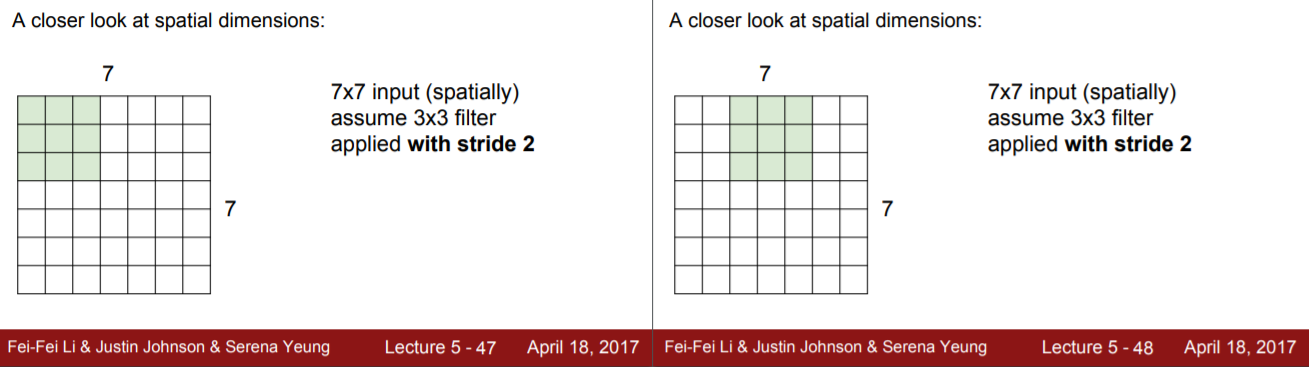
• stride = 3?
  

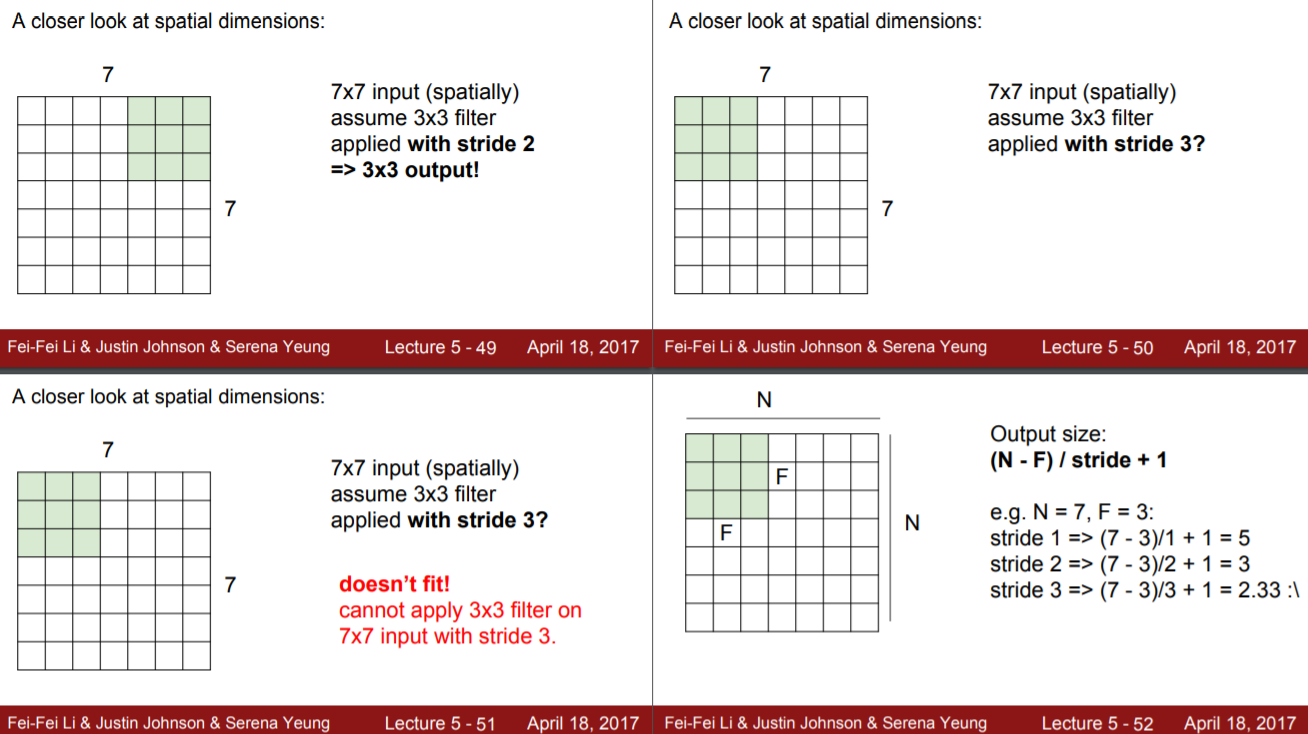
Filter의 stride로 인해 출력되는 이미지의 크기가 줄어드는지(downsampling) 줄어들지 않는지(dimension 유지)를 파악하기 위해 stride에 따라 변하는 이미지의 크기를 공식화하자.

1은 첫번째 좌측 상단에 있는 filter고 N-F만큼 이동하는데 stride가 한번에 이동하는 보폭이므로 (N-F)/stride만큼 개수가 더해진다.

dimension 유지
Stride를 1로 설정하는 경우는 보통 입력 이미지와 출력 이미지의 크기를 같게 유지하고 싶을 때이다. 그런데 위의 예시에서 보면 N=7, F=3일 때, 입력 이미지가 7x7일 때 출력 이미지가 5x5로 크기가 유지가 안된다. 그렇다면 입력 이미지의 크기를 어떻게 해야 보존시킬 수 있을까? 여기서 나오는 개념이 zero padding이다.

downsampling
Stride를 2이상으로 설정하는 경우는 downsampling을 하고 싶을 때이다. 그런데 이 경우에도 zero padding이 필요한 경우가 있다. N=7, F=3, stride=3일 경우 한 번 이동하게 되면 N이 한칸 남게되어서 맞아떨어지지 않는다. 이런 경우에도 zero padding을 통해 N의 크기를 늘려 맞아떨어질 수 있도록 한다.

• 정리
  • stride = 1 : dimension 유지
  • stride >= 2 : downsampling

2-1.3 zero-padding (dimension 유지, downsampling하는 경우도 사용할 때 있음)

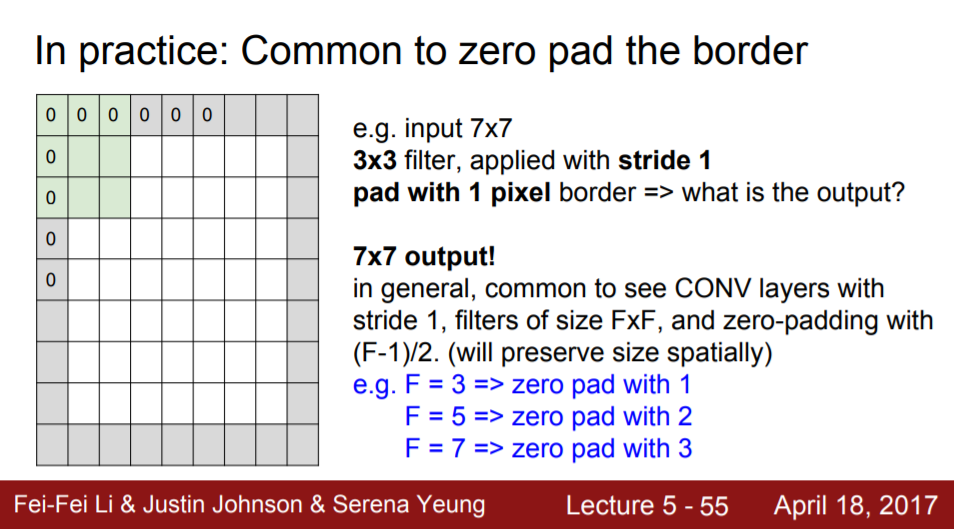
dimension 유지
Stride가 1이고 N=7, F=3일 때 pad=1이라면 N 양쪽으로 pad만큼 붙여주므로 (N-F+2xP)/stride + 1 =(7-3+2x1)+1= 7으로 이미지의 크기가 유지된다. Zero padding은 주로 이런 경우에 사용된다.

downsampling
Stride가 2 이상일 때 위에 그림을 보면 N=7, F=3, stride=3인 경우 pad=1이되면 (N-F+2xP)/stride + 1 = (7-3+2x1)/3 + 1 = 3이 된다. 이처럼 downsampling하는 경우에도 입력된 이미지 전체를 sliding하기 위해 zero padding을 사용할 때도 있다.

참고로 zero padding은 대칭을 유지하기 위해 양쪽 끝에 같은 수의 pad가 붙는다.

zero padding의 의미
차원 측면에서의 유용성 뿐만 아니라 zero padding은 구석 모서리의 정보를 보는 데에도 기여한다. 중요한 특징이 꼭 이미지의 중앙에 위치한다는 보장은 없다. 하지만, padding이 없다면 convolution 필터가 훑는 횟수가 위치에 따라 불균등해지게 된다. 모서리의 정보는 한번, 중앙의 정보는 여러 번 훑게 되기 때문이다. 이 때 zero padding을 통해 모서리의 정보도 내곽에 있는 정보처럼 취급하게 되면 모서리의 정보도 여러 번 훑는 것이 가능해진다. 이로써 위치에 따른 정보의 불균등을 완화해주었다.

2-2. Pooling layer(downsampling)

Pooling layer는 pooling filter를 이용해서 이미지의 크기를 줄일 때 사용한다. Average pooling 등 많은 종류가 있지만 maxpooling의 성능이 좋아서 자주 사용하므로 maxpooling을 설명하겠다.

2-2.1 Maxpooling

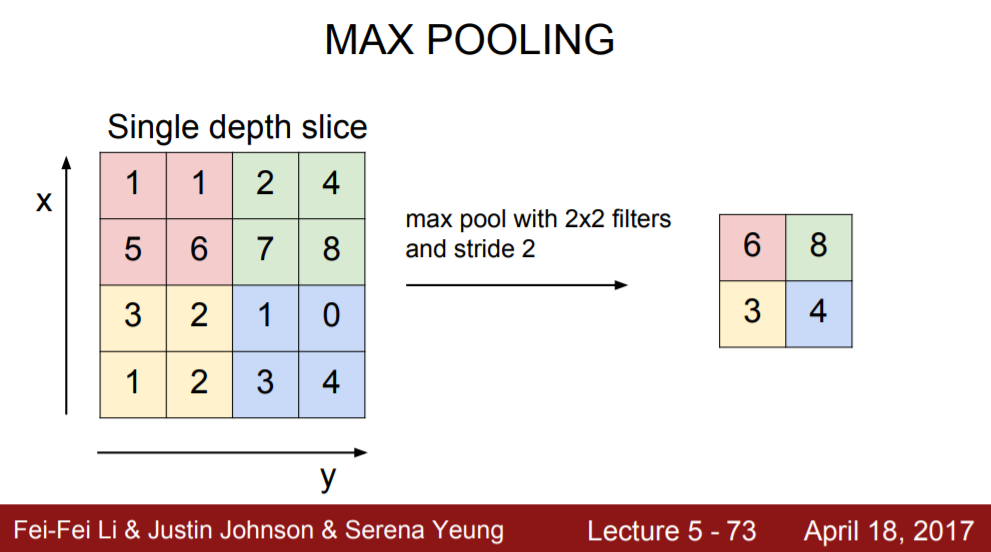
Maxpooling은 위의 그림과 같이 최댓값을 사용한다. Downsampling을 한다는 것은 어떻게 보면 정보를 잃는 것인데 maxpooling은 가장 눈에 띄는 특징을 사용하기 때문에 가장 뚜렷한 정보들을 남기고 나머지 정보들을 잃는 것이다. 그래서 성능이 가장 좋을거라고 예측해본다.

Filter가 겹치지 않도록 하기 위해 pooling 연산을 할 때 filter의 크기만큼 sliding을 한다. 가장 많이 쓰이는 filter는 2x2 filter이므로 2 sliding을 해서 출력 이미지의 크기는 입력 이미지의 절반이 된다.

2-2.2 Convolutional layer stride=2와 2x2 pooling layer 차이?

Convolutional layer의 stride를 2이상으로 잡는 것과 pooling filter를 쓰는 것은 모두 downsampling 기능을 수행하는데 둘이 어떻게 다를까? 둘의 차이는 학습 가능한 parameter의 존재 여부에 있다.

Convolutional layer를 이용하게 되면 학습 가능한 parameter를 사용하게되므로 학습 가능하게 downsampling을 할 수 있다는 장점이 있다. 하지만 parameter가 늘어나므로 학습 연산량이 늘어나는 단점이 있다.

Pooling을 이용하게 되면 학습해야하는 별도의 parameter 없이 pooling filter의 크기라는 hyperparameter 설정만으로 downsampling을 하게된다. 따라서 학습 연상량이 준다는 장점이 있으나, 학습 불가능한 방식으로 downsampling을 수행하므로 convolutional layer의 stride >= 2로 설정하는 것보다 성능이 다소 떨어진다.

최근에는 하드웨어의 성능도 좋아지고 모델이 계속 진화하면서 성능이 중시되면서 pooling layer를 사용하지 않고 convolutional layer의 stride를 늘리는 방식이 많이 사용된다고 한다.

2-3. Fully connected Layer

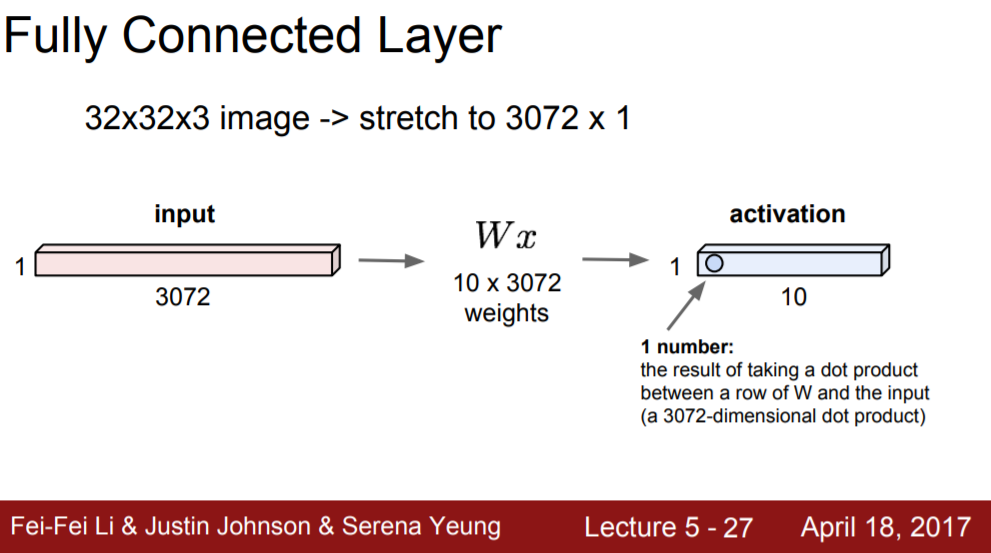
각 class의 score를 구한 후 classification을 하기 위해 convolutional layer들을 통해 neural network를 가능한 적은 parameter로 신경망을 깊게 쌓아준다. Layer를 거듭하면서 작아진 3차원 정보를 flattening을 통해 1차원으로 reshape해준다. 그 후 4강의 마지막 부분에서 배웠던 fully connected layer에 1차원 벡터 값을 연결해준다. 정리하면, convolutional layer와 pooling layer에서 충분히 parameter 수를 줄이고 공간적인 정보를 학습해준 후 비로소 fully connected layer에 연결시킨다.