[MIT 6.006] 6. Binary Trees, Part 1 ( 이진트리, 파트 1 )

Aacara·2023년 4월 18일

자료구조

자료구조 및 알고리즘

목록 보기

6/13

MIT 6.006 Introduction to Algorithms 9강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=76dhtgZt38A&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=9

9강에서 다룰 interface와 data structure

interface: (sequence), set

data structure: binary tree

여태 배운 것 정리

Sequence에서 inserte/delete_first/last를 각각 잘하는 자료구조가 존재했다. insert/delete_first의 경우 linked list가 $O(1)$ 시간이 걸리고, insert/delete_last의 경우 dynamic array가 $O(1_{(a)})$ 시간이 걸린다. 이처럼 특정 위치에 특화된 dynamic 연산을 수행하는 자료구조는 있었지만 insert/delete를 임의의 장소에 효율적으로 수행하는 자료구조는 아직 없었다. 그 이유는 linked list의 경우 array의 중간에 가는 것 자체가 $O(n)$ 시간이 걸리고 dynamic array의 경우 array의 중간을 index를 통해 한번에 도달하지만, insert/delete 시 shifting 작업에 $O(n)$ 시간이 소요되기 때문이다.

sequence interface

종류	operation	Array $O()$	Linked List $O()$	Dynamic Array $O()$	Binary Tree $O()$
container	build(X)	$O(n)$	$O(n)$	$O(n)$	$O(n)$
static	get_at(i)/set_at(i,x)	$O(1)$	$O(n)$	$O(1)$	$O(h)$
dynamic	insert_first(x)/delete_first()	$O(n)$	$O(1)$	$O(n)$	$O(h)$
	insert_last(x)/delete_last()	$O(n)$	$O(n)$	$O(1_{(a)})$	$O(h)$
	insert_at(i,x)/delete_at(i)	$O(n)$	$O(n)$	$O(n)$	$O(h)$

Set에서는 hash table이 find(k)뿐만 아니라 insert(x), delete(k)를 하는데 $O(1)$ 시간이 걸린다. 위치와 상관없이 insert(x), delete(k)와 같은 dynamic operation을 $O(1)$ 시간에 수행할 수 있다는건 큰 장점이지만, hash table에도 단점이 있다. Find_prev/next(k), find_min/max()와 같은 연산에 $O(n)$ 시간이 걸리기 때문이다. 오히려 원소 간의 관계를 찾는 위와 같은 연산들은 sorted array가 각각 $O(logn), O(1)$ 시간으로 잘 찾아준다. 하지만 sorted array 역시 dynamic한 연산인 insert(x), delete(k)와 같은 연산을 $O(n)$ 시간에 수행하므로 단점이 뚜렷하다.

set interface

종류	operation	Array $O()$	Sorted Array $O()$	Direct Access Array $O()$	Hash Table $O()$	Binary Tree $O()$
container	build(X)	$O(n)$	$O(nlogn)$	$O(u)$	$O(n_{(e)})$	$O(nlogn)$
static	find(k)	$O(n)$	$O(logn)$	$O(1)$	$O(1_{(e)})$	$O(h)$
dynamic	insert(x)/delete(x)	$O(n)$	$O(n)$	$O(1)$	$O(1_{(a)(e)})$	$O(h)$
order	find_min()/find_max()	$O(n)$	$O(1)$	$O(u)$	$O(n)$	$O(h)$
	find_next(k)/find_prev(k)	$O(n)$	$O(logn)$	$O(u)$	$O(n)$	$O(h)$

여태 배운 것들을 정리해보니 각 interface에 요구되는 연산에 따라 비교우위에 있는 자료구조들이 다르고 통틀어서 좋은 하나의 자료구조가 있었으면 하는 생각이 든다. Binary tree가 바로 그 해결책이다. Binary tree는 build(X)를 제외한 모든 연산에 $O(logn)$ 시간이 걸리기 때문이다. Part1에서는 각 연산들에 $O(h)$ 시간이 걸린다는 것을 증명한다. 이후 Part2에서는 $h$ 가 곧 $O(logn)$ 임을 증명한다. 그럼으로써 비로소 binary tree에 대한 이해를 완성하게 된다.

Binary Trees

insert(x), delete(k)와 같은 동적 연산과 find(k)뿐만 아니라 find_prev/next(k), find_min/max()와 같은 탐색 연산을 효율적으로 하기 위해 item의 저장 방식에 대한 생각의 전환이 필요하다. 앞서 배웠던 자료구조들은 item을 저장하는 방식과 item을 읽어오는 순서가 일치하는 방식을 택했다. 생각의 전환을 위해 item을 저장하는 방식과 item을 읽어오는 순서를 분리시켜 item을 저장하는 방식에 대한 자유도를 높인다. 이때, 높아진 자유도를 최대한 활용하기 위해 item을 동적으로 저장해본다. 하지만 이렇게 되면 item을 읽어오는 순서가 불분명해진다. 혼란을 방지하기 위해 일관된 규칙 하에 item을 읽는다면 읽어온 item이 한 가지 순서로만 정렬이 될 것이다. 여기서 말하는 일관된 규칙이 바로 traversal order이다.

Item을 저장하는 방법에 대한 자율성을 확보한 상태에서, 어떠한 형태로 item을 저장하는 것이 가장 효율적일까를 고민해본다. 4.Hashing의 decision tree에서 단서를 얻을 수 있다. Comparison model에서 $find(k)$ 를 $O(logn)$ 보다 빠르게 연산할 수 없음을 decision tree의 높이를 구함으로써 증명했다. 이로부터 decision tree의 형태가 상당히 효율적이라는 것을 알 수 있는데, 이때 노드의 역할을 알고리즘 비교가 아닌 item 그자체를 저장하는 것으로 바꿔서 부여한다면 어떨지 생각해보자. Item 자체를 트리로 표현했기 때문에 단순히 $find(k)$ 가 아닌 $insert/delete$ 등 $build(X)$ 가 아닌 모든 연산을 효율적으로 수행할 수 있게 된다. 트리로 item을 저장하는 것이 왜 동적인지에 대해서는 Dynamic operations 부분에서 알게된다.

Item을 뜻하는 노드를 트리 형태로 저장하기 위한 방법에 대한 힌트는 linked list로부터 얻을 수 있다. 2. Data Structure에서 linked list에 대한 설명을 가져오면 다음과 같다.

Linked list는 각 원소를 node라는 단위에 저장한다. 
노드는 앞서 말한 것처럼 원소값과 다음 노드의 주소를 저장해야한다. 
따라서 원소값을 node.item에 저장하고, 다음 노드의 주소를 node.next에 저장한다.

Linked list와 같이 노드 간의 연결 고리를 pointer를 통해 만들어줘야 한다. 다만, linked list는 pointer가 다음 노드의 주소를 가리키는 1개의 next pointer만 있는 것에 반해 binary tree는 아래 그림의 보라색 선과 같이, 1개의 previous pointer와 2개의 next pointer를 필요로 한다.

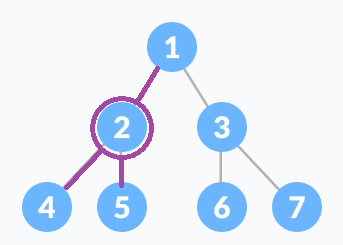
그림 출처: https://www.programiz.com/dsa/perfect-binary-tree

Binary tree의 binary node에게는 parent node를 가리키는 previous pointer 1개, left child와 right child를 가리키는 next pointer 2개, 총 3개의 pointer가 존재한다. 위의 그림에서 2번이 해당 binary node라고 하면 parent node는 1번 노드, left child는 4번 노드, right child는 5번 노드다.

class Binary_Node:				# O(1)
	def __init__(A, x):
    	A.item = x
        A.left = None
        A.right = None
        A.parent = None

용어 정리

root: parent node가 없는 노드(최상단에 위치함)
leaf: children node가 없는 노드(최하단에 위치함)
ancestor: 노드 x로부터 root 노드까지 도달하는데 거쳐가는 노드들
subtree: 노드 x를 root 노드로 하는 binary tree
depth: ancestor 노드의 수로, root노드로부터 노드 x까지 도달하기 위해 거쳐야 하는 edge의 수
height: x로부터 leaf까지의 경로 중 가장 길이가 긴 경로에 있는 edge의 수, 다시 말해서 노드 x의 subtree의 depth 중 최댓값

Traversal Operations

Traversal Order

앞서 일관된 규칙으로 binary tree의 순서를 정한다고 했었다. 여기서 말하는 일관된 규칙이 traversal order이고 다음과 같다.

node x의 왼쪽 subtree에 속하는 모든 노드는 x보다 먼저 온다.

node x의 오른쪽 subtree에 속하는 모든 노드는 x 이후에 온다.

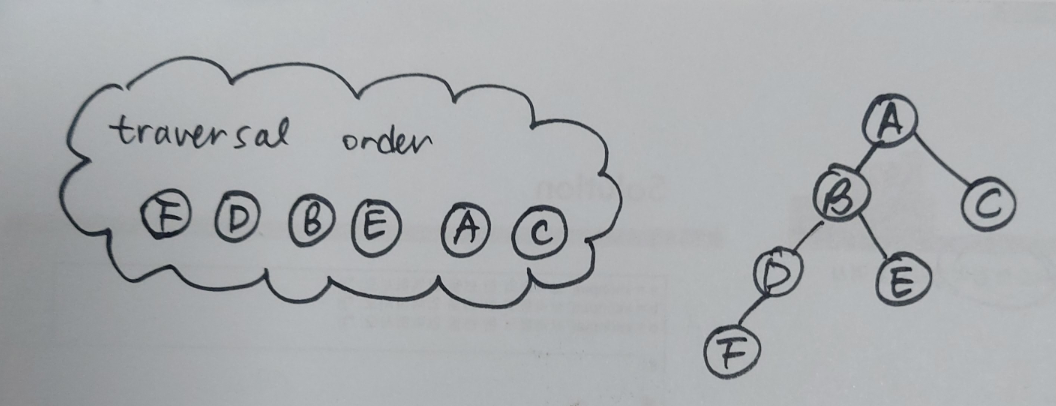
위의 그림에서 traversal order에 따라 노드의 순서를 나열해보면 F, D, B, E, A, C이다.

기준 노드 A에 대하여 코드를 작성해보면 흐름이 다음과 같다.

노드 A의 왼쪽 subtree에 속한 모든 노드를 iterate

노드 A 자체를 반환

노드 A의 오른쪽 subtree에 속한 모든 노드를 iterate

def subtree_iter(A):			# O(n)
	if A.left:
    	yield from A.left.subtree_iter()
    yield A
    if A.right:
    	yield from A.right.subtree_iter()

아직은 traversal order에 의미론적 의미를 부여하지 않았지만, set와 sequence interface에 적용하면서 부여해볼 것이다.

우선 $insert/delete$ 연산을 하기 위해 발판이 되는 이진트리 내에 특정 노드를 탐색하는 연산들을 정의할 것이다.

1. subtree_first(node)

Binary tree가 주어졌을 때, node A의 subtree에서 traversal order상 가장 처음/마지막에 나타나는 노드를 찾는다. Subtree에서 시작과 마지막 노드를 찾는 과정은 비슷하므로 시작 노드를 찾는 과정만 기술해본다.

Node A에게 left child가 존재한다면 계속 left로 이동한다. node = node.left Node A에게 left child가 존재하지 않는다면, 해당 노드를 binary tree에서 시작 노드이므로 노드를 반환한다.return node

def subtree_first(A):				# O(h)
	if A.left:
    	return A.left.subtree_first()
    else:
    	return A

참고로 subtree_last(node)의 코드는 다음과 같다.

def subtree_last(A):				# O(h)
	if A.right:
    	return A.right.subtree_last()
    else:
    	return A

Subtree_first는 계속 left child를 찾아가므로 binary tree의 아래 방향으로 탐색한다. 따라서, 소요되는 시간은 binary tree의 높이인 $O(h)$ 이다.

2. successor(node)

Binary tree에서의 노드가 주어졌을 때, traversal order에서의 다음 노드(successor)나 직전 노드(predecessor)를 찾는다. Successor과 predecessor를 찾는 과정 또한 유사하므로 successor를 찾는 과정만 기술해본다.

Successor를 찾는 과정은 두 가지 경우의 수로 나뉜다. 우선, 기준 노드 A에게 오른쪽 child가 있다면, if node.right A의 successor는 오른쪽 child의 subtree의 첫 번째 노드다. return subtree_first(node) 그에 반해 만일 기준 노드 A에게 오른쪽 child가 없다면 else A의 successor는 A의 subtree에 존재할 수 없다. 이때 취해야 할 행동은 노드의 ancestor 기준으로 해당 노드가 왼쪽 subtree에 위치할 때까지, node == node.parent.left tree의 위 방향으로 탐색해서 node=node.parent가장 낮게 존재하는 ancestor를 찾아야한다. return node

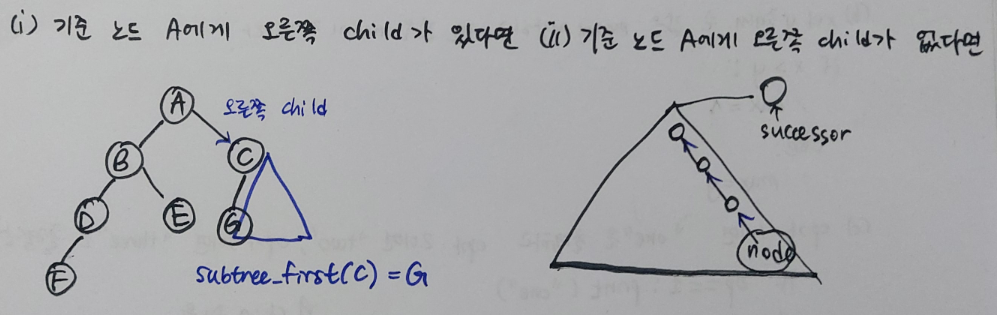
def sucessor(A):				# O(h)
	if A.right:
    	return A.right.subtree_first()
    # node == node.parent.left에 도달할 때까지
    while A.parent and (A is A.parent.right):
        A = A.parent
    return A.parent

Predecessor를 구하는 코드는 다음과 같다.

def predecessor(A):
	if A.left:
    	return A.left.subtree_last()
    # node == node.parent.right에 도달할 때까지
    while A.parent and (A is A.parent.left):
    	A = A.parent
    return A.parent

Sucessor 연산은 parent 노드로 이동할 때, binary tree의 윗방향으로 탐색한다. 따라서 소요되는 시간은 binary tree의 높이인 $O(h)$ 이다.

Dynamic Operations

동적 연산 $insert/delete$ 를 subtree_first/last와 successor/predecessor를 이용해서 구현해보자.

1. Insert

새로운 노드 B를 노드 A의 전 또는 후에 추가하는 로직을 가각 살펴볼 것이다.

1-1. subtree_insert_before(node_new)

노드 A에게 left child가 존재하지 않는다면 단순하게 노드 B를 노드 A의 left child로 추가하면된다. 하지만, 만일 노드 A에게 left child가 존재한다면 노드 A의 왼쪽 subtree의 마지막 노드의 right child로 노드 B를 추가한다.

def subtree_insert_before(A, B):		# O(h)
	if A.left:
    	A = A.left.subtree_last()
        A.right, B.parent = B, A
    else:
    	A.left, B.parent = A, B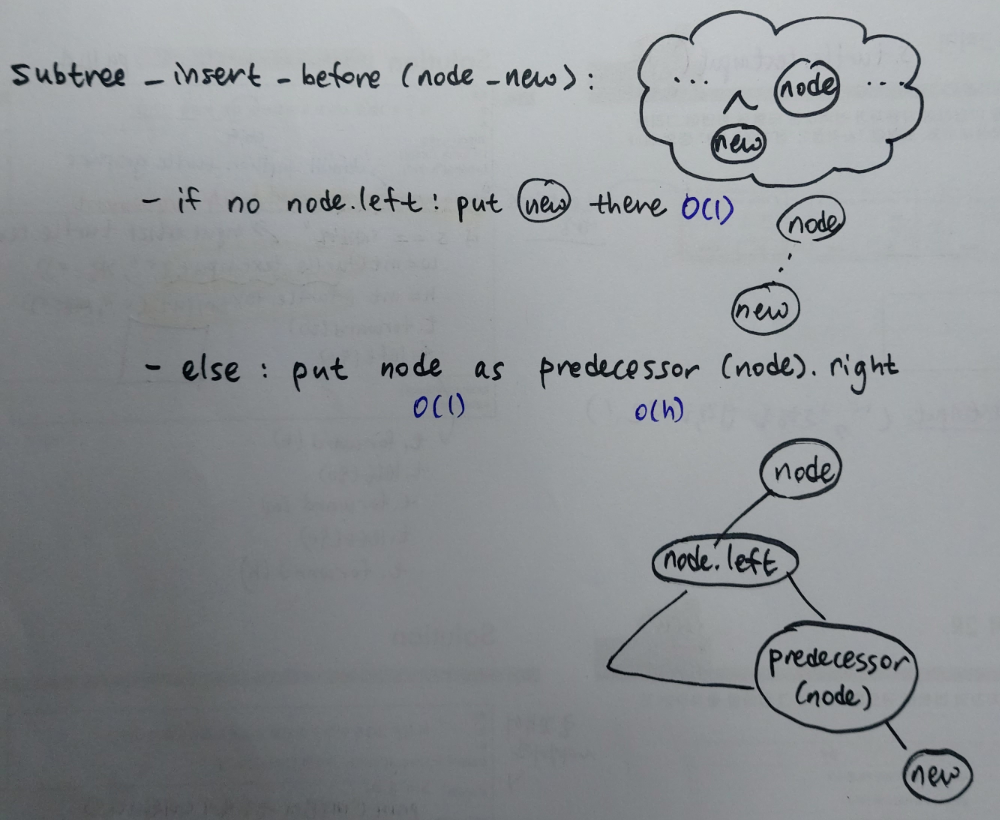

1-2. subtree_insert_after(node_new)

Subtree_insert_after(node_new)는 subtree_insert_before(node_new)에 대칭이다.노드 A에게 right child가 존재하지 않는다면 단순하게 노드 B를 노드 A의 right child로 추가하면된다. 하지만, 만일 노드 A에게 right child가 존재한다면 노드 A의 오른쪽 subtree의 첫번째 노드의 left child로 노드 B를 추가한다.

def subtree_insert_after(A, B):		# O(h)
	if A.right:
    	A = A.right.subtree_last()
        A.left, B.parent = B, A
    else:
    	A.right, B.parent = A, B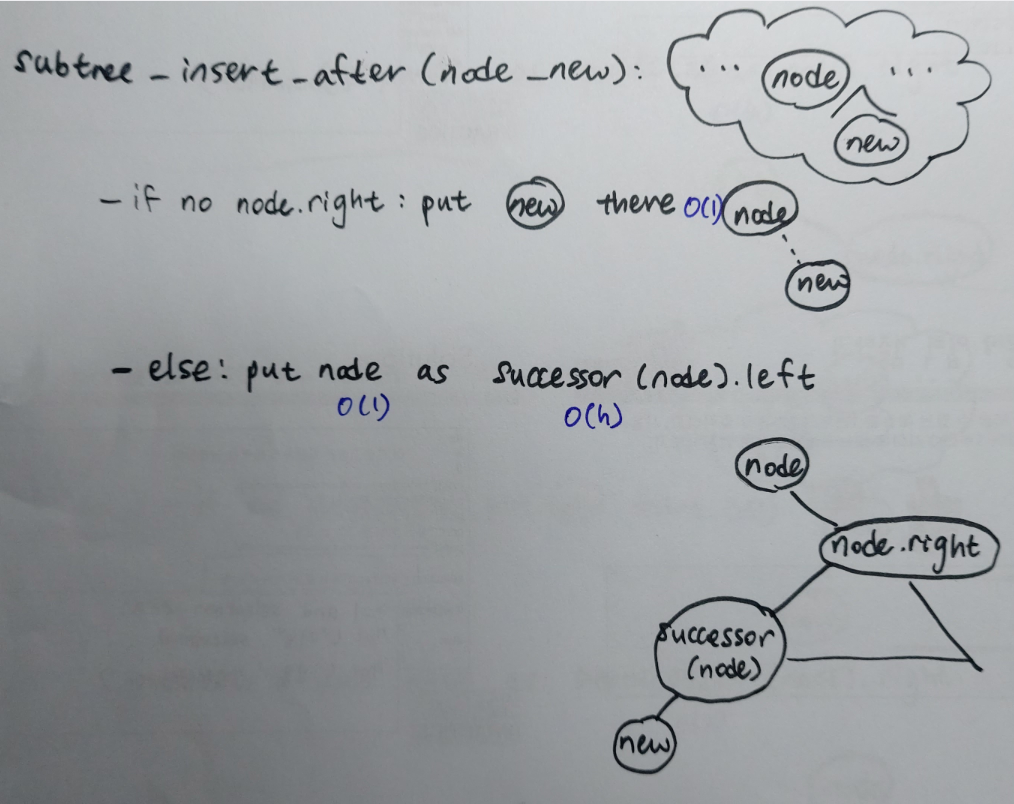

Insert 연산 역시 binary tree를 내려오면서 알고리즘을 수행하기 때문에 $O(h)$ 시간이 소요된다.

2. Delete

subtree_delete(node)

노드를 삭제하는 방법은 크게 두 가지 경우에 따라 달라진다. 우선 node가 leaf라면 바로 parent 노드의 해당 child 노드 포인터를 제거하면 된다. 만약, node가 leaf가 아니라면 해당 node의 item이 leaf에 속할 때까지 node의 sucessor나 predecessor과 계속 바꿔치기한다. 이 경우도 두 가지 경우의 수로 나눌 수 있는데, node.left가 존재한다면 해당 node의 item을 해당 노드의 predecessor의 item과 바꾼다. node.right가 존재한다면 해당 node의 item을 해당 노드의 successor의 item과 교환한다.

def subtree_delete(A):			# O(h)
	if A.left or A.right:		# A는 leaf가 아님
    	if A.left:
        	B = A.predecessor()
        else:
        	B = A.sucessor()
        A.item, B.item = B.item, A.item
        return B.subtree_delete()
    if A.parent:				# A는 leaf
    	if A.parent.left is A:
        	A.parent.left = None
        else:
        	A.parent.right = None
    return A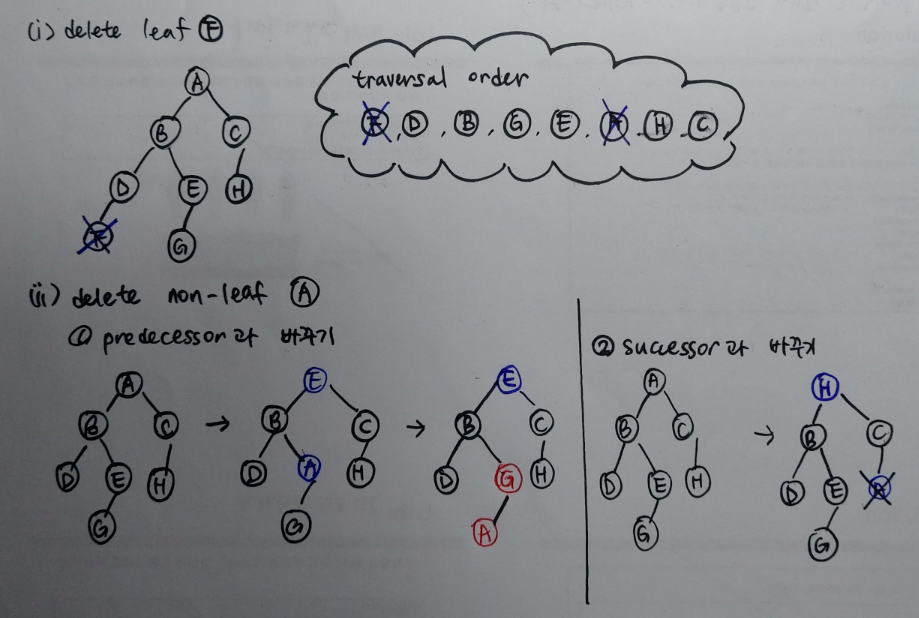

바꿔치기도 아래쪽으로만 진행되기 때문에 삭제 연산도 $O(h)$ 시간이 걸린다.

Binary node 전체 코드

class Binary_Node:
	def __init__(A, x):				# O(1)
    	A.item = x
        A.left = None
        A.right = None
        A.parent = None
        # A.subtree_update()
        
    def subtree_iter(A):			# O(n)
    	if A.left:
        	yield from A.left.subtree_iter()
        yield A
        if A.right:
        	yield from A.right.subtree_iter()
            
    def subtree_first(A):			# O(h)
    	if A.left:
        	return A.left.subtree_first()
        else:
        	return A
            
    def subtree_last(A):			# O(h)
    	if A.right:
        	return A.right.subtree_last()
        else:
        	return A
            
    def successor(A):				# O(h)
    	if A.right:
        	return A.right.subtree_first()
        while A.parent and (A is A.parent.right):
        	A = A.parent
        return A.parent
        
    def predecessor(A):				# O(h)
    	if A.left:
        	return A.left.subtree_last()
        while A.parent and (A is A.parent.left):
        	A = A.parent
        return A.parent
        
    def subtree_insert_before(A, B):# O(h)
    	if A.left:
        	A = A.left.subtree_last()
            A.right, B.parent = B, A
        else:
        	A.left, B.parent = B, A
            
    def subtree_insert_after(A, B):# O(h)
    	if A.right:
        	A = A.right.subtree_first()
            A.left, B.parent = B, A
            
    def subtree_delete(A):			# O(h)
    	if A.left or A.right:
        	if A.left:
            	B = A.predecessor()
            else:
            	B = A.successor()
            A.item, B.item = B.item, A.item
            return B.subtree_delete()
        if A.parent:
        	if A.parent.left is A:
            	A.parent.left = None
            else:
            	A.parent.right = None
        return A

Interface 적용

Binary tree 자료구조를 이제 set과 sequence interface에 도입해본다. Traversal order이 어떻게 정의되느냐에 따라 set interface인지 sequence interface인지 나뉜다.

Set

Set interface에 binary tree 자료구조를 대입한 것을 Set binary tree, 혹은 Binary Search Tree(BST) 라고 한다. Set binary tree는 traversal order를 오름차순으로 sorted된 key를 저장하는데에 사용한다.

BST property: 모든 노드에 대하여

left subtree의 모든 key $\leq$ 노드의 key $\leq$ right subtree의 모든 key

노드 x의 subtree에서 모든 노드를 key값으로 찾을 수 있게 되는데, binary search처럼 $O(h)$ 시간에 찾을 수 있게 된다.

key 값으로 노드를 찾는 법

노드 x의 key값보다 작다면: 왼쪽 subtree를 순환

노드 x의 key값보다 크다면: 오른쪽 subtree를 순환

해당되지 않는다면: 노드 x에 저장되어 있는 item을 반환

class BST_Node(Binary_Node):
	def subtree_find(A, k):			# O(h)
    	if k < A.item.key:
        	if A.left:
            	return A.left.subtree_find(k)
        elif k > A.item.key:
        	if A.right:
            	return A.right.subtree_find(k)
        else:
        	return A
        return None
        
    def subtree_find_next(A, k):	# O(h)
    	if A.item.key <= k:
        	if A.right:
            	return A.right.subtree_find_next(k)
            else: 
            	return None
        elif A.right:
        	B = A.left.subtree_find_next(k)
            if B:
            	return B
        return A
        
    def subtree_find_prev(A, k):	# O(h)
    	if A.item.key >= k:
        	if A.left:
            	return A.left.subtree_find_prev(k)
            else:
            	return None
        elif A.right:
        	B = A.right.subtree_find_prev(k)
            if B:
            	return B
        return A
    
    def subtree_insert(A, B):		# O(h)
    	if B.item.key < A.item.key:
        	if A.left:
            	A.left.subtree_insert(B)
            else:
            	A.subtree_insert_before(B)
        elif B.item.key > A.item.key:
        	if A.right:
            	A.right.subtree_insert(B)
            else:
            	A.subtree_insert_after(B)
        else:
        	A.item = B.item
            
class Set_Binary_Tree(Binary_Tree): # Binary Search Tree
	def __init__(self):
    	super().__init__(BST_Node)
        
    def iter_order(self):
    	yield from self
        
    def build(self, X):
    	for x in X:
        	self.insert(x)
            
    def find_min(self):
    	if self.root:
        	return self.root.subtree_first().item
            
    def fin_max(self):
    	if self.root:
        	return self.root.subtree_last().item
            
    def find(self, x):
    	if self.root:
        	node = self.root.subtree_find(k)
            if node:
            	return node.item
                
    def find_next(self, k):
    	if self.root:
        	node = self.root.subtree_find_next(k)
            if node:
            	return node.item
                
    def find_prev(self, k):
    	if self.root:
        	node = self.root.subtree_find_prev(k)
			if node:
            	return node.item
                
    def insert(self, x):
    	new_node = self.Node_Type(x)
        if self.root:
        	self.root.subtree_insert(new_node)
            if new_node.parent is None:
            	return False
        else:
        	self.root = new_node
        self.size += 1
        return True
        
    def delete(self, k):
    	assert self.root
        node = self.root.subtree_find(k)
        assert node
        ext = node.subtree_delet()
        if ex.parent is None:
        	self.root = None
        self.size -= 1
        return ext.item

Sequence

Sequence의 경우 traversal order를 sequence 순서를 저장하는데에 사용한다. Binary tree로 sequence를 도입하기 위해 각 노드에 추가적으로 저장해야 할 요소들이 있기 때문에 set interface보다 다소 복잡하다. 따라서 다음 강의에서 정리한다.