MIT 6.006 Introduction to Algorithms 10강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=U1JYwHcFfso&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=10

9강에서 다룰 interface와 data structure

• interface: sequence, (set)
• data structure: binary tree

6강 복습 + 이번에 배울 것

6강에서 subtree_insert_before/after, subtree_delete, subtree_first/last, predecessor/successor를 모두 $O(h)$시간이 걸린다는 것을 확인하였다. 여기서 주의해야 할 것은 binary tree의 모양에 따라서 $O(h)$가 최악의 경우, $O(n)$이 될 수 있다는 점이다. Linked list와 같이 하나의 긴 사슬 모양의 binary tree가 이러한 경우에 해당된다. 그래도 희소식은 만일 binary tree가 거의 완벽히 대칭을 이룰 경우, $O(h)$가 $O(logn)$ 이 된다는 점이다. 그런데 처음 binary tree 모양이 완벽히 대칭이라고 하더라도 노드를 추가하거나 삭제하게 되었을 때 대칭이 깨지게된다. 따라서 이때 binary tree의 모양을 대칭으로 만들기 위한 장치가 바로 rotation이다.

Interface 적용

앞서 6강에서 traversal order을 어떻게 정의되느냐에 따라 set interface인지 sequence interface인지 나뉜다고 했었다.

set

traversal order: 오름차순으로 sorted된 key

BST property

• left subtree의 모든 key $\leq$ 노드의 key $\leq$ right subtree의 모든 key

Set interface를 구현한 코드는 6. Binary Trees, Part1에서 찾아볼 수 있다. 핵심만 다시 짚어보면 subtree_find(node,k) 연산은 이진트리에서 작동하도록 이진 탐색을 일반화한 것이다. 다만 다른 자료구조, 예를 들어 sorted array에서의 이진 탐색과의 차별점은 동적으로 오름차순으로 정렬된 key를 유지시킬 수 있다는 것이다.

종류	operation	Array $O()$	Sorted Array $O()$	Direct Access Array $O()$	Hash Table $O()$	Binary Tree $O()$
container	build(X)	$O(n)$	$O(nlogn)$	$O(u)$	$O(n_{(e)})$	$O(nlogn)$
static	find(k)	$O(n)$	$O(logn)$	$O(1)$	$O(1_{(e)})$	$O(logn)$
dynamic	insert(x)/delete(x)	$O(n)$	$O(n)$	$O(1)$	$O(1_{(a)(e)})$	$O(logn)$
order	find_min()/find_max()	$O(n)$	$O(1)$	$O(u)$	$O(n)$	$O(logn)$
	find_next(k)/find_prev(k)	$O(n)$	$O(logn)$	$O(u)$	$O(n)$	$O(logn)$

sequence

traversal order: sequence order

Sequence의 경우 traversal order가 sequence의 순서와 같은데, sequence의 순서는 extrinsic하게 부여된다. 따라서 각 item의 특성이 아닌 순서를 통해 i번째 item을 찾아야한다. 참고로, set에서의 increasing key가 이와 같은 역할을 담당했다. 다시 돌아와서, 만약에 왼쪽 subtree에 몇개의 item이 저장되어있는지 알 수 있다면, 왼쪽 subtree의 size를 우리가 찾고자하는 노드의 subtree size와 비교할 수 있게된다. 이를 통해 왼쪽, 오른쪽 subtree 중 어느 방향에 찾고자 하는 노드가 있을지 알아낼 수 있다. 요약해보면. binary tree를 sequence interface에 활용하기 위해 subtree에 추가적인 요소를 저장해야하고, 이 추가적인 요소는 노드의 subtree size다.

property

• 노드의 size: 해당 노드를 root로 하는 subtree에 속한 노드의 수

Subtree_at(node, i)을를 코드를 구현하기 위한 로직은 다음과 같다.

• subtree_at(node,i):
  - $n_L$: node.left의 크기
  • i < $n_L$: subtree_at(node.left, i)
  • i = $n_L$: node 반환
  • i > $n_L$: subtree_at(node.right, i-$n_L$-1)

class Size_node(Binary_Node):
	def subtree_update(A):		# O(1)
    	super().subtree_update()
        A.size = 1
        if A.left:
        	A.size += A.left.size
        if A.right:
        	A.size += A.right.size
            
    def subtree_at(A, i):
    	assert 0 <= i
        if A.left:
        	L_size = A.left.size
        else:
        	L_size = 0
        if i < L_size:
        	return A.left.subtree_at(i)
        elif i > L_size:
        	return A.right.subtree_at(i - L_size - 1)
        else:
        	return A

Binary tree를 도입한 sequence에서 특정 노드를 찾을 때 역시 아래 방향으로 탐색을 하기 때문에 $O(h)$ 시간이 소요된다.

종류	operation	Array $O()$	Linked List $O()$	Dynamic Array $O()$	Binary Tree $O()$
container	build(X)	$O(n)$	$O(n)$	$O(n)$	$O(n)$
static	get_at(i)/set_at(i,x)	$O(1)$	$O(n)$	$O(1)$	$O(logn)$
dynamic	insert_first(x)/delete_first()	$O(n)$	$O(1)$	$O(n)$	$O(logn)$
	insert_last(x)/delete_last()	$O(n)$	$O(n)$	$O(1_{(a)})$	$O(logn)$
	insert_at(i,x)/delete_at(i)	$O(n)$	$O(n)$	$O(n)$	$O(logn)$

Subtree Augmentation

Binary tree에 추가적인 요소를 저장하는 방법을 subtree augmentation이라고 한다. 앞서 size는 subtree에 augment할 수 있는 특성 중 하나이다. 여기서 잠깐 size를 왜 굳이 binary tree에 별도로 저장하는지에 대한 이유를 파헤쳐본다. 우리는 앞서 sequence interface에서 노드를 찾는 시간을 $O(h)$가 걸린다고 했었다. 만약 트정 노드를 찾기 위해 사전에 binary tree의 모든 노드의 크기를 구해야한다면 노드 전체를 훑어봐야 하므로 $O(n)$ 시간이 걸릴 것이다. 이는 배보다 배꼽이 큰 셈이다. 따라서 노드의 크기를 $O(1)$시간에 구할 수 있도록 각 노드에 해당 정보를 저장, augment하는 것이다.

subtree augmentation property

• 각각의 노드는 $O(1)$ 시간에 접근할 수 있는 field나 속성을 가진다.
• subtree property(node)는 해당 노드와 해당 노드의 children으로부터 $O(1)$시간에 구할 수 있다.
  - node.size = node.left.size + node.right.size + 1

그렇다면 어떤 속성들이 subtree에 augment하기에 적합할까? Subtree augmentation에 적합한 속성들은 전역 속성이 아닌 요소들이다. 전역 속성이란 하나의 노드에서 속성을 바꾸게 되면 모든 노드의 속성이 바뀌는 것이다. 따라서, index와 depth와 같은 요소들은 subtree property가 될 수 없고 height는 subtree property가 될 수 있다.

Binary tree에 노드를 추가/삭제를 하면서 subtree에 augmentation한 속성들에 대해 업데이트를 해줘야한다. 전역 속성이 아니기 때문에 binary tree 전체가 아닌 변경된 노드의 조상들에 대해서만 업데이트하면 된다.

Balanced Binary Trees

Height Balance

앞서 binary tree가 거의 완벽히 대칭을 이룰 경우, $O(h)$가 $O(logn)$ 이 된다고 하였다. 거의라고 표현한 이유는 binary tree를 구성하는 노드의 갯수에 따라 완벽하게 대칭이 아닐 때가 생기기 때문이다. 그럼에도 불구하고 왼쪽 subtree와 오른쪽 subtree의 높이가 최대 1 차이가 날 때 가능한 범위 내에 최대 대칭을 이룬다고 간주하고 이를 height-balanced된 상태라고 한다. 아래의 그림이 height balanced 된 상태이다. 노드 6을 기준으로 왼쪽 subtree의 높이가 0, 오른쪽 subtree의 높이가 1으로 1 차이가 나므로 대칭이다.

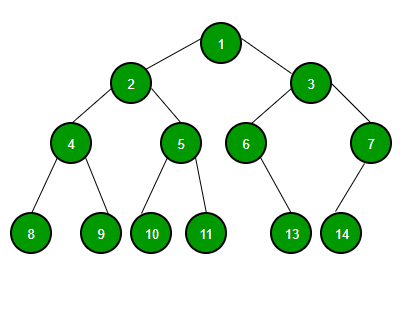
사진 출처: https://www.geeksforgeeks.org/binary-tree-data-structure/

왼쪽 subtree와 오른쪽 subtree의 높이 차이를 skew라고 하며 정확한 정의는 다음과 같다.

skew = height(node.right) - height(node.left)
height balance = height(node.right) - height(node.left) $\in$ {-1, 0, 1}

Height balance가 되어있는지 확인하기 위해 매번 높이를 계산하기보단 height를 subtree augmentation으로 저장함으로써 height를 구하는 시간을 단축한다. 즉, 노드를 추가 및 삭제할 때 각 노드당 $O(1)$시간으로 노드를 업데이트 할 수 있다. 하지만 총 h개의 ancestor를 업데이트해줘야 하므로 총 소요 시간은 $h*O(1)$이다. 참고로 node의 height를 구하는 방법은 다음과 같다.

• node.height = 1 + max{node.left.height, node.right.height}

Height balanced => balanced

잠시 height balanced되었다는 것의 의미가 balanced를 의미한다는 위의 명제를 증명해보자. 균형이 잡혔다는 것의 의미는 $h = O(logn)$를 의미한다. 이는 곧 $n = 2^{\Omega(h)}$이다.

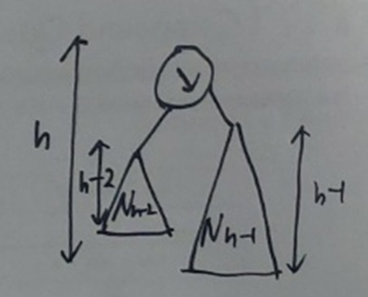
• $N_h$: height balanced tree에서의 노드의 수

$N_h= N_{h-1} + N_{h-2} + 1$
$> N_{h-2} + N_{h-2}$
$= 2*N_{h-2}$
$=2^{h/2}$
이는 곧 $h \leq 2logn$이므로 $h = O(logn)$이 성립한다.

Rotation

노드를 제거하거나 leaf에 새로운 노드를 추가함에 따라 height balance가 깨진다. 이때 traversal order를 유지한 채 균형을 다시 찾아주는 작업을 rotation이라고 한다.

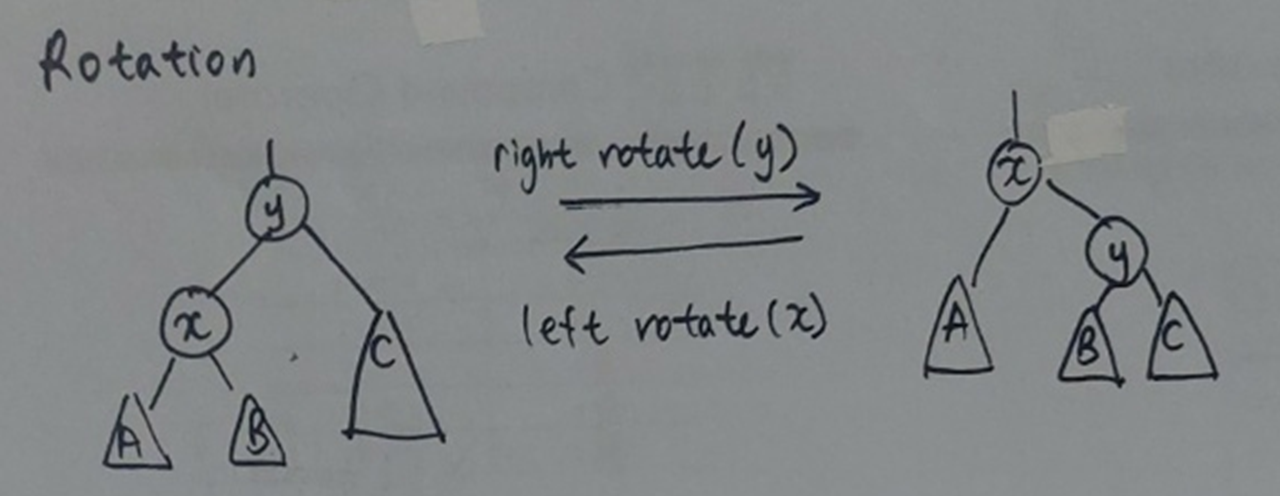
예시를 통해 unbalanced 노드 x의 균형을 rotation을 통해 회복하는 과정을 살펴본다.

• 총 문제 상황: skew(x) = 2

• 1번째 상황: skew(y) = 1
  

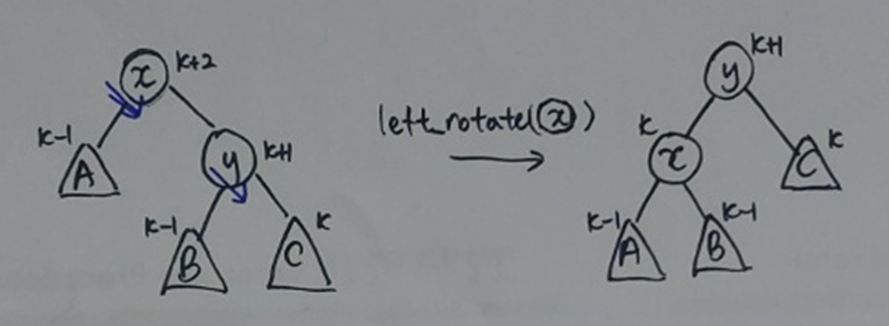
• 2번째 상황: skew(y) = 0
  

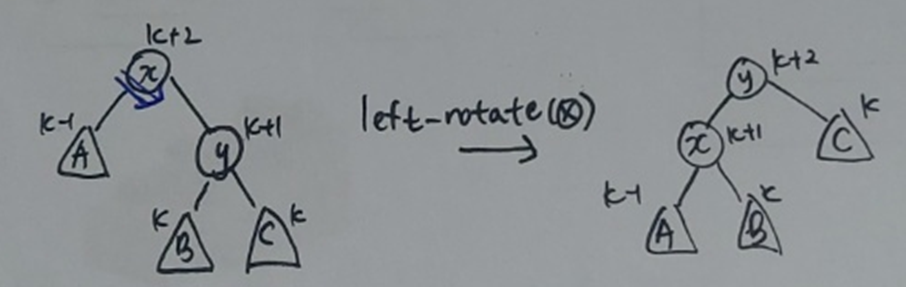
• 3번째 상황: skew(y) = -1
  

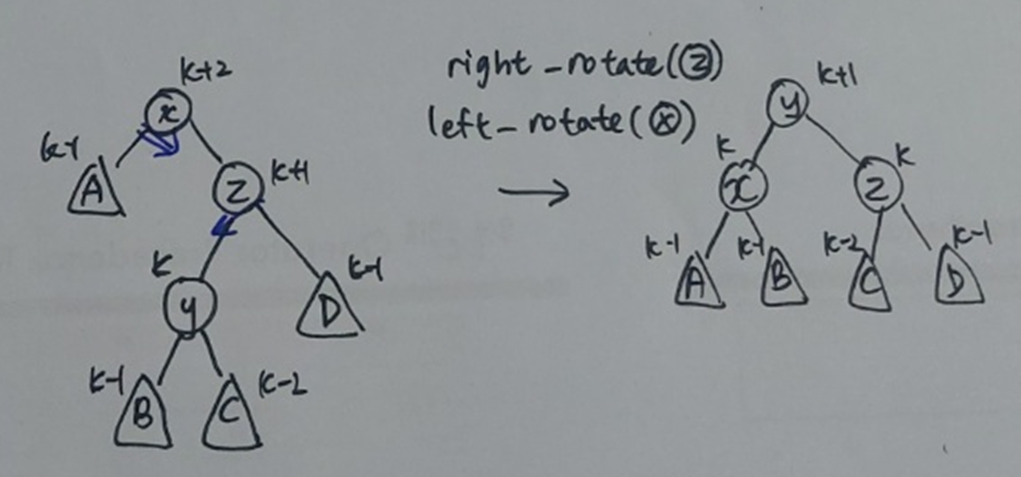
Part2에서 height balance가 유지된다면 $h = O(logn)$임을 증명하였다. 다시 말해서, binary tree는 set interface와 sequence interface의 $build(X)$를 제외한 모든 연산을 전반적으로 효율적으로 수행한다. 따라서, 특정 연산에 한해서만 효율적인 다른 자료구조들에 비해 확실한 이점을 갖는다.