[MIT 6.006] 8. Binary Heaps ( 이진 힙 )

Aacara·2023년 5월 9일

자료구조 및 알고리즘

목록 보기

8/13

MIT 6.006 Introduction to Algorithms 12강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=Xnpo1atN-Iw&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=12

9강에서 다룰 interface와 data structure

interface: priority queue

data structure: dynamic array, sorted dynamic array, set AVL Tree, binary heap

P. Priority Queue Interface

Priority queue interface는 set interface의 부분 집합이다. 이는 곧 priority queue interface가 set interface에서 가능한 연산 중 일부만 구현한다는 뜻이고 정의된 연산들은 다음과 같다.

build(X): X에 있는 item들로 초기화

insert(x): x를 추가

delete_max(): 가장 큰 key의 item을 반환함과 동시에 삭제

find_max(): 가장 큰 key의 item을 반환

class PriorityQueue:
	def __init__(self):
    	self.A = []
        
    def insert(self, x):
    	self.A.append(x)
        
    def delete_max(self):
    	if len(self.A) < 1:
        	raise IndexError('pop from empty priority queue')
        return self.A.pop()
        
    @classmethod
    def sort(Queue, A):
    	pq = Queue()
        for x in A:
        	pq.insert(x)
        out = [pq.delete_max() for _ in A]
        out.reverse()
        return out

Priority queue는 set의 부분 집합이기 때문에 key값을 기준으로 우선순위를 정한다. 또한 가장 큰 원소를 하나씩 반환하거나 삭제한다. 따라서, 매번 가장 큰 원소를 반환하기 위해선 정렬 알고리즘이 필요하다. 참고로, priority queue는 delete_max(), find_max() 대신 delete_min(), find_min()을 수행할 수도 있다.

Priority Queue Data Structure	build(A)	insert(x)	delete_max()
Dynamic Array	$O(n)$	$O(1_a)$	$O(n)$
Sorted Dynamic Array	$O(nlogn)$	$O(n)$	$O(1_a)$
Set AVL Tree	$O(nlogn)$	$O(logn)$	$O(logn)$
Binary Heap	$O(n)$	$O(logn_a)$	$O(logn_a)$

Priority Queue Sort

Priority queue sort는 다음과 같은 절차를 통해 이루어진다.

build(A), 또는 A에 있는 원소 x에 대해 insert(x)
그 후, delete_max()를 반복적으로 수행

여기서 실질적으로 정렬을 하는 과정은 모두 자료 구조 내에서 실행되기 때문에 원소 삽입과 가장 큰 원소 삭제 및 반환만으로도 정렬이 가능하다.

실행 시간
$T_{build}(n) + nT_{deleteMax} \leq n(T_{insert} + T_{deleteMax})$

여태 다루었던 정렬 알고리즘 중 많은 것들은 위의 실행시간을 만족시키는 priority queue sort로 볼 수 있다. 각 자료구조에 따라 어떻게 정렬이 이루어지고 궁극적으로 Binary Heap가 priority queue sort에 왜 가장 적합한지 설명한다.

Priority Queue Data Structure	Priority Queue Sort O()	Priority Queue Sort In-place
Dynamic Array	$O(n^2)$	Y
Sorted Dynamic Array	$O(n^2)$	Y
Set AVL Tree	$O(nlogn)$	N
Binary Heap	$O(nlogn)$	Y

S. Data Structures for the implementation of Priority Queue Interface/Sort

S-1. Dynamic Array

Priority Queue Data Structure	build(A)	insert(x)	delete_max()	Priority Queue Sort O()	Sort In-place
Dynamic Array	$O(n)$	$O(1_a)$	$O(n)$	$O(n^2)$	Y

Priority Queue Interface
정렬이 되지 않은 dynamic array의 경우 insert(x)를 할 때 array의 마지막에 원소를 추가해주면 되기 때문에 $O(1)$ 이 걸린다. 그에 반해 delete_max()는 모든 원소를 탐색하면서 최댓값을 찾아준 후, 마지막 원소값과 바꾼 후 삭제하므로 $O(n)$ 시간이 걸린다.
Priority Queue Sort
Dynamic array 자료구조에서의 priority queue sort는 곧 selection sort와 같다.

selection sort
1. $A[:i + 1]$ 에서 가장 큰 수를 찾는다.
2. 가장 큰 수와 $A[i]$ 와 바꾼다.
3. recursive하게 $A[:i]$ 를 정렬한다.

자세한 설명은 https://velog.io/@aacara/3-Sorting에서 확인하자.

S-2. Sorted Dynamic Array

Priority Queue Data Structure	build(A)	insert(x)	delete_max()	Priority Queue Sort O()	Sort In-place
Sorted Dynamic Array	$O(nlogn)$	$O(n)$	$O(1_a)$	$O(n^2)$	Y

Priority Queue Interface
Sorted dynamic array의 경우 insert(x)를 할 때 array의 마지막에 원소를 추가한 후, 정렬 순서에 맞는 위치로 이동시킨다. 정렬 순서에 맞는 위치로 이동시킬 때 이진탐색을 사용하여 $O(logn)$ 시간 안에 맞는 위치를 찾을 수 있으나, shifting 작업이 불가피하므로 $O(n)$ 시간이 걸린다. 그에 반해 sorted dynamic array에서 가장 큰 원소는 마지막 원소이므로 delete_max()에 $O(1)$ 시간이 걸린다.

Priority Queue Sort
Sorted dynamic array 자료구조에서의 priority queue sort는 곧 insertion sort와 같다.

insertion sort
1. recursive하게 $A[:i]$ 를 정렬한다.
2. $A[:i]$ 까지 정렬되었다는 전제하에 $A[:i + 1]$ 를 정렬한다.

자세한 설명은 https://velog.io/@aacara/3-Sorting에서 확인하자.

S-3. Set AVL Tree

Priority Queue Data Structure	build(A)	insert(x)	delete_max()	Priority Queue Sort O()	Sort In-place
Set AVL Tree	$O(nlogn)$	$O(logn)$	$O(logn)$	$O(nlogn)$	N

Priority Queue Interface
Dynamic array와 sorted dynamic array의 경우 insert(x), find_max()에 각각 하나의 연산에는 성능이 좋고 나머지에는 성능이 안좋다. 양 극단의 성능을 보이는 두 자료구조로부터 벗어나 insert(x), find_max()에 모두 적당한 성능을 보이는 자료구조가 바로 set AVL tree다.

Set AVL Tree는 build(X)를 제외한 모든 연산, insert(x), find_min(), find_max(), delete_min(), delete_max()에 $O(logn)$ 시간이 걸린다. 이때, 만약 subtree augmentation을 이용해서 가장 큰 key의 item을 subtree이 모든 노드에 저장한다면 find_min()과 find_max() 연산에 $O(1)$ 시간이 걸릴 것이다.

Priority Queue Sort
Set AVL tree 자료구조에서의 priority queue sort는 곧 AVL sort와 같다.

AVL Sort
1. n개의 item을 삽입한다.
각 item을 삽입할 때마다 $O(logn)$ 시간이 걸리므로 총 $O(nlogn)$ 시간이 걸린다.
2. travsersal order 순서대로 값을 읽어온다
모든 원소를 읽어야하므로 $O(n)$ 시간이 걸린다.

S-4. Binary Heaps⭐

Priority Queue Data Structure	build(A)	insert(x)	delete_max()	Priority Queue Sort O()	Sort In-place
Binary Heap	$O(n)$	$O(logn_a)$	$O(logn_a)$	$O(nlogn)$	Y

Priority Queue Interface
Set AVL tree의 경우 insert(x)와 delete_max()에 $O(logn)$ 시간이 걸리고 Priority queue sort를 하는데에 $\textbf{O(nlogn)}$ 시간이 걸린다는 장점이 있다. 다만, in-place 알고리즘이 아니라는 점이 아쉽다.

in-place 알고리즘

추가적인 메모리 공간을 거의 사용하지 않고 수행하는 알고리즘

Priority queue sorting을 하는데에 $\textbf{O(nlogn)}$ 시간이 걸리면서도 in-place 정렬이 가능하도록 하는 자료구조가 binary heap이다. Binary heap는 연산을 $O(logn)$ 시간에 하기 위해 tree 구조를 가져오면서도 in-place 정렬을 위해 array 구조도 참고했다.

Priority Queue Sort
Binary heap 자료구조에서의 priority queue sort는 곧 heap sort와 같다.
Heap sort를 이해하기 위해 우선 binary heap의 구조 및 연산에 대해 정리한 후 다시 돌아온다.

S-4_1. Binary Heap 구조

Binary heap 구조는 연산을 $O(logn)$ 시간에 할 수 있도록 항상 균형을 이루는 완전한 이진트리 구조를 가져온다. 다만 Binary tree와 다른 점은 메모리 공간에 포인터를 이용한 트리 구조를 저장하는 것이 아니라 key값을 담고 있는 array를 저장한다는 것이다. 얼핏 보면 array를 저장하는 것과 완전한 이진트리 구조를 가져온다는 것은 모순처럼 보인다. 하지만 저장 방식과 저장하고자하는 구조를 분리한다면 두 명제는 양립 가능하다. 저장되는 자료구조는 array이지만 array에 저장된 정보를 바탕으로 함축적으로 이진트리를 구성하면 된다. 저장된 array로부터 이진트리를 구성하는 원칙이 있는데 다음과 같다.

depth i에는 기본적으로 $2^i$ 개의 노드가 존재한다.

예외적으로 가장 큰 depth에는 노드가 $2^i$ 개 존재하지 않을 수도 있으나, 최대한 왼쪽에 노드를 배치한다.

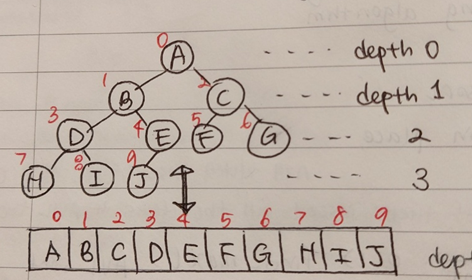
참고로, 그림에서는 0번 인덱스부터 시작했지만, 실제로는 0번 인덱스부터 시작하지 않는다. 아래 식들을 연산할 때 복잡해지기 때문이다.

Binary heap는 array만 저장할뿐 포인터를 저장하지 않는다. 그럼에도 불구하고 이진트리를 구성하는 것이 가능한 이유는 left child, right child 및 parent 노드를 산수를 통해 구할 수 있기 때문이다.

$left(i) = 2i+1$

$right(i) = 2i+2$

$parent(i) =$ ${i-1}\over2$

def parent(i):
	p = (i-1) // 2
    return p if 0<i else i
    
def left(i, n):
	l = 2 * i + 1
    return l if 1<n else i

def right(i, n):
	r = 2 * i + 2
    return r if r<n else i

S-4_2. Binary Heap 정의

Binary heap의 핵심 아이디어는 국소적으로 더 큰 key값을 이진트리의 상단에 위치시키는 것이다. 이러한 속성을 Max-Heap Property라고 한다.

Max-Heap Property

i 노드에서,
$Q[i] \geq Q[j], j \in \{left(i), right(i)\}$

결론적으로 binary Heap Q는 완전한 binary tree를 함축하는 array Q로, 모든 노드 i에서 Max-Heap Property를 만족한다. 따라서, key 값이 가장 큰 item은 루트 노드에 위치한다.

S-4_3. Binary Heap 연산

Priority Queue Data Structure	build(A)	insert(x)	delete_max()	Priority Queue Sort O()
Binary Heap	$O(n)$	$O(logn_a)$	$O(logn_a)$	$O(nlogn)$

1. Heap Insert

가장 먼저 binary heap를 생성해야하므로 heap insert 연산을 살펴본다. Heap insert는 다음과 같은 과정을 통해 이루어진다.

Q: insert_last(x)

max_heapify_up(|Q| - 1)

1-1) insert_last(x)

새로운 item x를 dynamic array의 마지막에 추가하는 작업은 amortized $O(1)$ 시간이 걸린다. 하지만, 해당 원소가 max-heap property를 만족시키지 않을 수도 있으므로 만족시키는 위치로 이동시켜야 한다.

1-2) max_heapify_up(i)

max_heapify_up(i)은 Max-heap property를 만족시킬 때까지 해당 노드를 parent 노드와 바꾸는 작업을 진행한다. 구체적으로 다음과 같은 과정을 통해 이루어진다.

$Q[parent].key \geq Q[i].key$ 인지 확인한다.

만일 $Q[parent].key < Q[i].key$ 라면 $Q[parent].key$ 와 $Q[i].key$ 를 교환한다.

parent 노드에 대하여 재귀적으로 위 작업을 반복한다.

// 가정: A[:n]의 모든 노드는 max-heap property를 만족한다.
def max_heapify_up(A, n, c):
	p = parent(c)
    if A[p].key < A[c].key:
    	A[c], A[p] = A[p], A[c]
        max_heapify_up(A, n, p)

아래 그림에서 볼 수 있듯이, 각 subtree에 속한 노드의 key 값들은 해당 subtree에 속한 root 노드의 key 값보다 작다. 또한 parent 노드보다 상단에 있는 노드들의 key값은 parent 노드의 key값보다 크다. 따라서, 아래 그림과 같이 parent 노드의 key 값(5)를 삽입된 노드의 key 값(10)과 바꿨을 때 나머지 노드는 신경쓸 필요 없이, 기존의 parent 노드의 위치에서 재귀적으로 parent 노드와의 비교를 진행하면 된다.

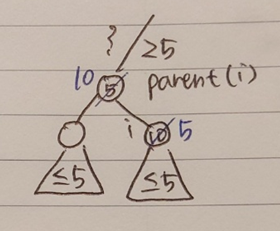
Insert_last(x) 연산에 $O(1)$ 시간이 걸리고 max_heapify_up(i) 연산이 윗방향, 즉 단방향으로만 진행된다. 따라서, insert(x) 연산은 이진트리의 높이인 $O(h)=O(logn)$ 시간이 걸린다.

2. Heap Delete Max

Key 값이 가장 큰 item이 루트 노드에 위치하기 때문에 find_max()는 바로 알 수 있다. Priority queue에서는 delete_max()가 중요한데 find_max()와 달리 루트 노드를 바로 삭제하는 것은 어렵다. 가장 삭제하기 쉬운 노드는 leaf 중에서도 가장 우측에 있는 노드이다. 따라서, 루트 노드와 leaf의 가장 우측에 있는 노드를 바꾼 후 삭제해야 한다. 일련의 과정을 정리하면 다음과 같다.

Q[0]과 Q[|Q|-1]을 바꾼다.

Q.delete_last()

max_heapify_down(0)

2-1) delete_last()

루트 노드와 마지막 노드를 바꿨으므로 마지막 노드의 key값이 가장 크다. 따라서, 마지막 노드를 삭제하면 된다. 하지만 루트 노드와 마지막 노드를 바꾸는 과정에서 루트 노드의 값이 가장 큰 값이 아닌 기존의 leaf노드의 값으로 바뀌었으므로 max-heap property가 깨졌다.

2-2) max_heapify_down(i)

max_heapify_down(i)은 Max-heap property를 만족시킬 때까지 해당 노드를 child 노드와 바꾸는 작업을 진행한다. 구체적으로 다음과 같은 과정을 통해 진행된다.

$j \in \{left(i), right(i)\}$ 에서 $Q[j].key$ 를 최대화할 수 있는 $j$ 를 고른다.

$Q[i].key \geq Q[j].key$ 인지 확인한다.

만일 $Q[i].key < Q[j].key$ 라면 $Q[i].key$ 와 $Q[j].key$ 를 교환한다.

j 노드에 대하여 재귀적으로 위 작업을 반복한다.

// 가정: A[:n]의 모든 노드는 max-heap property를 만족한다.
def max_heapify_down(A, n, p):
	l,r = left(p, n), right(p, n)
    c = l if A[r].key < A[l].key else r
    if A[p].key < A[c].key:
    	A[c], A[p] = A[p], A[c]
        max_heapify_down(A, n, c)

아래 그림을 살펴보면 max_heapify_up(i)일 때와 반대로 max_heapify_down(i)일때는 해당 노드를 자식 노드와 바꿔야한다. 여기서, 왼쪽 자식 노드와 오른쪽 자식 노드 중 가장 key 값이 더 큰 자식 노드와 해당 노드를 바꿔야 한다. 그 이유는 key 값이 작은 노드와 바꾼다면 부모 노드보다 자식 노드의 key값이 더 커지기 때문이다.

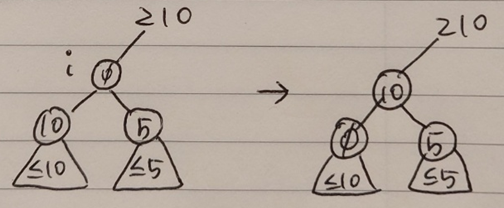
Delete_last() 연산에 $O(1)$ 시간이 걸리고 max_heapify_down(i) 연산이 아랫 방향, 즉 단방향으로만 진행된다. 따라서, delete_max() 연산은 이진트리의 높이인 $O(h)=O(logn)$ 시간이 걸린다.

3. Heap Sort

Heap insert에서 추가된 마지막 노드의 위치를 max_heapify_up(i)를 통해 이진 트리의 위쪽 방향으로 이동시켰던 것처럼 heap delete max에선 루트 노드의 위치를 max_heapify_down(i)를 통해 이진 트리의 아래쪽 방향으로 이동시킨다. 그렇기 떄문에 insert와 delete_max연산에는 각자 $O(logn)$ 시간이 소요된다. 종합해보면, n개의 요소에 대해 insert를 한 후, delete_max()를 하면 정렬이 되어 heap sort에는 $O(nlogn)$ 시간이 걸린다.

class PQ_Heap(PriorityQueue):
	def insert(self, **args):		# O(logn)
    	super().insert(*args)
        n, A = self.n, self.A
        max_heapify_up(A, n, n-1)
        
    def delete_max(self):			# O(logn)
    	n, A = sef.n, self.A
        A[0], A[n] = A[n], A[0]
        max_heapify_down(A, n, 0)
        return super().delete_max()

S-4_4. 다른 자료구조에 비해 Binary Heaps가 가진 장점

S-4_4.1 In-Place Heaps

만일 Priority queue sort를 하는데 $O(nlogn)$ 시간이 걸리는 것만이 중요했다면 set AVL tree 자료구조를 사용하면 되기 때문에 binary heap라는 새로운 자료구조를 배우지 않았을 것이다. Binary heap가 binary tree에 비해 우위에 있는 이유는 binary heap를 토대로하는 정렬 알고리즘인 heap sort가 in-place 알고리즘이기 때문이다. In-place 알고리즘은 추가적인 메모리 공간을 필요로 하지 않아 메모리 자원을 효율적으로 쓰기 때문에 이롭다.

Heap sort가 in-place 방식으로 정렬을 하는 과정을 살펴본다. 우선 array A의 앞부분을 max-heap Q라고 한다. 처음에는 |Q|는 0이 된다. 그러다가 insert를 계속 하여 모든 원소를 Q에 추가하면 |Q|=|A|가 된다. 그 후, delete max를 계속 수행하면 |Q|는 다시 0이 된다. 결국 Q는 A 이상의 공간을 필요로 하지 않기 때문에 in-place 알고리즘이다.

S-4_4.2 O(n) Build Heap

Heap sort가 set AVL tree에 비해 가지는 이점이 추가적으로 더 존재한다. Build(A)를 하는데에 set AVL tree가 $O(nlogn)$ 시간이 걸리는 반면에 binary heap은 $O(n)$ 시간이 걸린다.

앞서 max heap priority queue를 이용해서 반복된 insertion을 max_heapify_up(i)를 통해 한다면 build(A)에 $\displaystyle\sum_{i=0}^{n-1}depth(i) = \displaystyle\sum_{i=0}^{n-1}logi = logn!= O(nlogn)$ 시간이 걸린다. 하지만 array를 완전한 binary tree로 처음부터 간주한다면 max_heapify_down(i)을 통해 A를 만들 수 있다. 수식을 통해 이해해보면 build(A)는 $\displaystyle\sum_{i=0}^{n-1}height(i) = \displaystyle\sum_{i=0}^{n-1}(logn - logi) = log \frac{n^n}{n!} = O(log(\frac{n^n}{\sqrt{n}(\frac{n}{e})^n})) = O(log\frac{e^n}{\sqrt{n}}) = O(nloge-log\sqrt{n}) = O(n)$ 이다.