로봇을 공부할 때 필요한 coordinate transformation(좌표계 변환)은 크게 두 가지로 나뉜다.

1. Translation(평행 이동)
2. Rotation(회전 이동)

1. Translation

아래와 같은 상황이 있다.

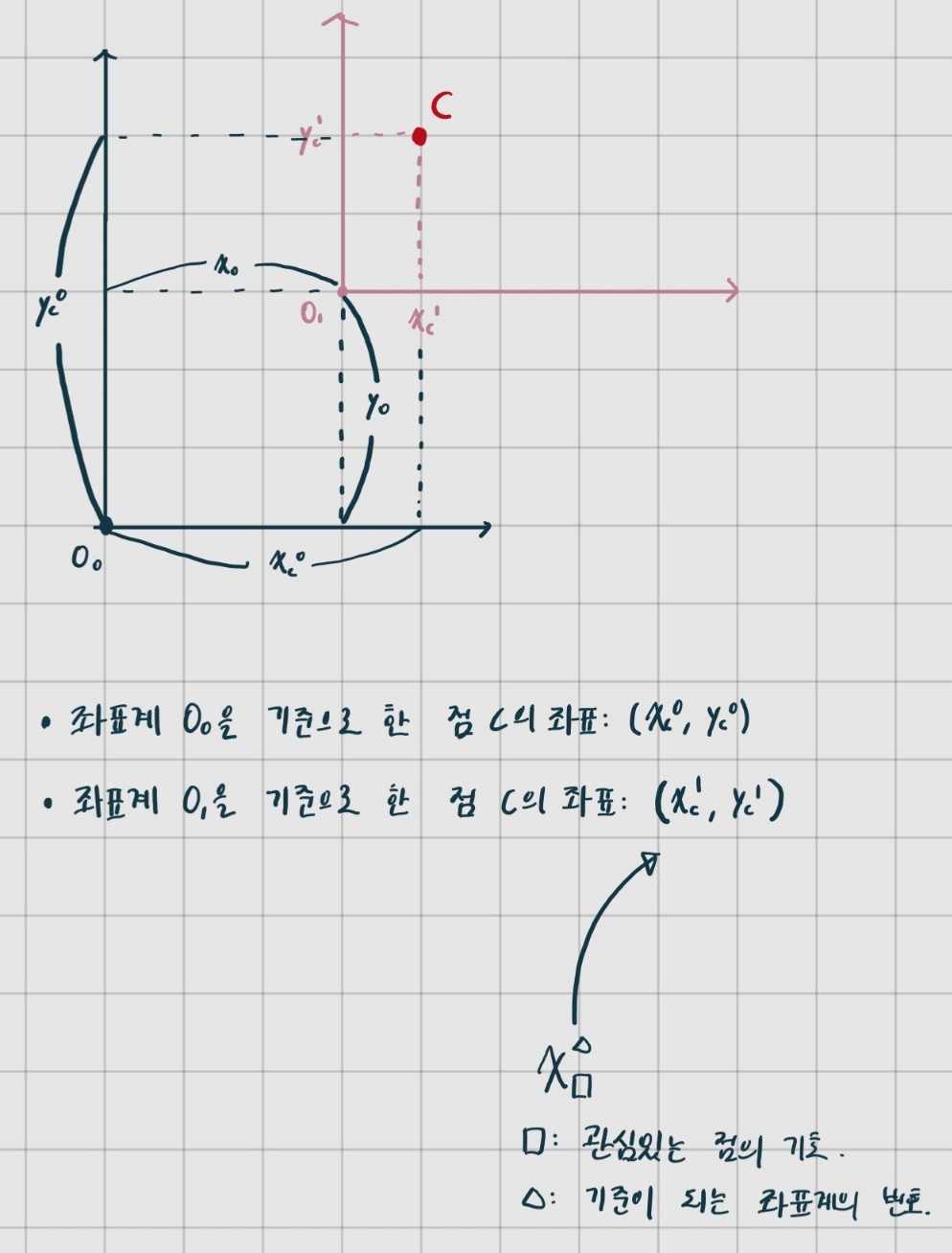
좌표계가 평행 이동한 상황이다.

$(x_C^1, y_C^1)$을 알고 $(x_C^0, y_C^0)$을 모르는 상황에서, 어떻게해야 $(x_C^0, y_C^0)$을 구할 수 있을까? 즉 좌표계 $O_1$에서 점 $C$의 좌표를 알고 좌표계 $O_0$에서 점 $C$의 좌표를 어떻게 구할 수 있을까? 방법은 간단하다.

좌표계 원점 $O_1$과 $O_0$ 사이의 거리를 더해주면된다. 직관적으로 이해가 된다.
이를 더 formal하게 표현하자면,

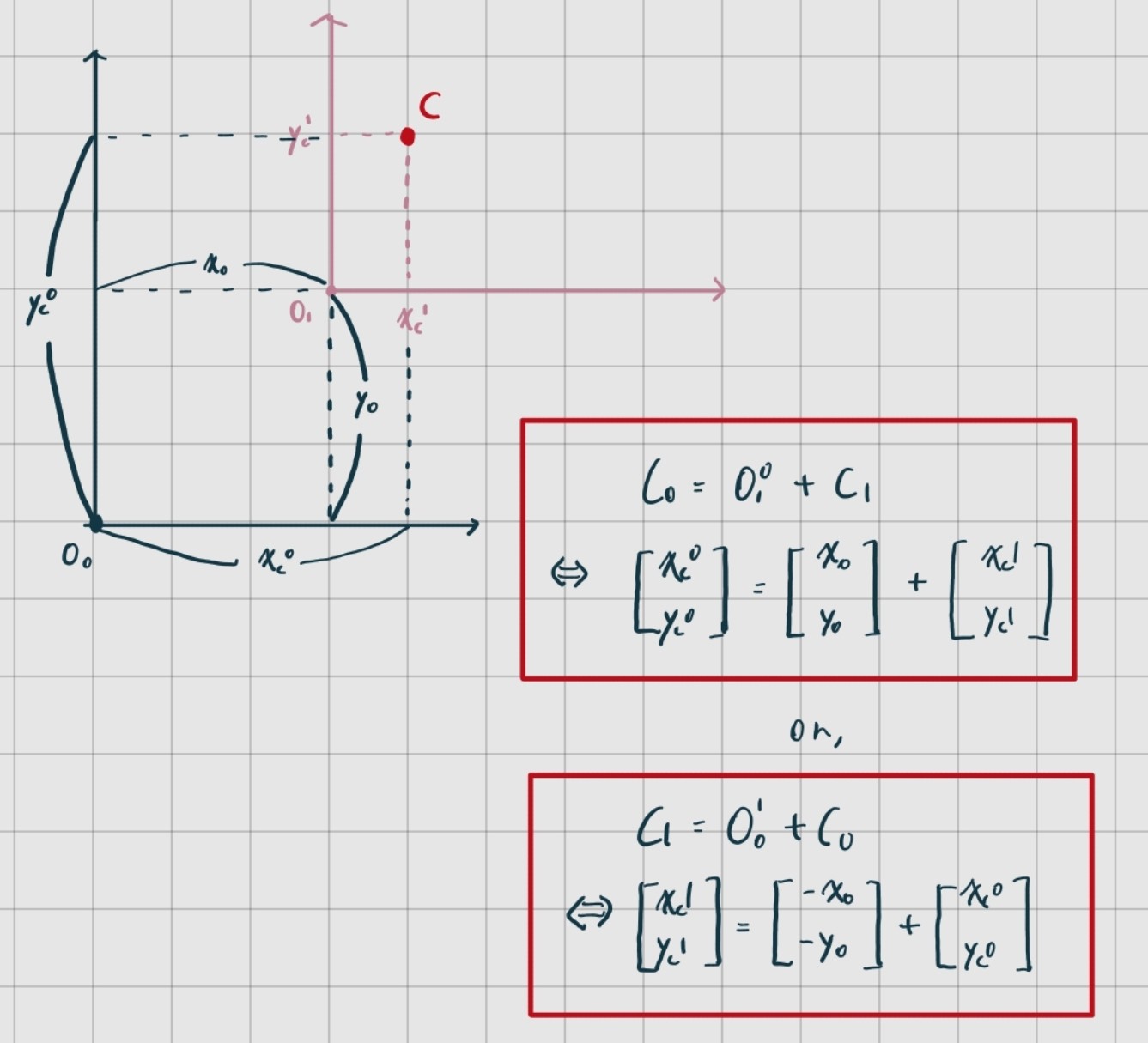
위와 같이 정리할 수 있다.

2. Rotation

아래와 같은 상황이 있다.

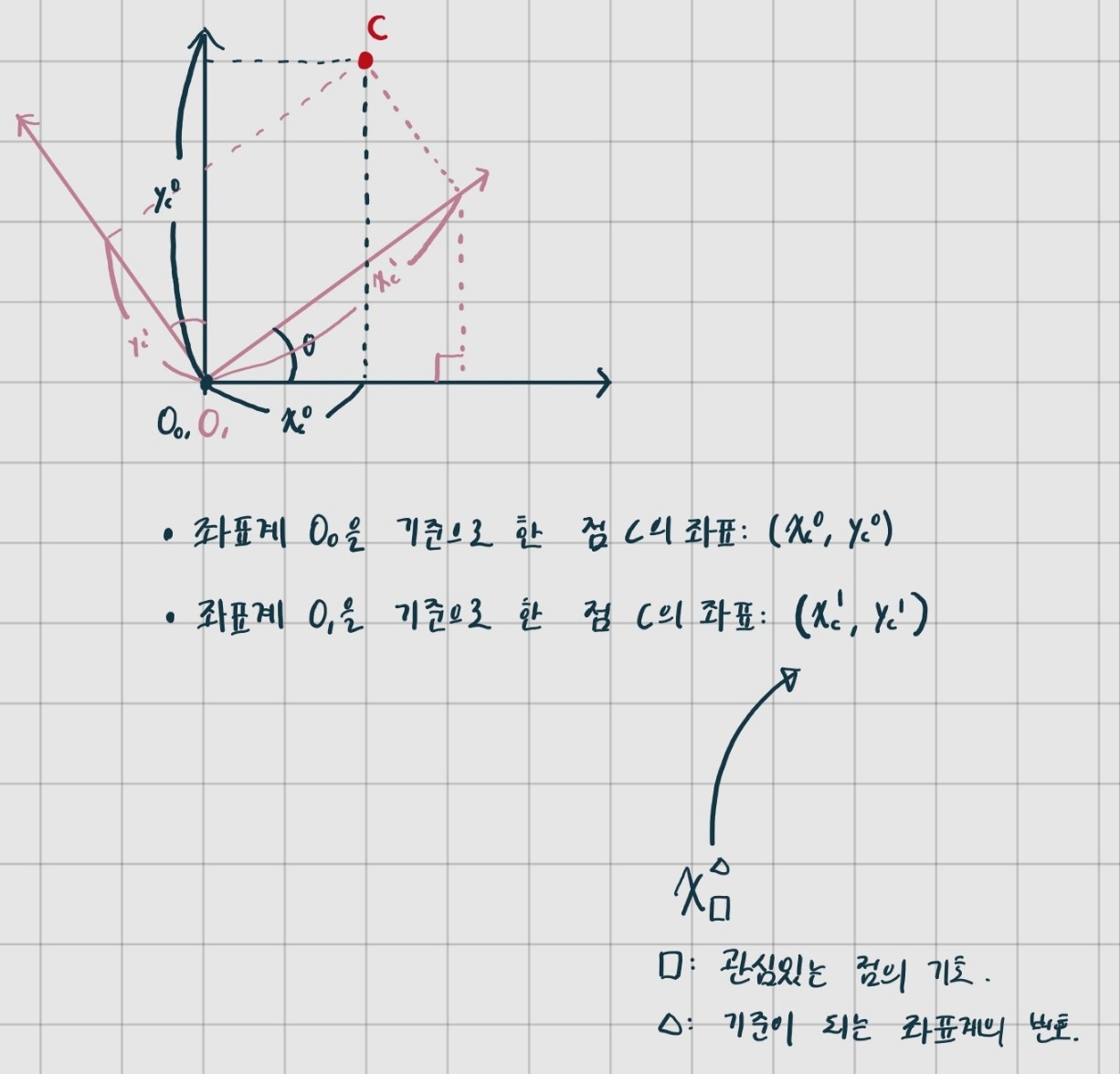
좌표계가 회전 이동한 상황이다.

마찬가지로, $(x_C^1, y_C^1)$을 알고 $(x_C^0, y_C^0)$을 모르는 상황에서, 어떻게해야 $(x_C^0, y_C^0)$을 구할 수 있을까? 추가적으로 각 $\theta$도 알고있다고 가정하자. 방법은 아래와 같다.


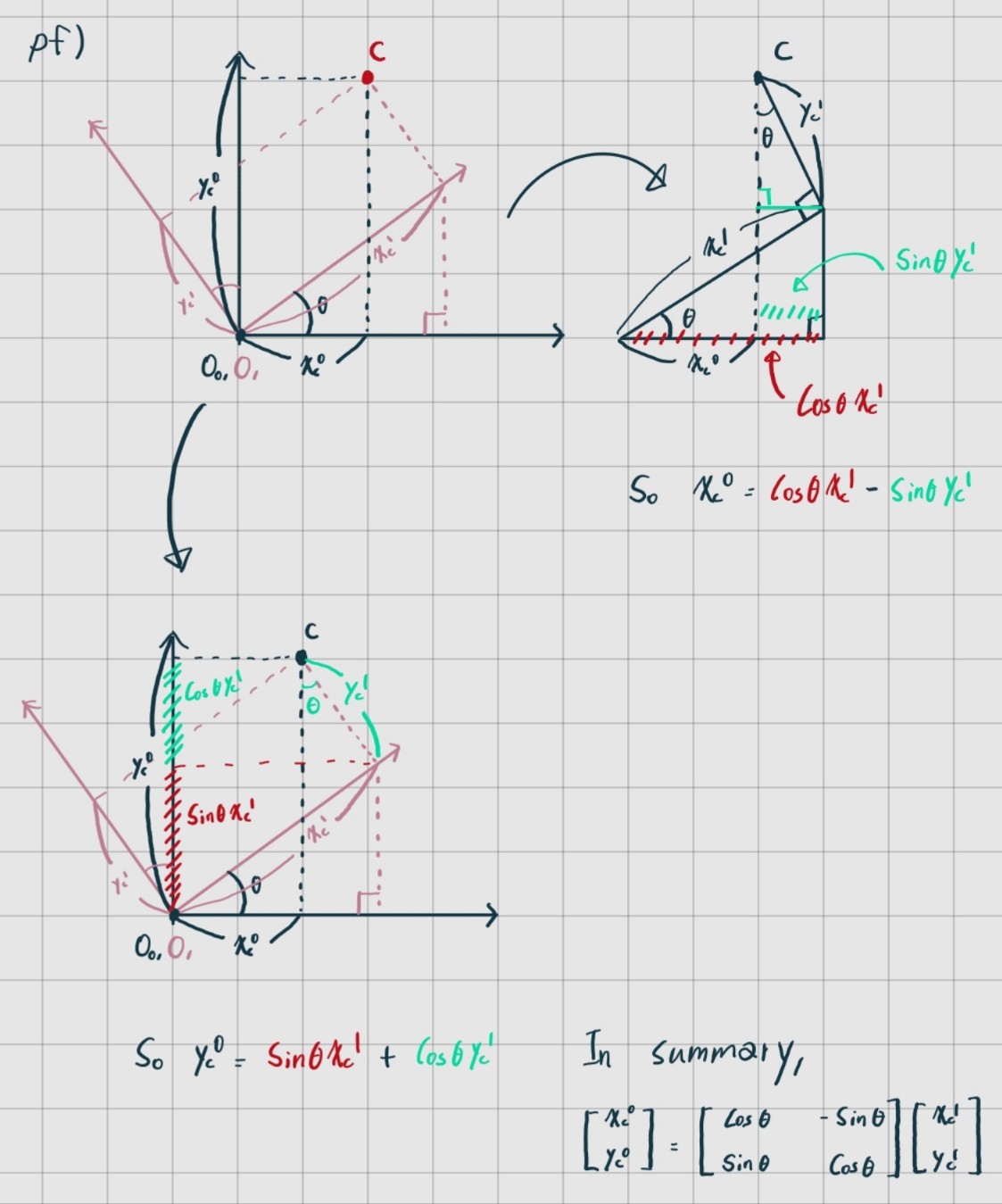
삼각함수로 구성된 행렬을 곱해주면 된다.
공식을 좀 더 formal하게 표현하자면,

위와 같이 정리할 수 있다.

더불어 rotation 행렬은 아래와같은 특수한 성질을 가진다.

3. Homogeneous Matrix

Translation과 Roation이 동시에 이루어진다면 좌표계 변환은 아래의 수식과 같다.

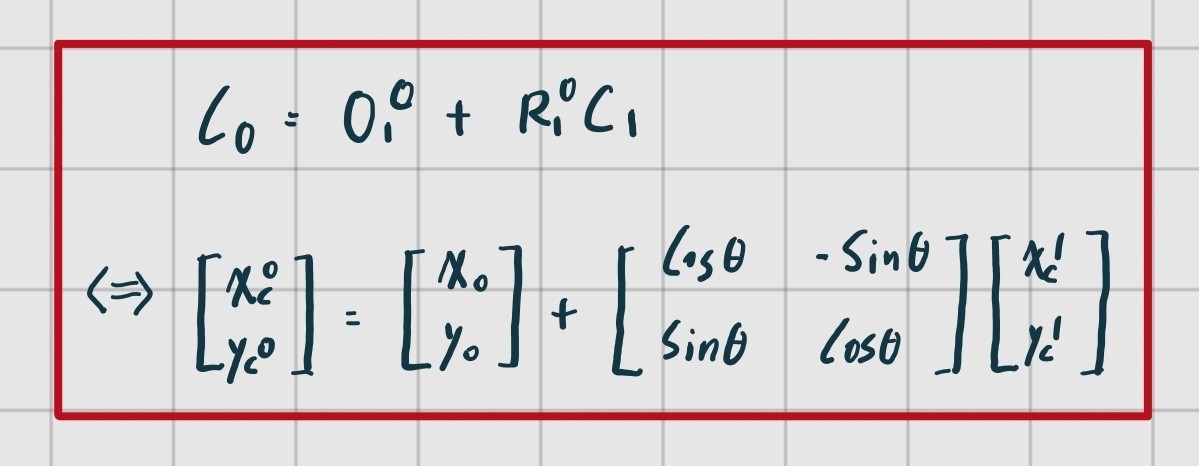
이때 $O$를 더해주고 $R$을 곱하는 2번의 연산이 실행되는데, Homogeneous Matrix 개념을 도입하면 이를 1번의 행렬 연산으로 단축할 수 있다.

(homogeneous linear system과는 상관없는 개념인듯하다)

위의 예시는 한번의 좌표계 변환을 하기에 연산을 줄이는 것이 별로 의미없게 보일 수도 있지만, 좌표게 변환을 N번 해야하는 상황에서는 연산을 유의미하게 줄일 수 있다.

마지막으로, homogeneous matrix는 아래의 성질을 가진다.

---

Reference: 모두의 로보틱스 2강(Homogeneous Matrix and numpy)(https://roadbalance.teachable.com/courses/5cee42/lectures/48650227)

질문, 조언 환영합니당 ■