로봇 중에서도 바퀴, 다리 등을 지녀 이동할 수 있는 로봇을 Mobile Robot이라고 부른다.

그 중에서도 우리가 흔히 볼 수 있는 로봇청소기와 같이 바퀴가 2개 달려 전진, 후진, 회전이 가능하나 수평 이동이 불가능한 mobile robot을 Differential Drive Mobile Robot이라고 부른다.

1. Forward Kinematics

DD mobile robot의 기본적인 state는 아래와 같다.

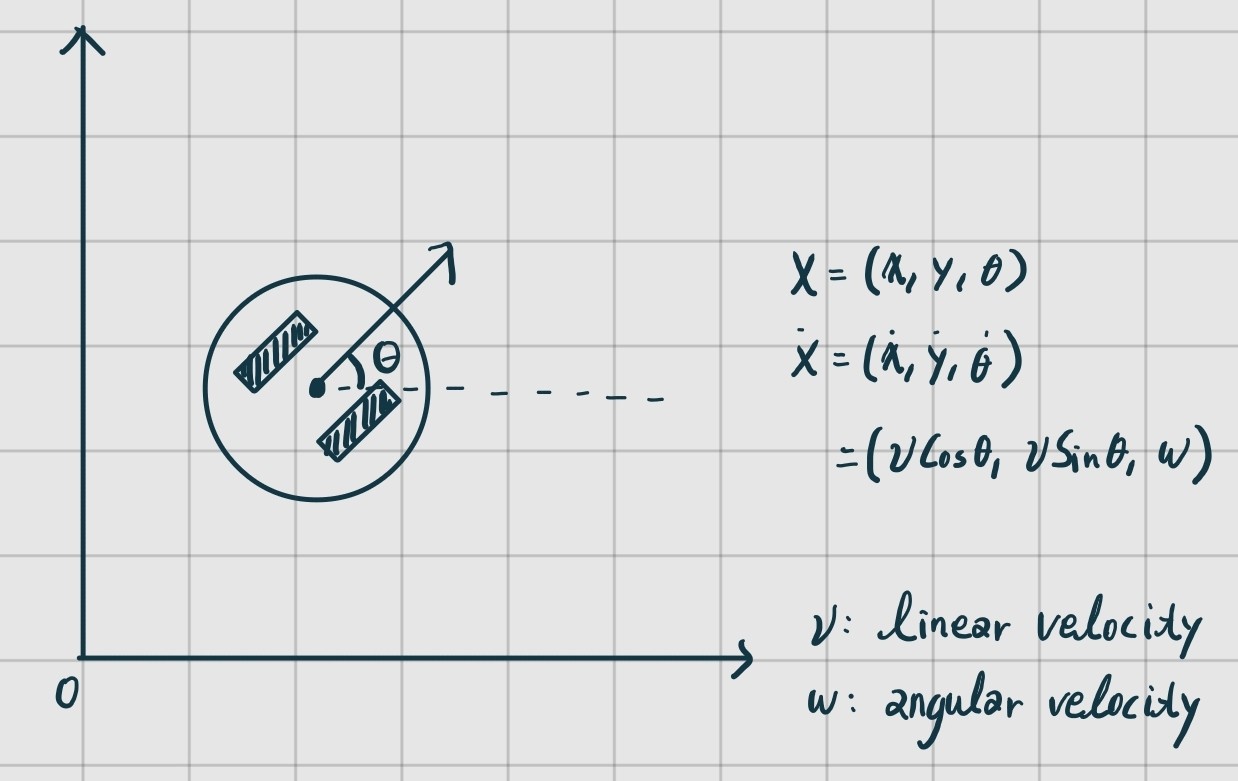
이때 $v\cos(\theta), v\sin(\theta)$는 극좌표와 관련이 있다.

이제 forward kinematics를 해보자. 로봇팔에서는 각도가 주어졌을 때 좌표를 얻는 게 f.kinematics 였다면, dd mobile robot에서는 $v$와 $\omega$가 주어졌을 때 $(x, y, \theta)$를 얻는 게 f.kinematics이다.

이때 Euler's Method를 사용하는데, 식을 적으면 아래와 같다.

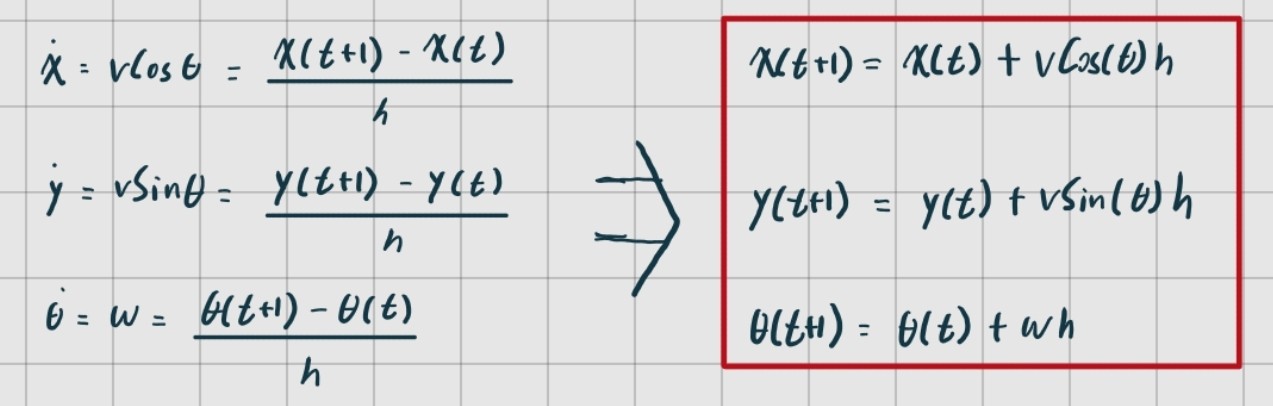
위의 식을 매 timestep마다 계산하면 로봇의 변화하는 state를 얻을 수 있게되며, 이것이 f.kinematics가 되는 것이다.

코드를 통해 구현해보자.

import math
from matplotlib import pyplot as plt
import numpy as np

def euler_integration(tspan, z0, u):    # euler integration 정의
    v, omega = u     					# 선속도와 각속도의 정보는 u 안에 있다
    h = tspan[1] - tspan[0]
    x0, y0, theta0 = z0

    xdot_c = v * math.cos(theta0)
    ydot_c = v * math.sin(theta0)
    thetadot = omega

    x1 = x0 + xdot_c * h
    y1 = y0 + ydot_c * h
    theta1 = theta0 + thetadot * h

    return [x1, y1, theta1]    			# t+1 timestep의 state를 반환

def motion_simulation():
    z0 = [0, 0, -math.pi/2]    			# 로봇의 초기 state 선언

    t1 = np.arange(0, 1, 0.1)
    t2 = np.arange(1, 2, 0.1)
    t3 = np.arange(2, 3, 0.1)

    t = np.append(t1, t2)
    t = np.append(t, t3)

    u = np.zeros((len(t), 2))

    for i in range(0, len(t1)):
        u[i, 0] = 1
    for i in range(len(t1), len(t1) + len(t1)):
        u[i, 1] = math.pi/2				# 각속도 부여
        u[i, 0] = 1
    for i in range(len(t1) + len(t2), len(t)):
        u[i, 0] = 1

    z = np.array(z0)

    for i in range(0, len(t)-1):
        z0 = euler_integration([t[i], t[i+1]],
                               z0,
                               [u[i, 0], u[i, 1]])
        z = np.vstack([z, z0])

    return t, z

def animate(t, z):						# 애니메이션 구현 함수

    R = 0.1

    for i in range(0, len(t)):
        x, y, theta = z[i]

        x2 = x + R*np.cos(theta)
        y2 = y + R*np.sin(theta)

        robot,  = plt.plot(x, y, color='green', marker='o', markersize=15)
        line, = plt.plot([x, x2], [y, y2], color='black')
        shape, = plt.plot(z[0:i, 0], z[0:i, 1], color='red')

        plt.xlim(-2, 2)
        plt.ylim(-2, 2)
        plt.gca().set_aspect('equal')
        plt.pause(0.1)
        line.remove()
        robot.remove()
        shape.remove()

if __name__ == '__main__':				# 프로그램 실행

    try:
        timestamps, precalculated_state = motion_simulation()
        animate(timestamps, precalculated_state)
    except Exception as e:
        print(e)
    finally:
        plt.close()

2. Robot Movement in World Frame

Inverser kinematics로 넘어가기 이전에, world frame과 robot frame 간의 관계에 대해 먼저 알아보자.

우리가 로봇에게 전달하는 제어 신호는 robot frame 기준이지만, 도달하기 원하는 좌표를 world frame 상의 좌표이다. 따라서 homegeneous matrix가 계속해서 사용될 수밖에 없다. 예시를 통해 쉽게 이해해보자.

$(x =1, y = 1, \theta = 1/2)$인 로봇이 $(1, 0)$만큼 이동한다면 그 로봇의 state는 $(x=1, y=2, \theta=1/2)$가 됨을 우리는 직관적으로 알 수 있다.

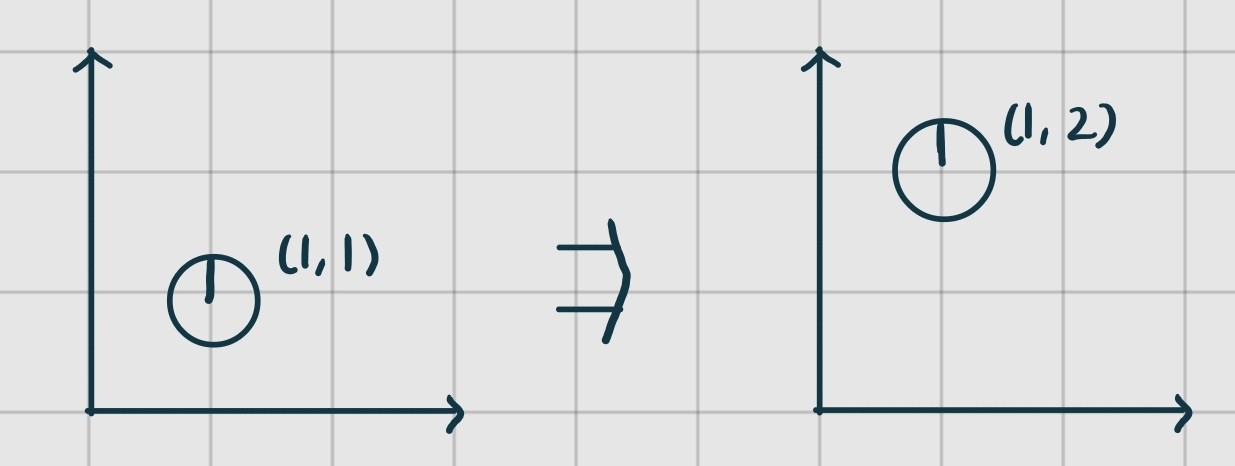
하지만 이를 homogeneous matrix를 사용하여 사용하여 나타낸다면 아래와 같다.

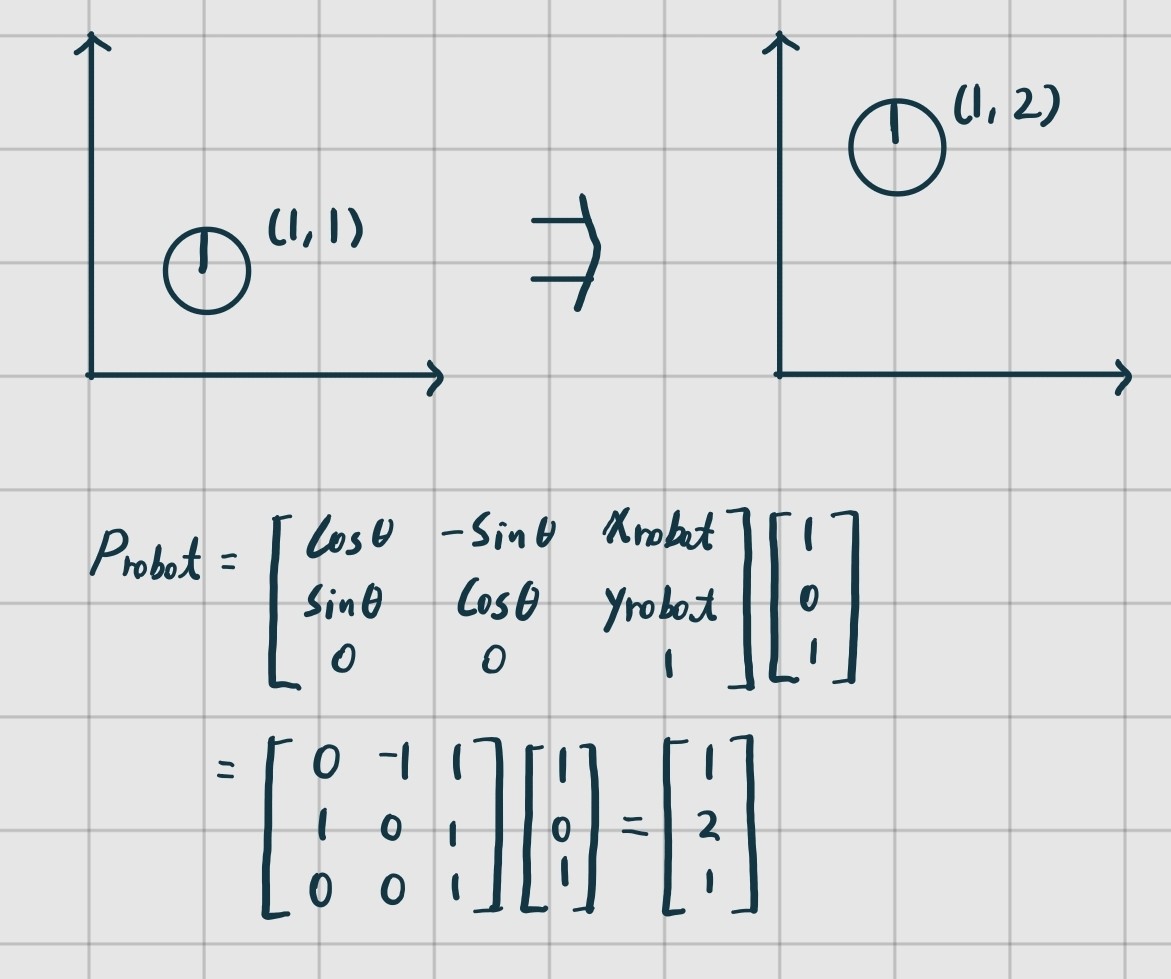
실제로 로봇을 제어할 때는 위와 같은 형식으로 homogeneous matrix를 누적해서 사용하게 된다.

3. Inverse Kinematics

먼저, inverse kinematics를 실행할 때 우리가 하고자 하는 바를 명확히 정의하자.

• Input: 현재 로봇의 state $(x, y, \theta)$와 로봇이 이동하기 원하는 $(x_{ref}, y_{ref})$.
• Output: 해당 $(x_{ref}, y_{ref})$로 움직이기 위한 제어 신호 $(v, \omega)$.

예시를 통해 inverse kinematics를 이해해보자.

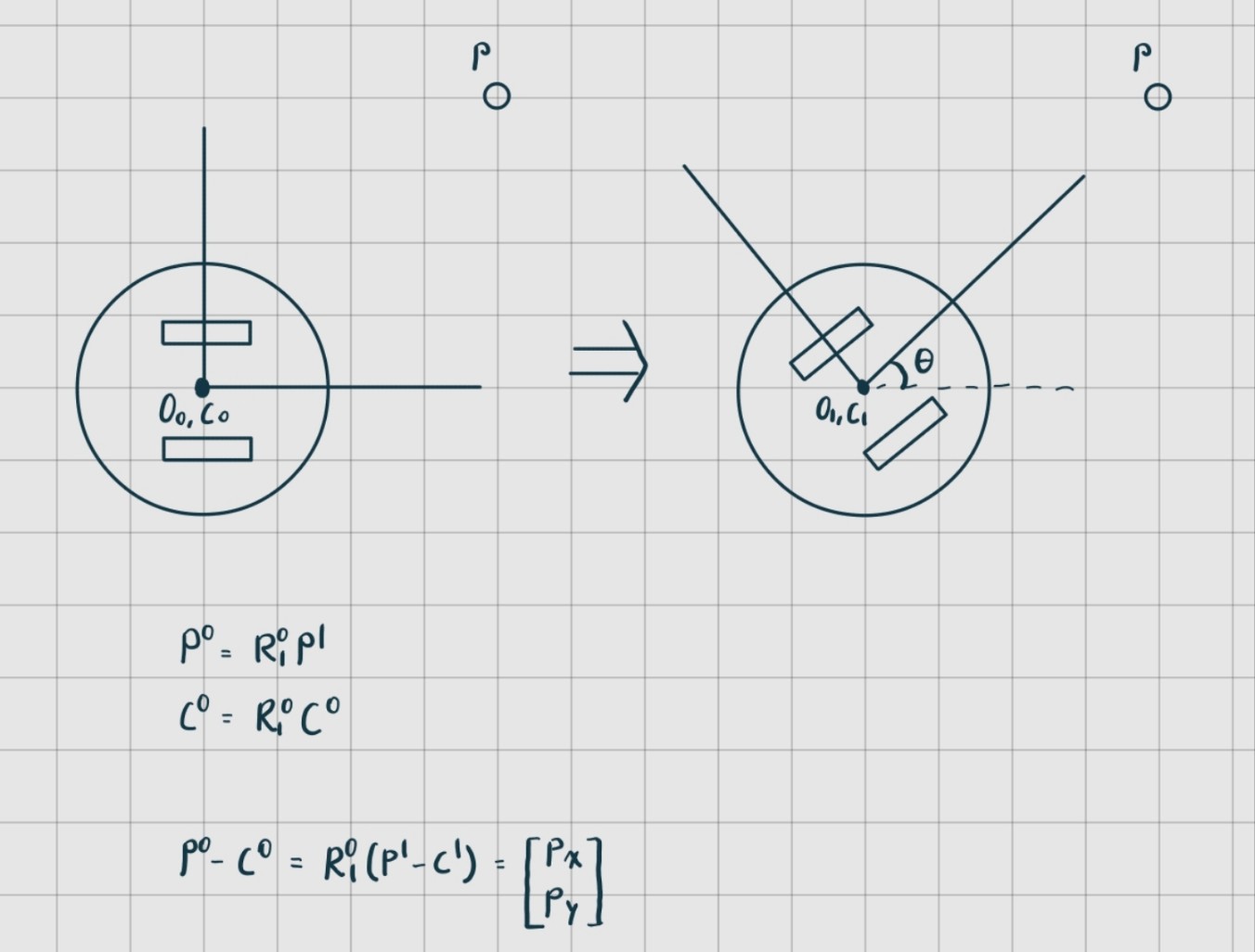
로봇의 중심점, 목표지점의 좌표는 $C_0, P_0$, 회전운동을 한 뒤의 이 두 점의 좌표는 $C_1, P_1$이다. $P^0 = R^0_1C^1$이고, $C^0=R^0_1C^1$이며 두식을 연립하면 $P^0-C^0=R^0_1(P^1-C^1)$의 식이 나오며 이 값을 로봇이 이동해야 하는 offset $\begin{bmatrix} P_x \\ P_y\end{bmatrix}$으로 설정한다.

그런뒤 해당 식을 전개한 뒤 시간에 대해 미분하면 아래와 같이 $P_x, P_y$와 $v, \omega$ 사이의 상관관계를 이끌어낼 수 있다.

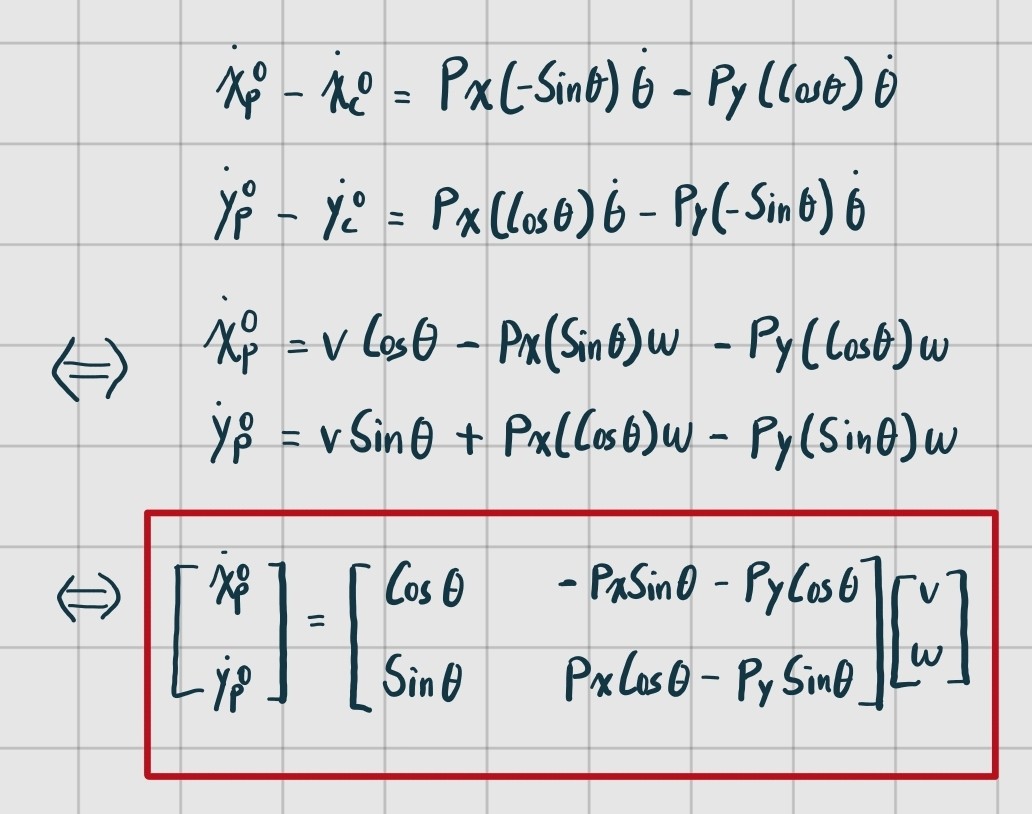
하지만 위 식에서 input은 $\begin{bmatrix} \dot{x^0_P} \\ \dot{y^0_P}\end{bmatrix}$이다. 즉 속도이다. 하지만 우리의 목적은 위치를 input으로 넣을 시 $v$와 $\omega$를 알아내는 것이었으므로, 추가적인 작업이 필요하다.

이를 위해 P Gain Controller를 사용해보도록한다. P gain controller에 대해서는 추후에 더 자세히 알아보도록한다.

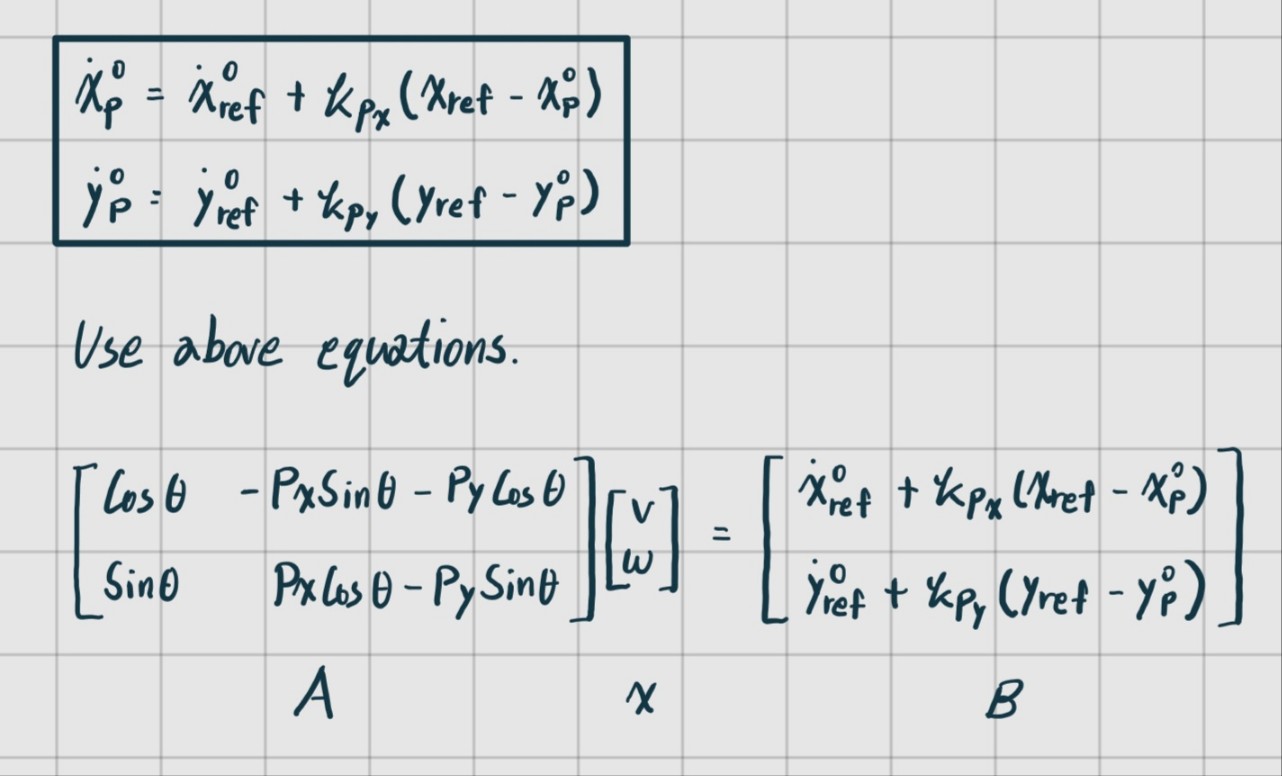
$\bm{Ax} = \bm{B}$의 꼴이 만들어졌다. $\bm{A}^{-1}$을 구하면 아래와같다.

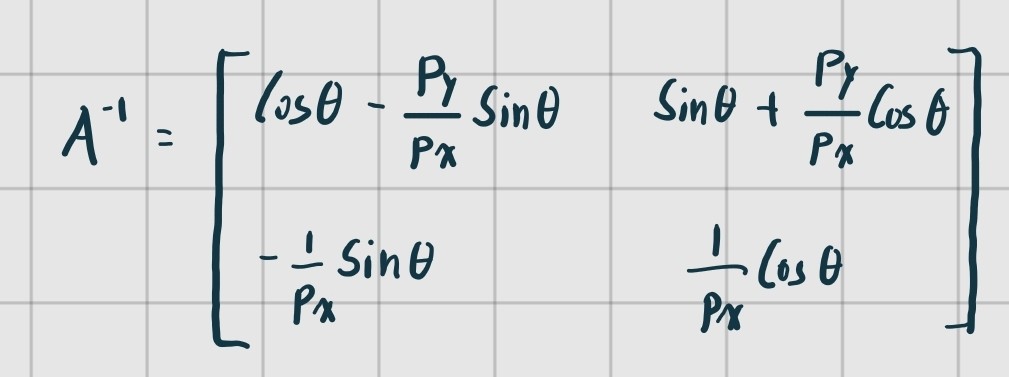
따라서 식을 $\bm{x}=\bm{A}^{-1}\bm{B}$의 형태로 변형할 수 있으며 위치와 $v, \omega$간의 관계가 완성되었다. 이 때 유의할 점은 아래와같다.

1. $P_x$가 0이 되면 안된다.
2. P gain $k_{P_{x}}$는 우리가 설정해야 하는 값으로 여러 시도를 통해 최적화한다.

---

Reference: 모두의 로보틱스 4강(DD mobile robot)(https://roadbalance.teachable.com/courses/5cee42/lectures/48650229)

질문, 조언 환영합니당 ■