Tensor

AAiss·2024년 8월 6일

AI Basics

목록 보기
2/12
post-thumbnail

서론

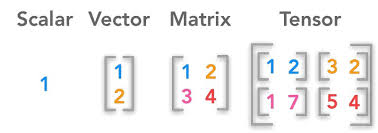
텐서(Tensor)는 배열(Array)이나 행렬(Matrix)과 매우 유사한 특수한 자료구조이다.

PyTorch에서는 텐서를 사용하여 모델의 입력과 출력뿐만 아니라 모델의 매개변수를 부호화(encode)한다.

Tensor

Tensor는 PyTorch의 핵심 데이터구조로서, NumPy의 다차원 배열과 유사한 형태로 데이터를 표현함

0-D Tensor

t = torch.tensor(36.5)
print('t =', t)

t = tensor(36.5000)

1-D Tensor

t = torch.tensor([175, 60, 81, 0.8, 0.9])
print('t =', t)

t = tensor([175.0000, 60.0000, 81.0000, 0.8000, 0.9000])

2-D Tensor

t = torch.tensor([[77, 114, 140, 191],
                  [39, 56, 46, 119],
                  [61, 29, 20, 33]])
print('t =', t)

t = tensor([[77, 114, 140, 191],
　　　　　[ 39, 56, 46, 119],
　　　　　[ 61, 29, 20, 33]])

3-D Tensor

t = torch.tensor([[[255, 0], [0, 255]],
				  [[0, 255], [0, 255]],
                  [[0, 0], [255, 0]]])
print('t =', t)

t = tensor([[[255, 0], [0, 255]],
　　　　　[[0, 255], [0, 255]],
　　　　　[[0, 0], [255, 0]]])

N-D Tensor

동일한 크기의 (N-1)-D Tensor들이 여러 개 쌓여 형성된 입체적인 배열 구조

데이터 타입

  • 정수형 데이터 타입
    • dtype = torch.uint8(8비트 부호 없는 정수)
    • dtype = torch.int8(8비트 부호 있는 정수)
    • dtype = torch.int16(16비트 부호 있는 정수)
    • dtype = torch.int32(32비트 부호 있는 정수)
    • dtype = torch.int64(64비트 부호 있는 정수)

  • 실수형 데이터 타입(부동 소수점)
    • dtype = torch.float32(32비트 부호 있는 실수)
    • dtype = torch.float64(64비트 부호 있는 실수)
t = torch.tensor(-1, dtype = torch.int8)
print('t =', t)
print('t.dtype =', t.dtype)

t = tensor(-1, dtype=torch.int8)
t.dtype = torch.int8

t = torch.tensor(1, dtype = torch.float32)
print('t =', t)
print('t.dtype =', t.dtype)

t = tensor(1.)
t.dtype = torch.float32

타입 캐스팅

Tensor의 타입을 변경할 수 있음

t = torch.tensor([2, 3, 4], dtype = torch.int8)
t_ = t.float()
print('t_.dtype =', t_.dtype)

t_.dtype = torch.float32

기초 메서드

  • min()
    • Tensor의 모든 요소들 중 최소값을 계산하는 함수

  • max()
    • Tensor의 모든 요소들 중 최대값을 계산하는 함수

  • sum()
    • Tensor의 모든 요소들의 합을 계산하는 함수

  • prod()
    • Tensor의 모든 요소들의 곱을 계산하는 함수

  • mean()
    • Tensor의 모든 요소들의 평균을 계산하는 함수

  • var()
    • ensor의 모든 요소들의 표본분산을 계산하는 함수

  • std()
    • Tensor의 모든 요소들의 표본표준편차를 계산하는 함수

t = torch.tensor([[1, 2, 3],
                  [3, 4, 5]], dtype = torch.float)

print('torch.min(t) =', torch.min(t))
print('torch.max(t) =', torch.max(t))
print('torch.sum(t) =', torch.sum(t))
print('torch.prod(t) =', torch.prod(t))
print('torch.mean(t) =', torch.mean(t))
print('torch.var(t) =', torch.var(t))
print('torch.std(t) =', torch.std(t))

torch.min(t) = tensor(1.)
torch.max(t) = tensor(5.)
torch.sum(t) = tensor(18.)
torch.prod(t) = tensor(360.)
torch.mean(t) = tensor(3.)
torch.var(t) = tensor(2.)
torch.std(t) = tensor(1.4142)

특성 메서드

  • dim()
    • Tensor의 차원의 수를 확인하는 함수

  • size()
    • Tensor의 모양(크기)를 확인하는 함수

  • shape()
    • Tensor의 모양(크기)를 확인하는 함수

  • numel()
    • Tensor의 요소의 총 개수를 확인하는 함수

t = torch.tensor([[1, 2, 3],
                  [3, 4, 5]], dtype = torch.float)

print('t.dim() =', t.dim())
print('t.size() =', t.size())
print('t.shape() =', t.shape())
print('t.numel() =', t.numel())

t.dim() = 2
t.size() = torch.Size([2, 3])
t.shape = torch.Size([2, 3])
t.numel() = 6

생성

특정 값으로 초기화된 Tensor

  • zeros()
    • 모든 요소들의 값이 0인 Tensor 생성

  • zeros_like(s)
    • s와 shape가 일치하며 모든 요소들의 값이 0인 Tensor 생성

  • ones()
    • 모든 요소들의 값이 1인 Tensor 생성

  • ones_like(s)
    • s와 shape가 일치하며 모든 요소들의 값이 1인 Tensor 생성
t = torch.zeros([2, 3])
print('t =', t)

t = tensor([[0., 0., 0.],
　　　　　[0., 0., 0.]])

t = torch.ones([3, 2])
print('t =', t)

t = tensor([[1., 1.],
　　　　　[1., 1.],
　　　　　[1., 1.]])

난수로 초기화된 Tensor

  • rand()
    • 연속균등분포 난수 값을 요소로 갖는 Tensor 생성

  • randn()
    • 표준정규분포 난수 값을 요소로 갖는 Tensor 생성
t = torch.rand([2, 3])
print('t =', t)

t = tensor([[0.4605, 0.0048, 0.3104],
　　　　　[0.9032, 0.9522, 0.2036]])

t = torch.randn([2, 3])
print('t =', t)

t = tensor([[ 0.7108, -0.3084, 0.5309],
　　　　　[ 0.0119, -0.7204, -0.9224]])

지정 범위 내 값으로 초기화된 Tensor

  • arange(start, end, step)
    • start 값부터 end 값 직전까지 step씩 더한 값을 요소로 갖는 Tensor 생성
    • Tensor의 요소 중 float 자료형이 포함된다면 t.dtype = float
    • Tensor의 요소 중 float 자료형이 포함되지 않는다면 t.dtype = int
t = torch.arange(start = 1, end = 11, step = 2)
# t = torch.arange(1, 11, 2)
print('t =', t)
print('t.dtype =', t.dtype)

t = tensor([1, 3, 5, 7, 9])
t.dtype = torch.int64

t = torch.arange(start = 1, end = 4, step = 0.5)
# t = torch.arange(1, 4, 0.5)
print('t =', t)
print('t.dtype =', t.dtype)

t = tensor([1.0000, 1.5000, 2.0000, 2.5000, 3.0000, 3.5000])
t.dtype = torch.float32

초기화되지 않은 Tensor

  • empty()
    • 초기화되지 않은 Tensor 생성

  • fill_()
    • 초기화 되지 않은 Tensor의 값 수정
    • 메모지 주소 변경 X
  • 성능 향상, 메모리 사용 최적화
    • Tensor 생성 후 곧바로 다른 값으로 덮어씌울 예정이라면 초기 값 설정이 불필요한 자원 소모임
t = torch.empty(5)
print('t =', t)

t = tensor([-1.5359e+10, 4.5846e-41, -1.5359e+10, 4.5846e-41, 4.4842e-44])

torch.fill_(t, 3.0)
print('t =', t)

t = tensor([3., 3., 3., 3., 3.])

t = torch.empty([2, 3])
print('t =', t)

t = tensor([[-1.5359e+10, 4.5846e-41, -1.3635e-17],
　　　　　[ 3.1361e-41, 4.4842e-44, 0.0000e+00]])

torch.fill_(t, 3.0)
print('t =', t)

t = tensor([[3., 3., 3.],
　　　　　[3., 3., 3.]])

list, Numpy 기반 Tensor

  • tensor()
    • list 기반 Tensor 생성

  • from_numpy()
    • Numpy 기반 Tensor 생성
s = [1, 2, 3, 4, 5, 6]
t = torch.tensor(s)
print('t =', t)

t = tensor([1, 2, 3, 4, 5, 6])

import numpy as np

s = np.array([[0, 1],
              [2, 3]])
t = torch.from_numpy(s)
print('t =', t)

t = tensor([[0, 1],
　　　　　[2, 3]])

CPU Tensor

  • IntTensor()
    • 정수형 CPU Tensor 생성

  • FloatTensor()
    • 실수형 CPU Tensor 생성
s = [1, 2, 3, 4, 5]
t = torch.IntTensor(s)
print('t =', t)

t = tensor([1, 2, 3, 4, 5], dtype=torch.int32)

import numpy as np

s = [1, 2, 3, 4, 5]
t = torch.FloatTensor(s)
print('t =', t)

t = tensor([1., 2., 3., 4., 5.])

CUDA Tensor

  • GPU(Graphics Processing Unit): 그래픽 처리 장치
    • 현재 AI 연구 및 개발에 있어 대규모 데이터 처리와 복잡한 계산에 사용
    • 병렬 처리 능력: GPU는 수천 개의 작은 코어를 가지고 있어 대량의 연산 동시 수행 가능
  • cuda.is_available()
    • GPU를 사용할 수 있는 환경인지 확인

  • cuda.get_device_name()
    • GPU 디바이스 이름 확인

  • cuda.device_count()
    • 사용 가능한 GPU 개수 확인

  • tensor.cuda()
    • Tensor를 GPU에 할당

  • tensor.cpu()
    • GPU에 할당된 Tensor를 CPU Tensor로 변환
t = torch.tensor([1, 2, 3])
print(t.device)

device(type='cpu')

print(torch.cuda.is_available())

True

print(torch.cuda.get_device_name(device=0))

'Tesla T4'

print(torch.cuda.device_count())

1

t = torch.tensor([1, 2, 3, 4, 5]).cuda()
# t = torch.tensor([1, 2, 3, 4, 5]).to(device = 'cuda')
print('t_gpu = ', t)

t_gpu = tensor([1, 2, 3, 4, 5], device='cuda:0')

t = torch.tensor([1, 2, 3, 4, 5]).cpu()
# t = torch.tensor([1, 2, 3, 4, 5]).to(device = 'cpu')
print('t_gpu = ', t)

t_cpu = tensor([1, 2, 3, 4, 5])

# 실제 사용 예시
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
t = t.to(device)

Shape 참조

  • zeros_like(s)
    • s와 shape가 동일하며 모든 요소들의 값이 0인 Tensor 생성

  • ones_like(s)
    • s와 shape가 동일하며 모든 요소들의 값이 1인 Tensor 생성

  • rand_like(s)
    • s와 shape가 동일하며 연속균등분포 난수 값을 요소로 갖는 Tensor 생성

  • randn_like(s)
    • s와 shape가 동일하며 표준정규분포 난수 값을 요소로 갖는 Tensor 생성
s = torch.ones([2, 3])
t = torch.zeros_like(s)
print('t =', t)

t = tensor([[0., 0., 0.],
　　　　　[0., 0., 0.]])

s = torch.zeros([2, 3])
t = torch.ones_like(s)
print('t =', t)

t = tensor([[1., 1., 1.],
　　　　　[1., 1., 1.]])

s = torch.zeros([2, 3])
t = torch.rand_like(s)
print('t =', t)

t = tensor([[0.6924, 0.1830, 0.2530],
　　　　　[0.4801, 0.5337, 0.7290]])

s = torch.zeros([2, 3])
t = torch.randn_like(s)
print('t =', t)

t = tensor([[-1.0576, 1.4039, 0.8849],
　　　　　[-0.7208, 0.3792, 0.4855]])

복제

  • clone()
    • Tensor 복제, 계산 그래프 분리 X

  • detach()
    • Tensor 복제, 계산 그래프 분리 O
s = torch.tensor([1, 2, 3, 4, 5, 6])
t = s.clone()
print('t =', t)

t = tensor([1, 2, 3, 4, 5, 6])

s = torch.tensor([1, 2, 3, 4, 5, 6])
t = s.detach()
print('t =', t)

t = tensor([1, 2, 3, 4, 5, 6])

인덱싱

  • Indexing
    • Tensor의 특정 요소에 접근
    • 음수 값도 Index로 사용 가능
t = torch.tensor([10, 20, 30, 40, 50, 60])
print('t[0] =', t[0])

t[0] = tensor(10)

t = torch.tensor([10, 20, 30, 40, 50, 60])
print('t[-2] =', t[-2])

t[-2] = tensor(50)

t = torch.tensor([[10, 20, 30],
                  [40, 50, 60]])
print('t[1, 2] = ', t[1, 2])
# print('t[1, 2] = ', t[1][2])

t[1, 2] = tensor(60)

슬라이싱

  • Slicing
    • 부분집합을 선택하여 sub Tensor 생성
    • 리스트의 Slicing과 유사
t = torch.tensor([10, 20, 30, 40, 50, 60])
print('t[1:4] =', t[1:4])

t[1:4] = tensor([20, 30, 40])

t = torch.tensor([[10, 20, 30],
                  [40, 50, 60]])
print('t[1, 2] = ', t[1, 2])

t[:, 1:] = tensor([[20, 30],
　　　　　　　[50, 60]])

차원 재구성

Shape 변경

  • view()
    • Tensor의 Shape 변경
    • Tensor의 요소들이 메모리에 연속적으로 할당된 경우 사용 가능
    • Tensor의 요소들은 기본적으로 메모리에 연속적으로 할당됨
    • Slicing 이후 Tensor의 요소들이 비연속적으로 할당될 수 있음
    • is_contiguous() 메서드를 통해 연속적인지 확인 가능
    • t = t.contiguous() 메서드를 통해 연속적으로 재할당 가능
    • N개의 차원 중 N - 1개 입력 시 나머지 하나의 차원에 해당하는 인자로 -1 사용 가능

  • reshape()
    • Tensor의 Shape 변경
    • Tensor의 요소들이 메모리에 비연속적으로 할당된 경우에도 사용 가능
    • 안전, 유연 But 성능 저하
s = torch.tensor([[0, 1, 2],
                  [3, 4, 5]])
t = s[:, :2]

if not t.is_contiguous():
	t = t.contiguous()
    print("Reallocation is done.")

t = t.view(1, -1)
print('t =', t)

Reallocation is done.
t = tensor([[0, 1, 3, 4]])

t = torch.arange(12)
t = t.reshape(2, -1)
print('t =', t)

t = tensor([[ 0, 1, 2, 3, 4, 5],
　　　　　[ 6, 7, 8, 9, 10, 11]])

평탄화

  • flatten(start_dim, end_dim)
    • start_dim 부터 end_dim까지 평탄화
    • end_dim 인자가 없다면 start_dim부터 tensor의 마지막 dim까지 평탄화
s = torch.zeros(3, 2, 2)
t = s.flatten(0)
print('t.shape =', t.shape)

t.shape = torch.Size([12])

s = torch.zeros(3, 2, 2)
t = s.flatten(1)
print('t.shape =', t.shape)

t.shape = torch.Size([3, 4])

s = torch.zeros(3, 2, 2)
t = s.flatten(2)
print('t.shape =', t.shape)

t.shape = torch.Size([3, 2, 2])

s = torch.zeros(3, 2, 2)
t = s.flatten(0, 1)
print('t.shape =', t.shape)

t.shape = torch.Size([6, 2])

Transpose

  • transpose(dim_1, dim_2)
    • dim_1 과 dim_2 전치
s = torch.tensor([[0, 1, 2],
                 [3, 4, 5]])
t = s.transpose(0, 1)
print('t =', t)

t = tensor([[0, 3],
　　　　　[1, 4],
　　　　　[2, 5]])

s = torch.tensor([[[0, 1],
                  [2, 3],
                  [4, 5]],

                 [[6, 7],
                  [8, 9],
                  [10, 11]],

                 [[12, 13],
                  [14, 15],
                  [16, 17]]])
t = s.transpose(1, 2)
print('t =', t)

t = tensor([[[ 0, 2, 4], [ 1, 3, 5]],
　　　　　[[ 6, 8, 10], [ 7, 9, 11]],
　　　　　[[12, 14, 16], [13, 15, 17]]])

차원 축소

  • squeeze()
    • dim이 1인 차원 삭제
    • square bracket('[', ']')을 삭제할 수 있는 경우 squeeze()함수로 삭제한다 생각
s = torch.zeros(1, 3, 4)
t = s.squeeze()
print('s =', s, '\n')
print('t =', t, '\n')
print('t.shape =', t.shape)

s = tensor([[[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.]]])

t = tensor([[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.]])

t.shape = torch.Size([3, 4])

차원 확장

  • unsqueeze(dim)
    • dim 차원 추가
    • square bracket('[', ']')을 unsqueeze()함수로 추가한다 생각
s = torch.zeros(3, 4)
t = s.unsqueeze(dim=1)
print('s =', s, '\n')
print('t =', t, '\n')
print('t.shape =', t.shape)

s = tensor([[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.],
　　　　　[0., 0., 0., 0.]])

t = tensor([[[0., 0., 0., 0.]],
　　　　　[[0., 0., 0., 0.]],
　　　　　[[0., 0., 0., 0.]]])

t.shape = torch.Size([3, 1, 4])

결합

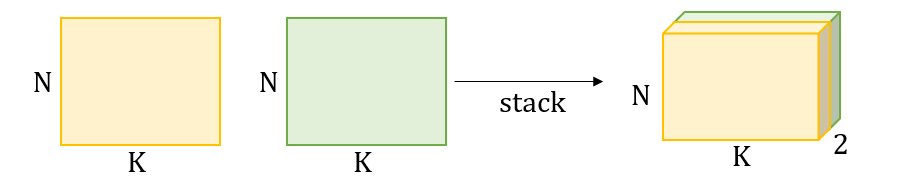
  • stack(tuple, dim)
    • 여러 tensor를 dim 방향으로 쌓여 새로운 tensor 생성
    • 새로운 차원이 생성
    • tensor들을 tuple 형식으로 묶어 인자로 넘겨야 함
    • dim 값이 없다면 dim = 0
  • cat(tuple, dim)
    • 여러 tensor를 dim 방향으로 연결하여 새로운 tensor 생성
    • 기존 차원이 유지
    • tensor들을 tuple 형식으로 묶어 인자로 넘겨야 함
    • dim 값이 없다면 dim = 0
    • dim 기준 shape 값이 일치하지 않는다면 에러 발생
출처: https://sanghyu.tistory.com/85 
red_channel = torch.tensor([[255, 0],
                            [0, 255]])
green_channel = torch.tensor([[0, 255],
                              [0, 255]])
blue_channel = torch.tensor([[0, 0],
                             [255, 0]])

t = torch.stack((red_channel, green_channel, blue_channel), dim = 0)
print('t =', t)
print('t.shape = ', t.shape)

t = tensor([[[255, 0],
　　　　　[0, 255]],
　　　　　[[ 0, 255],
　　　　　[0, 255]],
　　　　　[[0, 0],
　　　　　[255, 0]]])

t.shape = torch.Size([3, 2, 2])

u = torch.tensor([[0, 1],
                  [2, 3]])
v = torch.tensor([[4, 5]])
t = torch.cat((u, v))
print('t =', t)
print('t.shape =', t.shape)

t = tensor([[0, 1],
　　　　　[2, 3],
　　　　　[4, 5]])

t.shape = torch.Size([3, 2])

u = torch.tensor([[0, 1],
                  [2, 3]])
v = torch.tensor([[4, 5]])
t = torch.cat((u, v), dim=1)
print('t =', t)
print('t.shape =', t.shape)

Error

u = torch.tensor([[0, 1],
                  [2, 3]])
v = torch.tensor([[4, 5]])
t = torch.cat((u, v.view(2, 1)), dim=1)
print('t =', t)
print('t.shape =', t.shape)

t = tensor([[0, 1, 4],
　　　　　[2, 3, 5]])

t.shape = torch.Size([2, 3])

크기 확장

  • expand(dim_1_size, dim_2_size)
    • 크기가 1인 차원의 크기 확장
    • shape: (dim_1_size * dim_2_size)
    • 크기가 1인 차원이 존재해야 사용 가능

  • repeat(dim_1_times, dim_2_times)
    • 차원의 크기 확장
    • shape: ((dim_1_size * dim_1_times) * (dim_2_size * dim_2_times))
t = torch.tensor([[1, 2, 3]])
t = t.expand(4, 3)

print('t =', t)
print('t.shape =', t.shape)

t = tensor([[1, 2, 3],
　　　　　[1, 2, 3],
　　　　　[1, 2, 3],
　　　　　[1, 2, 3]])

t.shape = torch.Size([4, 3])

t = torch. tensor([[1, 2],
                   [3, 4]])
t = t.repeat(2, 3)
print('t =', t)
print('t.shape =', t.shape)

t = tensor([[1, 2, 1, 2, 1, 2],
　　　　　[3, 4, 3, 4, 3, 4],
　　　　　[1, 2, 1, 2, 1, 2],
　　　　　[3, 4, 3, 4, 3, 4]])

t.shape = torch.Size([4, 6])

기초 연산

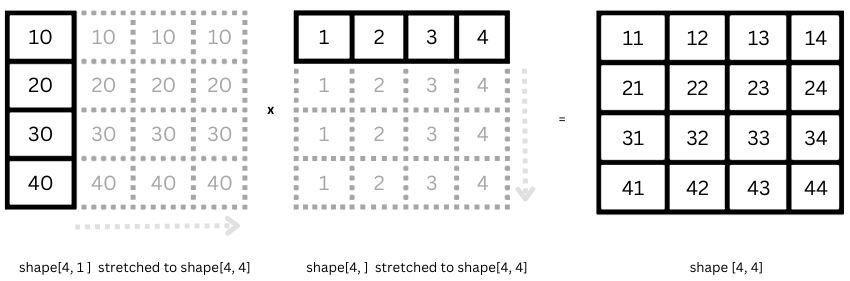
BroadCasting

Tensor 연산 시 shape가 일치하지 않는다면 연산이 가능하도록 각 Tensor를 확장

출처: https://www.machinelearningnuggets.com/tensorflow-tensors-what-are-tensors-understanding-the-basics-creating-and-working-with-tensors/

Inplace 방식

  • 추가적인 메모리 할당 없이 tensor_1에 연산 결과를 덮어 씌움
  • Autograd와의 호환성 측면에서 문제를 일으킬 수 있음
u = torch.tensor([[1, 2],
                  [3, 4]])
v = torch.tensor([[1, 3],
                  [5, 7]])

print('u+v =', u.add_(v))

u+v = tensor([[ 2, 5],
　　　　　　[8, 11]])

산술 연산

  • add(tensor_1, tensor_2)
    • tensor의 덧셈

  • sub(tensor_1, tensor_2)
    • tensor의 뺄셈

  • mul(tensor_1, tensor_2)
    • tensor의 곱셈

  • div(tensor_1, tensor_2)
    • tensor의 나눗셈

  • pow(tensor, scalar)
    • tensor의 거듭제곱
    • pow(t, n): t의 n 거듭제곱
    • pow(t, 1/n): t의 n 거듭제곱근
u = torch.tensor([[1, 2],
                  [4, 5]])
v = torch.tensor([1, 3])
print('u+v =', torch.add(u, v))

u+v = tensor([[2, 5],
　　　　　　[5, 8]])

u = torch.tensor([[1, 2],
                  [4, 5]])
v = torch.tensor([1, 3])
print('u+v =', torch.sub(u, v))

u+v = tensor([[0, -1],
　　　　　　[3, 2]])

u = torch.tensor([[1, 2],
                  [4, 5]])
v = torch.tensor([1, 3])
print('u+v =', torch.mul(u, v))

u+v = tensor([[1, 6],
　　　　　　[4, 15]])

u = torch.tensor([[18, 9],
                  [10, 4]])
v = torch.tensor([[6, 3],
                  [5, 2]])
print('u+v =', torch.div(u, v))

u+v = tensor([[3., 3.],
　　　　　　[2., 2.]])

t = torch.tensor([[1, 2],
                  [3, 4]])
print('t^2 =', torch.pow(t, 2))
print('t^3 =', torch.pow(t, 3))

t^2 = tensor([[ 1, 4],
　　　　　　[ 9, 16]])

t^3 = tensor([[ 1, 8],
　　　　　　[27, 64]])

비교 연산

  • eq(tensor_1, tensor_2)
    • equal to
    • result[i] = (tensor_1[i] == tensor_2[i])

  • ne(tensor_1, tensor_2)
    • not equal to
    • result[i] = (tensor_1[i] != tensor_2[i])

  • gt(tensor_1, tensor_2)
    • greater than
    • result[i] = (tensor_1[i] > tensor_2[i])

  • ge(tensor_1, tensor_2)
    • greater than or eqaul to
    • result[i] = (tensor_1[i] >= tensor_2[i])

  • lt(tensor_1, tensor_2)
    • less than
    • result[i] = (tensor_1[i] < tensor_2[i])

  • le(tensor_1, tensor_2)
    • less than or eqaul to
    • result[i] = (tensor_1[i] <= tensor_2[i])
u = torch.tensor([1, 3, 5, 7])
v = torch.tensor([2, 3, 5, 7])
print('u == v :', torch.eq(u, v))
print('u != v :', torch.ne(u, v))
print('u > v :', torch.gt(u, v))
print('u >= v :', torch.ge(u, v))
print('u < v :', torch.lt(u, v))
print('u <= v :', torch.le(u, v))

u == v : tensor([False, True, True, True])
u != v : tensor([ True, False, False, False])
u > v : tensor([False, False, False, False])
u >= v : tensor([False, True, True, True])
u < v : tensor([ True, False, False, False])
u <= v : tensor([True, True, True, True])

논리 연산

  • logical_and(tensor_1, tensor_2)
    • result[i] = (tensor_1[i] and tensor_2[i])

  • logical_or(tensor_1, tensor_2)
    • result[i] = (tensor_1[i] or tensor_2[i])

  • logical_xor(tensor_1, tensor_2)
    • result[i] = (tensor_1[i] xor tensor_2[i])
u = torch.tensor([True, True, False, False])
v = torch.tensor([True, False, True, False])
print('and(u, v) =', torch.logical_and(u, v))
print('or(u, v) =', torch.logical_or(u, v))
print('xor(u, v) =', torch.logical_xor(u, v))

and(u, v) = tensor([ True, False, False, False])
or(u, v) = tensor([ True, True, True, False])
xor(u, v) = tensor([False, True, True, False])

Norm

Norm(Lp):　∥x∥p=(∑i=1n∣xi∣p)1/p(p≥1)Norm(L_p):　 \begin{Vmatrix} x \end{Vmatrix}_p \displaystyle= \left(\sum_{i=1}^{n}|x_i|^p\right)^{1/p} (p\ge1)

L1 Norm (맨해튼 Norm)

x=[x1,x2],　∥x∥1=∣x1∣+∣x2∣x = [x_1, x_2],　\begin{Vmatrix} x \end{Vmatrix}_1\displaystyle= |x_1| + |x_2|

t = torch.tensor([4, 3], dtype=torch.float32)
L1_norm = torch.norm(t, p=1)
print(f'L1 Norm of a: {L1_norm}')

L1 Norm of a: 7.0

L2 Norm (유클리드 Norm)

x=[x1,x2],　∥x∥2=∣x1∣2+∣x2∣2x = [x_1, x_2],　\begin{Vmatrix} x \end{Vmatrix}_2\displaystyle= \sqrt{|x_1|^2 + |x_2|^2}

t = torch.tensor([4, 3], dtype=torch.float32)
L2_norm = torch.norm(t, p=2)
print(f'L2 Norm of a: {L2_norm}')

L2 Norm of a: 5.0

유사도

두 1-D Tensor가 얼마나 유사한지에 대한 측정값

맨해튼 유사도

Manhattan Distance=∑i=1n∣xi−yi∣Manhattan\ Distance\displaystyle= \sum_{i=1}^{n}|x_i - y_i|

Mahattan Similarity=1/(1+Mahattan Distance)\\Mahattan\ Similarity\displaystyle= 1/(1 + Mahattan\ Distance)

u = torch.tensor([1, 0, 2], dtype=torch.float32)
v = torch.tensor([0, 1, 2], dtype=torch.float32)

manhattan_distance = torch.norm(u - v, p = 1)
manhattan_similarity = 1 / (1 + manhattan_distance)

print(f'Manhattan Distance: {manhattan_distance}')
print(f'Manhattan Similarity: {manhattan_similarity}')

Manhattan Distance: 2.0
Manhattan Similarity: 0.3333333432674408

유클리드 유사도

Euclidean Distance=∑i=1n∣xi−yi∣2Euclidean\ Distance\displaystyle= \sqrt{\sum_{i=1}^{n}{|x_i - y_i|}^2}

Euclidean Similarity=1/(1+Euclidean Distance)\\Euclidean\ Similarity\displaystyle= 1/(1 + Euclidean\ Distance)

u = torch.tensor([1, 0, 2], dtype=torch.float32)
v = torch.tensor([0, 1, 2], dtype=torch.float32)

euclidean_distance = torch.norm(u - v, p = 2)
euclidean_similarity = 1 / (1 + euclidean_distance)

print(f'Euclidean Distance: {euclidean_distance}')
print(f'Euclidean Similarity: {euclidean_similarity}')

Euclidean Distance: 1.4142135381698608
Euclidean Similarity: 0.41421353816986084

코사인 유사도

cos(x,y)=<x,y>∥x∥2∥y∥2cos(x, y)\displaystyle= \frac{<x, y>}{\begin{Vmatrix}x\end{Vmatrix}_2\begin{Vmatrix}y\end{Vmatrix}_2}

u = torch.tensor([1, 0, 2], dtype=torch.float32)
v = torch.tensor([0, 1, 2], dtype=torch.float32)

dot_product = torch.dot(u, v)
cosine_similarity = torch.dot(u, v) / (torch.norm(u, p = 2) * torch.norm(v, p = 2))

print(f'Cosine Similarity: {cosine_similarity}')

Cosine Similarity: 0.800000011920929

2-D 곱셈 연산

  • matmul(tensor_1, tensor_2)
    • mm(tensor_1, tensor_2) 혹은 tensor_1 @ tensor_2로 대체 가능 
u = torch.tensor([[1, 1, 3],
                  [4, 5, 6],
                  [7, 8, 9]])
v = torch.tensor([[1, 0],
                  [1, -1],
                  [2, 1]])

t = torch.matmul(u, v)
# t = torch.mm(u, v)
# t = u @ v
print('t =', t)

t = tensor([[ 8, 2],
　　　　　[21, 1],
　　　　　[33, 1]])

대칭

  • flip(tensor, list)
    • tensor를 list 내의 dim 기준으로 대칭
t = torch.tensor([[[1, 2, 3],
                  [4, 5, 6]],
                  [[3, 2, 4],
                   [5, 2, 1]]])
symmetric_t = torch.flip(t, [0])
print('symmetric_t =',symmetric_t)

symmetric_t = tensor([[[3, 2, 4],
　　　　　　　　　　[5, 2, 1]],
　　　　　　　　　　[[1, 2, 3],
　　　　　　　　　　[4, 5, 6]]])

t = torch.tensor([[[1, 2, 3],
                  [4, 5, 6]],
                  [[3, 2, 4],
                   [5, 2, 1]]])
symmetric_t = torch.flip(t, [1])
print('symmetric_t =',symmetric_t)

symmetric_t = tensor([[[4, 5, 6],
　　　　　　　　　　[1, 2, 3]],
　　　　　　　　　　[[5, 2, 1],
　　　　　　　　　　[3, 2, 4]]])

t = torch.tensor([[[1, 2, 3],
                  [4, 5, 6]],
                  [[3, 2, 4],
                   [5, 2, 1]]])
symmetric_t = torch.flip(t, [0, 1])
print('symmetric_t =',symmetric_t)

symmetric_t = tensor([[[5, 2, 1],
　　　　　　　　　　[3, 2, 4]],
　　　　　　　　　　[[4, 5, 6],
　　　　　　　　　　[1, 2, 3]]])

결론

PyTorch의 Tensor는 딥러닝과 머신러닝에서 데이터 처리를 위한 필수적인 도구이다.

다양한 차원에서의 표현과 강력한 연산 기능을 통해, 연구자와 개발자들은 복잡한 모델을 쉽게 구현하고 학습시킬 수 있다.

Tensor는 단순한 데이터 구조 이상의 의미를 가지며, GPU 가속을 통한 고속 연산과 자동 미분 기능으로 신경망 학습의 효율성을 높여준다.

본 글에서 설명한 다양한 Tensor의 유형과 연산, 초기화 방법, 데이터 타입 변환 및 변형 기법들은 PyTorch를 활용하는 데 있어 기초적인 이해를 돕는다.

이를 통해 사용자는 자신만의 모델을 설계하고 최적화하며, 더 나아가 데이터 과학 및 인공지능 분야의 다양한 문제를 해결할 수 있는 능력을 갖추게 된다.

profile
AAiss
.
이전 포스트

Pytorch

다음 포스트

Machine Learning

0개의 댓글