Regression

AAiss·2024년 8월 12일

AI Basics

목록 보기

8/12

서론

회귀분석(Regression Analysis)은 통계학 및 머신러닝에서 중요한 기법 중 하나로, 변수 간의 관계를 모델링하고 예측하는 데 사용된다.

특히, 회귀분석은 주어진 데이터를 기반으로 연속적인 결과 변수를 예측하는 데 유용하다.

본 포스팅에서는 회귀분석의 기본 개념과 다양한 유형, 특히 선형 회귀(Linear Regression)에 대해 설명하고, 손실 함수 및 성능 평가 지표를 통해 모델의 정확성을 평가하는 방법을 다룰 것이다.

회귀분석(Regression Analysis)

관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정

변수: 값이 변하는 데이터 요소 또는 속성

독립변수(설명변수): 결과의 원인( $x$ )

종속변수(응답변수): 독립변수에 따라 값이 달라짐( $y$ )

Linear Regression

종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하는 통계적 방법

독립 변수의 값을 기반으로 종속 변수의 값을 예측

$y = mx + b$

$x$ : 독립 변수 (예측 변수)

$y$ : 종속 변수 (목표)

$m$ : 직선의 기울기 (회귀 계수)

$b$ : $y$ 절편 (상수항)

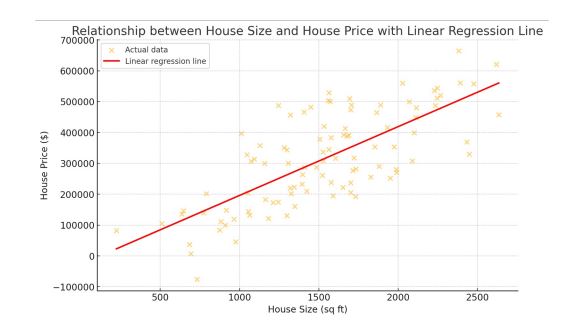
집값과 집 크기 간의 상관관계를 나타낸 산점도

$x$ 축: 집 크기

$y$ 축: 집 값

모델 평가 지표

MAE (평균 절대 오차)

$MAE = \displaystyle\frac{1}{n}\sum_{i = 1}^{n}|y_i - \hat{y_i}|$

예측 값이 실제 값과 얼마나 차이나는지를 절대값으로 계산해 평균화한 지표

모든 오차를 동일하게 고려하므로 해석이 간단하고, 단위가 종속 변수와 동일

주로 일상적인 예측 성능 평가, 쉽게 해석 가능한 경우 사용

MSE (평균 제곱 오차)

$MSE = \displaystyle\frac{1}{n}\sum_{i = 1}^{n}(y_i - \hat{y_i})^2$

실제 값과 예측 값 간의 차이의 제곱을 평균낸 값

오차를 제곱하므로 큰 오차에 더 큰 패널티를 부여

큰 오차에 민감하게 반응하므로, 모델의 큰 오차를 줄이는 데 유용

단위가 제곱된 형태라 실제 값과 다를 수 있음

주로 모델의 큰 오차를 중요하게 다루어야 하는 경우 사용

RMSE (제곱근 평균 제곱 오차)

$RMSE = \displaystyle\sqrt{\frac{1}{n}\sum_{i = 1}^{n}(y_i - \hat{y_i})^2}$

MSE에 제곱근을 취한 값으로, 오차를 원래 단위로 변환

MSE와 같은 장점을 가지면서도 단위 문제를 해결

해석이 용이하고, 큰 오차에 민감하게 반응하는 동시에 실제 값과 같은 단위를 유지

R² (결정 계수)

$R^2 = \displaystyle1 - \frac{\sum_{i = 1}^{n}(y_i - \hat{y_i})^2}{\sum_{i = 1}^{n}(y_i - \bar{y_i})^2}$

모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타내는 지표

0에서 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 잘 설명하는 것

비교적 해석이 쉽고 다른 모델과 비교할 때 유용

주로 모델의 설명력을 평가할 때, 특히 여러 모델의 성능을 비교할 경우 사용