Classification

서론

Classifier(분류기)는 주어진 데이터를 기반으로 특정 클래스에 속하는지를 판단하는 알고리즘으로, 머신러닝에서 중요한 역할을 한다.

다양한 분류 알고리즘이 존재하지만, 각기 다른 특성과 장점을 가지고 있어 특정 문제에 적합한 방법을 선택하는 것이 중요하다.

본 포스팅에서는 KNN Classifier, Linear Classifier, Softmax Classifier 등 다양한 분류 방법을 소개하고, KNN Classifier의 단점과 Linear Classifier와 Softmax Classifier를 결합하여 사용하는 이유를 설명할 것이다.

---

KNN Classifier

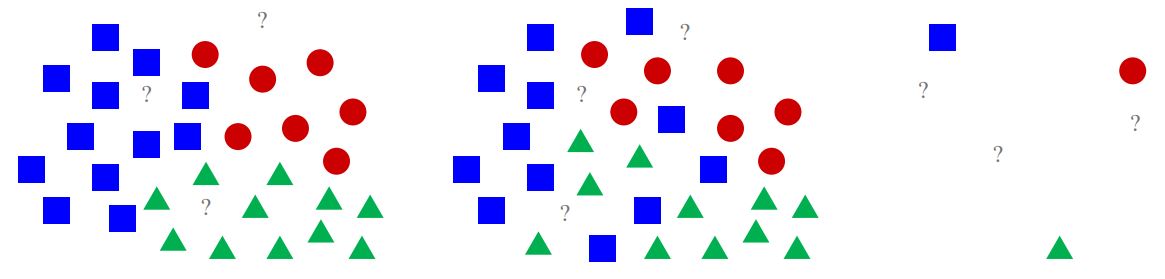
테스트 데이터 포인트에 대해 가장 가까운 학습 데이터 포인트를 $k$개 찾고, 레이블을 사용하여 예측

def train(images, labels):  # 모든 데이터와 레이블 기억
# some machine learning
return model

def predict(model, image):  # 가장 유사한 훈련 예제의 레이블 출력
# use the model
return predicted_label

• 학습은 한번, 예측은 여러번 진행됨
• 예측 과정에서 모든 데이터와 레이블을 확인: $O(N)$ Time 😥

---

Linear Classifier

모든 훈련 예제를 외우는 대신 입력(이미지 $x$)을 레이블 점수(클래스 $y$)에 매핑

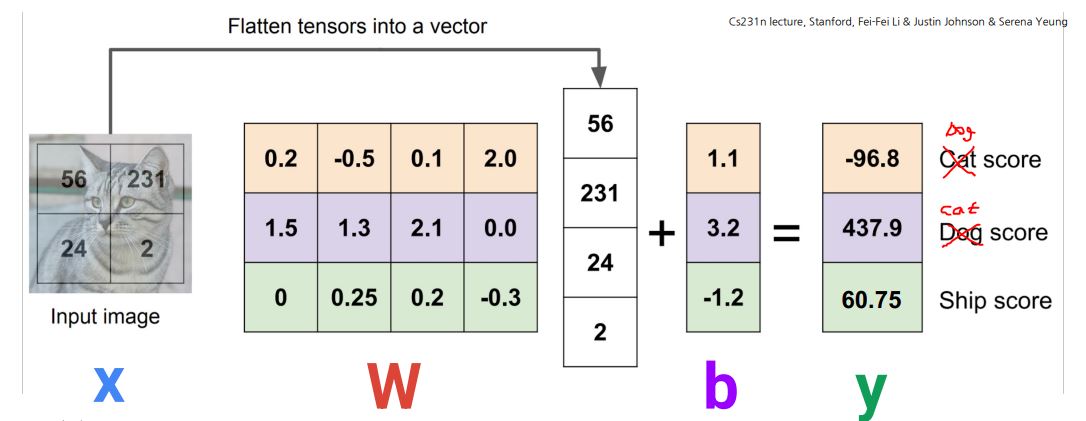
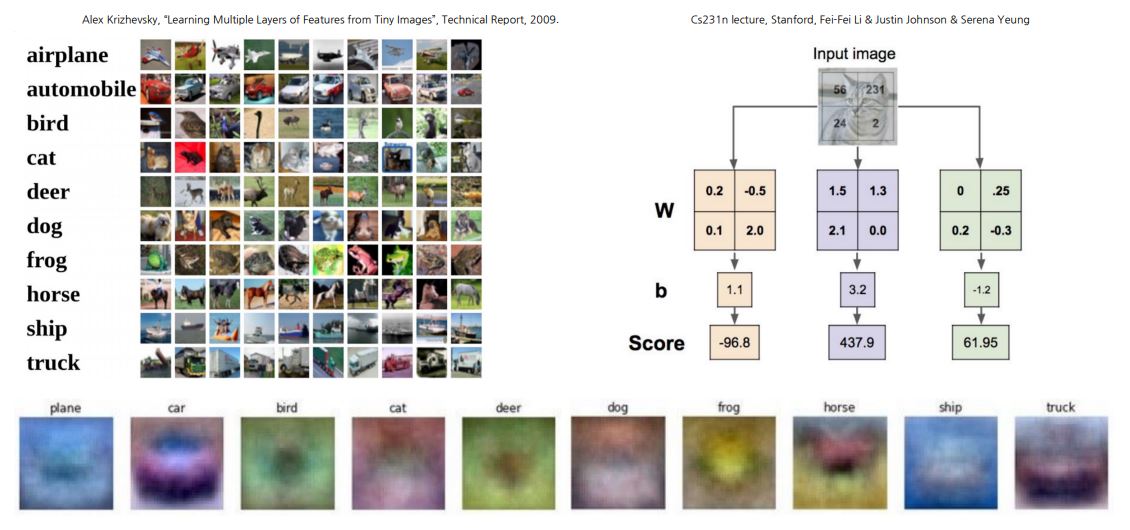
• 학습 시: 트레이닝 데이터에서 템플릿 학습
• 테스트 시: 새로운 예제로 템플릿 매칭
  
  
• KNN
  • N: 학습 데이터의 개수
  • O(N) Time 😥
• Linear
  • M: 클래스의 개수 😀
  • O(M) Time
    
    
• 일반적으로 M << N

---

Softmax Classifier

• Linear Classifier의 Score는 제한이 없으므로 해석에 어려움이 있음
• Score를 각 클래스에 속할 확률로 변환

각 클래스에 속할 확률

• 2개의 클래스가 있다 가정
• $s_1 > s_2$라면 $c_2$보다 $c_1$에 속할 확률이 더 높음
• 클래스 간 갭($s_1 - s_2)$이 더 클수록, $x ⋲ c_1$일 확률이 더 높음

---

Sigmoid 함수

• $s = s_1 - s_2$
• $s$(양수)의 값이 클수록 1에 가까운 값을 반환
• $s$(음수)의 절대값이 클수록 0에 가까운 값을 반환
• $s$의 값이 0이면 0.5를 반환

$p(y =c_1|x) = \displaystyle\frac{1}{1 + e^{-(s_1 - s_2)}}$

$p(y =c_2|x) = \displaystyle\frac{1}{1 + e^{-(s_2 - s_1)}}$

---

Softmax 함수

Sigmoid함수의 일반화

$p(y =c_i|x) = \displaystyle\frac{e^{s_i}}{\sum_{j = 1}^{n}{e^{s_j}}}$

---

손실 함수

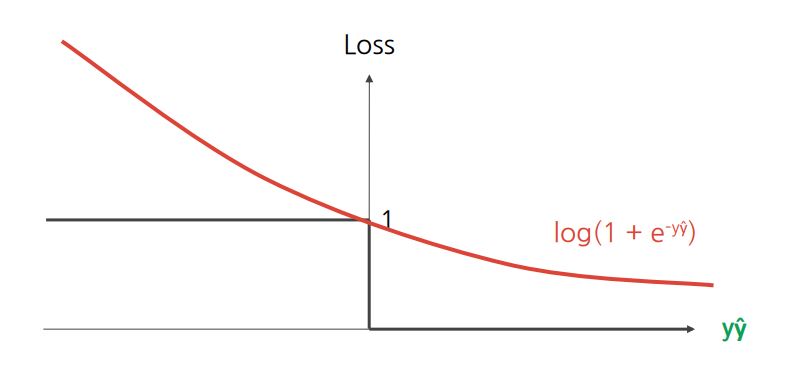
로그 손실

예측이 정확할수록 페널티 감소

---

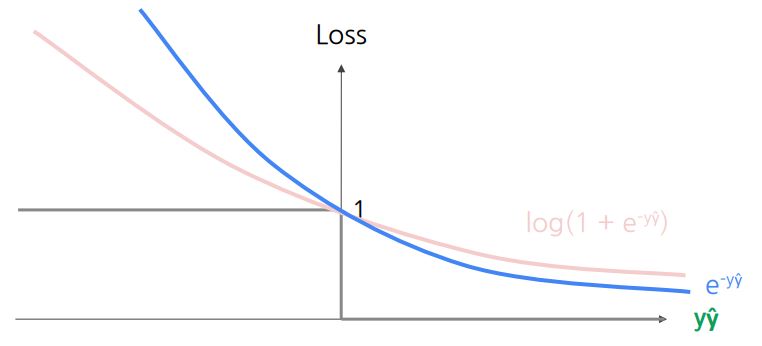
지수 손실

• 로그 손실과 유사
• 잘못된 경우 더 높은 패널티, 올바른 경우 더 낮은 패널티

---

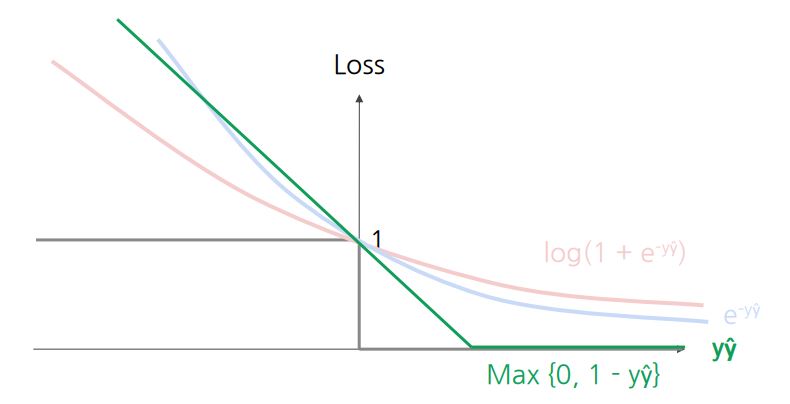
힌지 손실 (SVM)

• 오류에 대한 패널티가 선형적으로 증가
• 오차 범위 내에서 정답인 경우에도 약간의 패널티 적용

---

교차 엔트로피 (Cross Entropy)

집합에서 추출한 이벤트를 식별하는 데 필요한 평균 비트 수를 측정

---

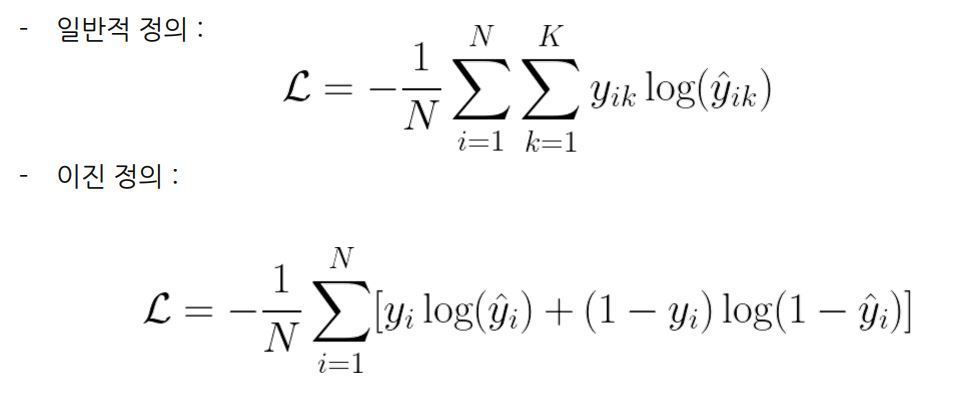
결론

본 포스팅에서는 다양한 분류 기법과 그 작동 원리를 살펴보았다.

KNN Classifier, Linear Classifier, Softmax Classifier에 대해 학습하였고, KNN Classifier의 단점과 Linear Classifier와 Softmax Classifier를 결합하여 사용하는 이유를 살펴보았다.

또한, Sigmoid 및 Softmax 함수와 손실 함수는 모델의 성능을 평가하고 개선하는 데 필수적인 요소이다.

---