딥러닝에서 미분값의 사용
딥러닝에서 미분값의 사용은 정확히는 손실함수의 특정변수에 대한 미분값이 사용된다. 손실함수는 정답과 예측값의 차이를 대변해주는 것이다. 정답은 고정되어 상수이지만, 예측값의 경우 여러 가중치와 입력값 그리고 활성화 함수의 조합이다.
우리가 업데이트, 즉 학습과정에서 수정이 필요한 변수는 가중치이다. 가중치는 입력값에 곱해지고 더해진다.(입력값 x weight + bias : 아핀변환) 그리고나서 활성화 함수라는 비선형 함수의 입력으로 들어간다. 활성화 함수를 통해 나온 결괏값은 다시 다음 레이어의 입력으로 투입된다. 같은 현상의 반복이다.
예시로 두개의 활성화 함수를 엮어본다면 다음과 같은 수식으로 적을 수 있다.
= 활성화함수1(활성화함수2(wx+b) x w + b)
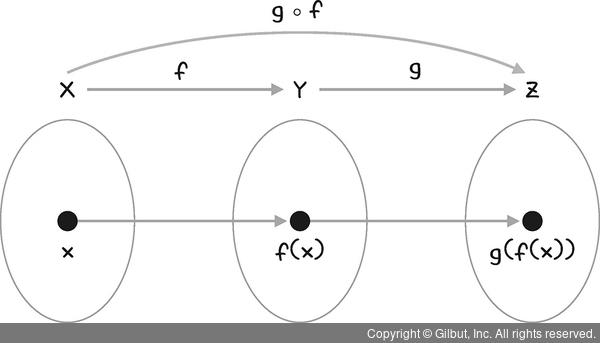
즉 이 구조는 합성함수의 성질을 띄고 있으며, 이런 방식으로 더 많이 반복되더라도 합성함수안에 합성함수가 존재하는 꼴이 된다. 이렇게 계산된 합성함수의 결괏값은 예측값이 된다.(특정 수식을 통해 우리가 의도한 값) 예측값과 정답의 차이를 나타내주는 함수가 바로 손실함수(Loss function)이다.
= 손실함수(인자1 = 정답, 인자2=활성화함수1(활성화함수2(wx+b) x w + b))
중요한 것은 이렇게 의미를 더해도 결국 수식적으로는 다시 합성함수꼴이라는 것이다. 딥러닝에서는 이 손실함수의 미분값이 사용되는 것이다.
미분의 뜻
미분의 뜻은 아주 작은 움직임에 대한 연관된 움직임의 파악이다. 즉 미분은 주어진 관계식에 변수들이 존재할 때 어떤 변수의 움직임에 대한 다른 변수의 움직임이다. 그런데 그 움직임은 매우 작아 0에 수렴하는 움직임이다. 이것이 전부이다.
dLoss/dw1 의 뜻은 w1에 대한 Loss의 미분값이다. 풀어서 설명하면 w1이 매우 작게 움직인다면, dLoss는 얼마나 움직이나에 대한 값인 것이다.
딥러닝 손실함수속에는 단순히 두개의 변수만 존재하지 않는다. 수많은 가중치 변수들이 존재하기에 dLoss/dw1, dLoss/dw2..... dLoss/dw9999 까지 구해야 한다.
ChainRule
dLoss/dw1을 구하기 위해서는 수식에 미분 연산을 진행해야 한다. 이때 chainrule을 활용할 수 있다는 뜻인데, 보통 chainrule의 방법과 그 과정의 예시정도 숙지하고 역전파 과정을 다 이해했다는 경우가 많다.
미분에 대한 심층 이해
먼저 chainrule에 대한 증명이다. chainrule이 어떻게 가능한지, 즉 dL/dx = dL/dy x dy/dx 이 연산이 어떻게 가능한건지에 대한 관점이다. 분수식이면 당연하지만, 미분기호는 하나의 약속이다. 즉 우리의 궁금증은 미분식이 정말로 분수식의 연산을 따르냐에 대한 검증이 필요하다. 아래는 엄밀한 증명은 아니고 도구를 통한 간접적 증명이다.
증명을 위한 간단한 도구로 tan(theta)를 해당 지점의 기울기로 볼 수 있다는 특징을 활용하도록 한다. 그렇게 y와 t는 아래의 식으로도 활용될 수 있고 dt를 x에 관한 식으로 연결해주면 dy/dx = f'(t)xg'(x)라는 식이 도출된다. 우리가 증명하고자 하는 것은 dy/dx가 연쇄법칙을 따를 수 있느냐에 대한 관점이었으므로, f'(t) = dy/dy 와 g'(x) = dt/dx를 그대로 붙여준다면 dy/dx = dy/dt x dt/dx가 되므로 dt두개가 소거됨을 알 수 있다.
Chainrule 활용
dLoss / dw1를 구한다고 가정하고 w1은 합성함수 가장 깊숙한 곳에 위치한 변수라고 가정할 때 우리는 Chainrule을 통해 껍데기를 하나하나 벗겨가는 과정으로 dLoss/dw1을 찾아가는 연산을 진행한다.
곧바로 계산하지 않고, dLoss/활성화함수1 x d활성화함수1/d활성화함수2 x d활성화함수2/dw1 이런 방식으로 추적해 가는 것이다.
Q. 그냥 수식 전체를 풀어헤쳐서 편미분하면 안되나요?
일부 함수는 펼쳐놓고 편미분하기가 매우 어려울 수 있다. 특히, 복잡한 신경망 모델에서는 편미분을 통해 도출된 수식이 매우 복잡해지고, 이를 해석하는 것이 어렵게 된다. 이때 체인룰을 활용하면 전체 모델의 기울기를 간단하게 계산할 수 있으므로, 모델의 학습 과정을 효율적으로 구현할 수 있게 된다. 또한, 체인룰은 자동 미분(automatic differentiation) 알고리즘에서도 사용되므로, 신경망 등에서 많이 사용되는 역전파(Backpropagation) 알고리즘에서도 중요한 역할을 하게 된다.
구해진 미분값을 활용
chainrule을 활용해서 모든 가중치들에게 가중치들이 변할 때 Loss가 어떻게 변하는지에 대한 정보를 주었다. (dLoss/dwi : 특정 가중치에 대한 손실함수 기울기 값) 이 정보를 어떻게 활용하여 가중치 자신을 바꿔야 할까
가중치들은 역전파과정의 마무리로, 자신의 가중치 값을 바꾸게 된다. 이때 미분값에는 학습률이라는 수치가 함께 더해지고 가중치 값에서 빼게 된다 수식으로는,
w_update = w_original - learning_late(학습률) x dLoss/dw_original 이 된다.
미분값을 원래 가중치에 대해 빼는 이유
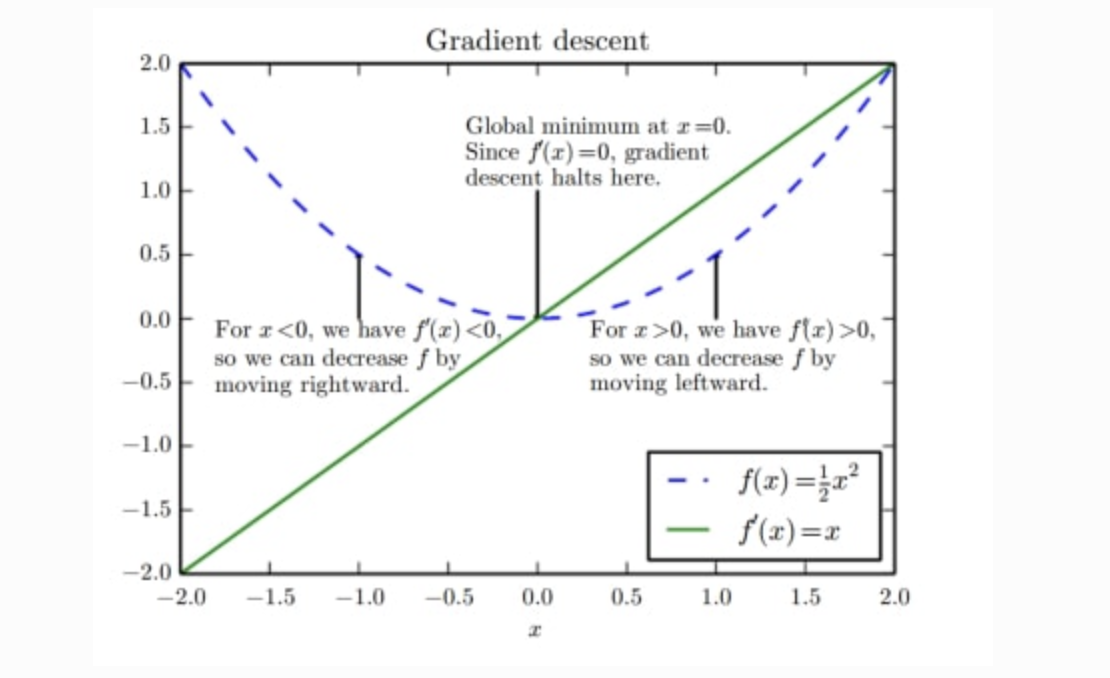
빼는 이유는 우리가 찾아야할 손실함수의 최솟값을 구하기 위해서이다. 우리가 도달해야할 목표는 최솟값이며 최솟값 지점에서의 미분값, 즉 기울기는 0이다. 만약 양의 기울기가 발생했다면 최솟값 지점으로부터 양의 방향에 가중치 값이 위치, 즉 오른쪽 지점에 현재 가중치값이 형성되있으므로 빼주게 되며 음의 기울기일 경우 최솟값 지점으로부터 음의 방향에 위치하므로 더해주어야 한다.
이렇게 모든 가중치에 대해 업데이트를 완료했다면 역전파 과정이 끝난 것이다.
학습 과정 정리
-
순전파(forward propagation)
입력층에서 시작하여, 각 층에서 활성화 함수를 통해 출력값을 계산하며, 이를 다음 층으로 전달
출력층에서는 손실 함수(loss function)를 통해 출력값과 실제값(target)의 차이인 오차를 계산 -
역전파(backward propagation)
출력층에서 시작하여, 손실 함수의 값을 이용해 출력층의 가중치(weight)를 조정
그 다음, 이전 층으로 오차를 전파시키며, 이전 층의 가중치를 조정합니다.
이 과정을 입력층까지 반복 -
가중치 업데이트
역전파 알고리즘이 모든 데이터에 대해 수행된 후, 각 가중치의 변화량을 계산하고 이를 이용해 가중치를 업데이트
일반적으로 경사하강법(gradient descent)과 같은 최적화 알고리즘을 사용하여, 손실을 최소화하는 가중치를 탐색
이러한 과정을 여러 번 반복하면서 가중치를 업데이트하고 손실을 최소화하는 것이 인공신경망의 기본적인 학습개념이다.
