컨볼루션을 활용한 일반화
7장에서 완전연결신경망의 성능에는 한계가 있었다. 검증셋에서 전혀 효과적이지 못했으며 이는 일반화의 실패라고 볼 수 있다. 완전연결신경망의 경우 너무 많은 파라미터가 필요하고(모든 뉴런끼리의 연결이기에) 사진데이터의 특성을 전혀 반영하지 못하며 모든 픽셀을 독립적으로 다루게 되었다. 이미 많은 파라미터가 필요한 상황에서 이 단점을 극복하기 위해 데이터 증강까지 필요한 상황이었다.
컨볼루션
이 챕터에서는 컨볼루션이 어떻게 인접한 픽셀들을 사용하고, 위치 변화에 대한 불변성 즉 픽셀들이 이동하더라도 이것을 쉽게 잡아낼 수 있는 컨볼루션을 공부해보도록 한다. 하늘을 나는 비행기와 같은 물체와 일치하는 패턴을 인지하려면 인근 픽셀의 배열 방식을 살펴봐야 한다. 즉 비행기가 등장하는 이미지에 나무나 구름 혹은 타 물체들이 구석에 존재하는 상황에 관심이 없어야 한다.
이 개념을 수학적으로 바꾸려면 픽셀 기준으로 이미지 내 멀리 떨어진 픽셀이아닌 주위의 픽셀에 대한 가중치의 합을 계산하면 된다.
컨볼루션의 역할
평행이동 불변성(translation invariance)는 지역화된 패턴이 이미지의 어떤 위치에 있더라도 동일하게 출력에 영향을 주는 성질이다. 컨볼루션은 2차원 이미지에 가중치 행렬을 스칼라곱을 수해하는 것으로 정의한다. 이 가중치 행렬은 커널(Kernel)이라 부르며 입력의 모든 이웃에 대해 수행한다.
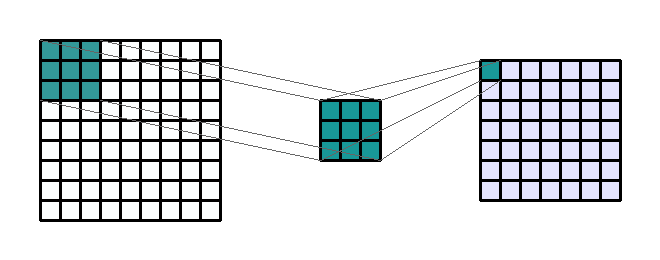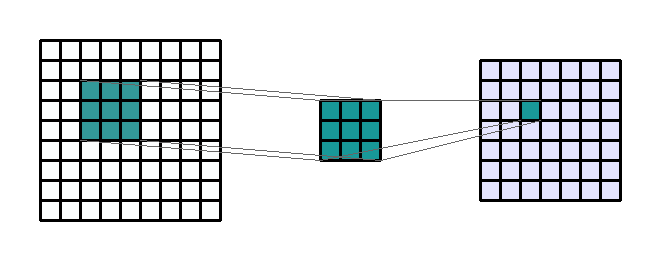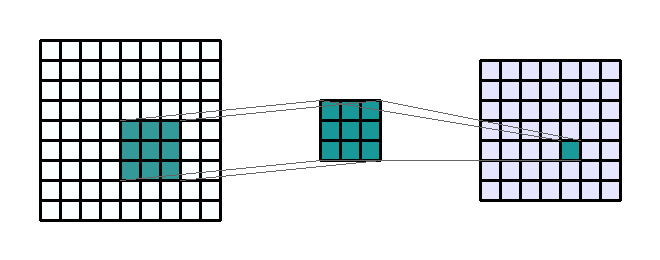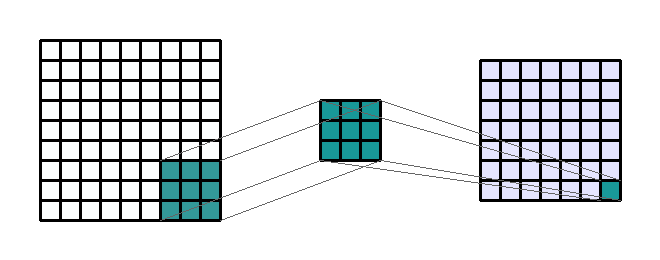RGB 이미지처럼 채널이 여러 개인 경우 가중치 행렬(커널)은 3개가 존재할 것이며 이를 합쳐서 출력값 계산에 기여하게 된다. 커널의 가중치는 처음에 랜덤으로 초기화되고 역전파를 통해 업데이트 된다.
이렇게 컨볼루션을 사용하면, 주위 영역에 대한 지역 연산을 할 수 있고, 평행이동 불변성을 가지게 되며, 더 적은 파라미터를 사용한다.(커널에 대한 가중치만으로 파라미터 수가 작아짐)
컨볼루션 사용해보기
torch.nn 모듈은 1,2,3차원에 대한 컨볼루션을 제공한다. nn.Conv1d는 시계열용이고 nn.Conv2d는 이미지용이며 nn.Conv3d는 용적 데이터나 동영상용이다. CIFAR-10데이터에 대해서는 2차원용인 nn.Conv2d를 사용한다. 전달해야할 인자는 입력 피처 수와 출력 피처 수, 커널의 크기가 있어야 한다.
커널의 크기는 일반적으로 모든 방향으로 동일하게, 홀수로 만든다( kernel_size = 3이라면 3x3으로)
conv = nn.Conv2d(3, 16, kernel_size=3)
# 커널사이즈로 (3,3)을 전달해도 됨.
# RGB채널의 피처 수는 3개, 이를 입력피처로 처음 인자로 전달하고 16개의 출력피처를 받기로
# 가중치 텐서는 출력텐서에 맞게 (16,3,3,3)가 될 것이다. 편향값의 크기는 16이 될 것이다.
이전의 완전연결 신경망에서의 가중치 개수와 비교해보면 가중치 수가 매우 줄어든 모습을 볼 수 있다. 2차원 Conv층 전달은 2차원 이미지를 출력한다.
출력피처를 16개로 늘린 이유
RGB 이미지 데이터이므로 픽셀당 피처는 3개이다. 이를 출력에서는 16개로 늘린다. 즉 가중치행렬인 필터를 16개를 만든 것이고 이것을 3번씩 총 48번의 컨볼루션 연산을 수행하게 된다. 이는 입력 특성 맵에서 더 다양한 특징을 추출하고 표현하기 위함이다. 더 다양한 특징을 추출하는 원리는 무엇일까? 이는 가중치 초기화때의 무작위성에 의거한다.
가중치가 만약 모두 같은 값으로 초기화 된다면 같은 데이터로 가중치가 학습됨으로써 필터의 값이 훈련 후에도 비슷한 표현을 가질 것이지만, 여러 가중치 필터가 모두 랜덤하게 초기화하기 때문에 훈련을 진행하면서 가중치 값들이 사진 데이터의 여러 표현을 학습하게 된다.
경계 패딩
입력이미지와 필터만 설정한다면, 필터가 입력이미지를 훑으면서 더 작아지는 출력이미지를 구성하게 된다. 이는 이미지의 경계에서 이뤄지는 작업에 부작용을 일으킨다. 즉 3x3의 필터의 경우 필터의 가장 중앙에 위치한 부분이 이미지의 모서리부분에 위치할 수 없기 때문에 학습에 있어서 이미지의 가장자리 부근의 정보가 손실될 수 있다. 이를 위해서 출력이미지와 입력이미지의 크기를 같게 하기 위해 입력이미지의 크기를 키우는, 이미지의 경계의 값이 0인 가짜픽셀을 패딩해주는 패딩기능이 파이토치에 존재한다.
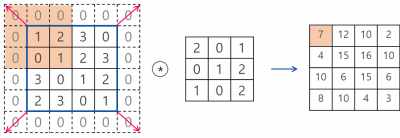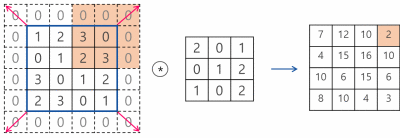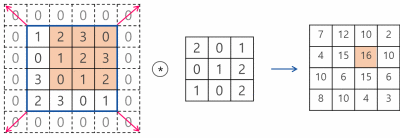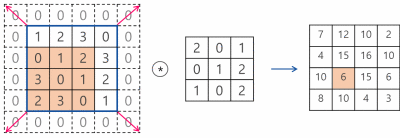
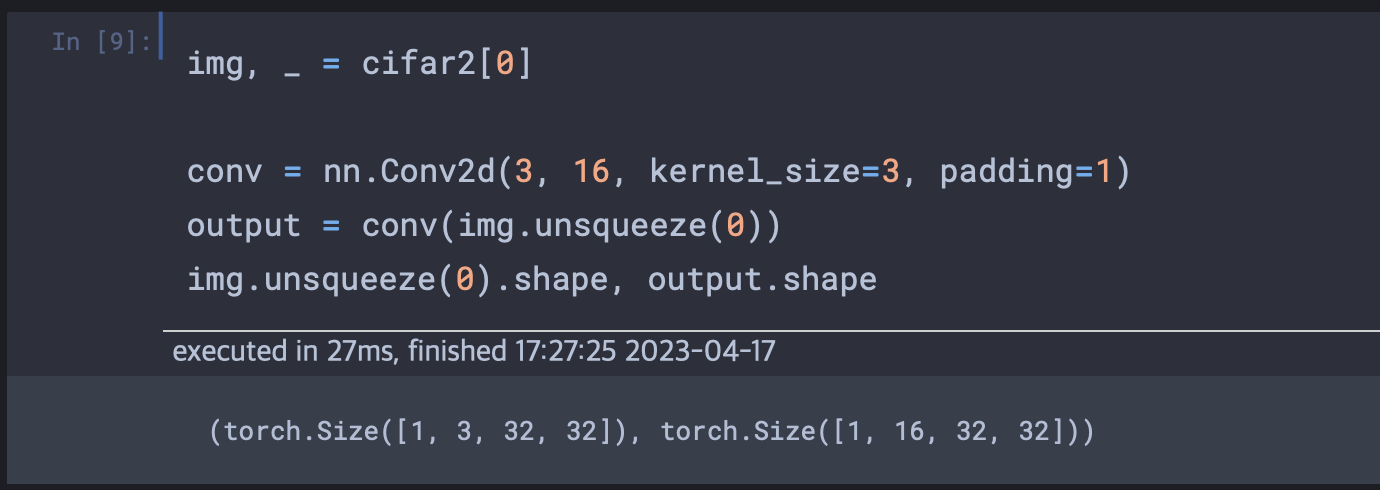
컨볼루션으로 피처 찾아내기
앞장에서 weight나 bias는 역전파를 통해 학습되는 파라미터라고 배웠다. 정확히는 nn.Linear에서 일어났다. 컨볼루션에서는 직접 가중치를 설정했다(필터구성) 실제 학습시 가중치는 랜덤으로 처음 구성되지만, 우선 커널을 직접 설정하면서 입력이미지와 출력이미지의 차이를 관찰해보도록 하자.
이를 위해 bias는 0으로 설정하여 배제하도록 한다.
with torch.no_grad():
conv.bias.zero_()
with torch.no_grad():
conv.weight.fill_(1.0 / 48.0)
fig = plt.figure(figsize=(15,7))
rows = 1
cols = 2
ax1 = fig.add_subplot(rows, cols, 1)
ax1.imshow(output[0,0].detach(), cmap='gray')
ax1.set_title('output')
ax1.axis("off")
ax2 = fig.add_subplot(rows, cols, 2)
ax2.imshow(img[0].detach(), cmap='gray')
ax2.set_title('input')
ax2.axis("off")
예상가능하게, 입력에 비해 출력의 이미지가 흐려졌다. 각 출력 픽셀은 자신의 주변 픽셀에 대한 평균이기 때문이다. 다음으로는 커널을 다음과 같이 바꾸어본다.
conv = nn.Conv2d(3, 16, kernel_size=3, padding=1)
with torch.no_grad():
conv.weight[:] = torch.tensor([[-1.0, 0.0, 1.0],
[-1.0, 0.0, 1.0],
[-1.0, 0.0, 1.0]])
conv.bias.zero_()
output = conv(img.unsqueeze(0))
fig = plt.figure(figsize=(15,7))
rows = 1
cols = 2
ax1 = fig.add_subplot(rows, cols, 1)
ax1.imshow(output[0,0].detach(), cmap='gray')
ax1.set_title('output')
ax1.axis("off")
ax2 = fig.add_subplot(rows, cols, 2)
ax2.imshow(img[0].detach(), cmap='gray')
ax2.set_title('input')
ax2.axis("off")가중치 텐서를 저렇게 바꾼 이유가 무엇일까? 필터의 모든 값은 더해져서 평균이 된다 즉 이 커널은 가운데 픽셀기준 오른쪽 픽셀에서 왼쪽 픽셀을 빼게 될 것이다. 만약 오른쪽 픽셀과 왼쪽 픽셀이 비슷한 값을 가진다면 출력 이미지에 형성되는 값은 0에 가까울 것이다. 가장자리의 경우 패딩에 의해 0값이 존재한다. 안쪽 값과의 차이를 생각한다면 가장자리에서 강조되는 높은 출력값을 가지게 된다.
실제로 오른쪽 왼쪽 가장자리 부근이 높은 출력값으로 탐지되고 있음을 출력 이미지를 통해 확인가능하다. 전통적으로 필터 설계는 컴퓨터 비전 전문가의 역할로 이러한 필터를 최적으로 조합하여 이미지의 특징을 강조하는 식으로 물체를 인식해왔으나, 딥러닝을 통해 이제는 커널을 자동으로 만들게 된다.
- 딥러닝에서 가중치 행렬인 필터는 초기에 자동으로 값이 구성된다. 훈련을 통해 여러 표현을 학습하게 되고 사진 데이터의 특징을 잡을 수 있는 필터가 완성된다. ( 초기 랜덤 가중치로 형성된 필터가 많이 형성되어야 하는 이유를 알 수 있다.)
깊이와 풀링
완전연결 계층에서 컨브넷으로 넘어오면서 지역성이나 평행이동 불변성을 해결했다. 또한 작은 커널을 사용하기를 추천했다. 작은 커널을 추천한 이유는 이 정도의 크기가 지역성의 한계이기 때문이다. 하지만 이미지안의 물체나 구조가 3~5픽셀 이상의 크기를 가지는 경우도 많을 것이다. 이때 작은 커널은 해당 지역을 모두 커버하지 못한다. 그렇다면 어떻게 이 문제를 해결해야할까?
- 더 큰 커널을 사용할 수 있지만, 이는 완전 연결 계층의 아핀 변환으로 수렴해서 컨볼루션의 장점을 잃어버리게 된다.
큰 이미지에서 작은 이미지로
다운샘플링에는 여러 방법이 존재한다. 이미지를 반으로 줄이는 것은 이웃하는 네 개의 픽셀을 입력 받아어떠한 과정을 거친 후 한 픽셀을 출력하는 작업이다.어떠한 과정은 우리가 정의할 수 있다.
- 네 개의 픽셀 평균(average pooling)
- 네 개의 픽셀중 최댓값(max pooling) - 오늘날 가장 널리 사용됨
- 스트라이드하며 컨볼루션 수행, N번째 픽셀만 계산
맥스 풀링
가장 널리 사용되지만, 데이터의 4분의 3을 버린다는 단점이 있다. 2x2 인접 픽셀에서 최댓값을 뽑는다는 것은 약한 신호는 버리고 살아남은 피처를 발견하는 과정이다. 파이토치에는 nn.MaxPool2d 모듈이 존재하고 입력인자로는 풀링 연산을 수행할 인접한 영역 크기를 받는다.
이제 컨볼루션과 다운샘플링의 조합이 어떻게 큰 패턴을 식별하는지 알아보자. 패딩을 통해 입력 이미지와 컨볼루션 출력의 크기는 동일하다. 커널을 통과해 재구성된 출력은 맥스 풀 층을 거쳐 반으로 줄어든다. 이 과정을 여러번 반복하면 출력 이미지 데이터의 shape는 매우 작아질 것이다.
- 초반의 과정에서 커널은 비교적으로 이미지의 세부를 탐색하여 표현을 반영하며, 출력의 shape가 더 작아질수록 더 넓은 범위의 지역에 대해 표현을 반영한다. 풀링작업이 없다면, 각 과정은 모두 같은 규모의 지역만 탐색하고 학습하여 표현을 반영하게 될 것이다.
우리의 신경망에 적용하기
model = nn.Sequential(
nn.Conv2d(3, 16, kernel_size=3, padding=1),
#(3, 32, 32) -> (16, 32, 32)
nn.Tanh(),
nn.MaxPool2d(2),
# (16, 32, 32) -> (16, 16, 16)
nn.Conv2d(16, 8, kernel_size=3, padding=1),
#(16, 16, 16) -> (8, 16, 16)
nn.Tanh(),
nn.MaxPool2d(2),
#(8, 16, 16) -> (8, 8, 8)
nn.Linear(8 * 8 * 8, 32)),
nn.Tanh()
nn.Linear(32, 2)nn.Linear의 입력을 8 x 8 x 8로 받은 이유는 위 주석에서 변화된 최종 출력 이미지의 shape때문이므로 과정을 잘 이해해야한다.
하지만 위 코드는 에러가 발생한다. 마지막 주석에도 나타나있지만, 마지막 맥스풀링층을 거친 출력데이터는 shape가 (8,8,8)이다 이것을 바로 입력으로 512로 넣을 수 없기 때문이다. shape에 대한 변화가 필요하다.
nn.Module 서브클래싱하기
Sub-module
서브 모듈(submodule)은 nn.Module을 상속받아 만들어진 객체를 말한다. 예를 들어, 위의 예시에서는 Conv2d, Tanh, MaxPool2d, Linear 등이 nn.Module을 상속받아 만들어진 서브 모듈이다. 이 서브 모듈들은 Net 클래스의 메소드 안에서 사용된다. 단, 직접 만든 클래스가 nn.Module을 상속받아 만들어진 경우에도 해당 클래스는 서브 모듈로 취급된다.
# 서브클래싱
class Net(nn.Module):
def __init__(self):
super().__init__() # 상속
self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
self.act1 = nn.Tanh()
self.pool1 = nn.MaxPool2d(2)
self.conv2 = nn.Conv2d(16, 8, kernel_size=3, padding=1)
self.act2 = nn.Tanh()
self.pool2 = nn.MaxPool2d(2)
self.fc1 = nn.Linear(8 * 8 * 8, 32)
self.act3 = nn.Tanh()
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = self.pool1(self.act1(self.conv1(x)))
out = self.pool2(self.act2(self.conv2(out)))
out = out.view(-1, 8 * 8 * 8) # <1>
out = self.act3(self.fc1(out))
out = self.fc2(out)
return out나만의 클래스로 구성한 이유
위의 코드 변환은 주로 코드의 가독성과 재사용성을 높일 수 있다. nn.Sequential을 사용하여 레이어를 연속적으로 쌓는 방법은 간단하지만, 각 레이어를 하나씩 정의하고 초기화하는 방법이 더욱 유연하고 가독성이 좋다. 따라서 위의 코드 변환은 nn.Module을 상속받아서 필요한 레이어들을 각각 변수로 정의하고, forward 함수에서 각 레이어를 차례대로 호출하는 방식으로 변경되었으며, 이렇게 변경된 코드는 레이어를 추가하거나 제거하기 쉽고 또 다른 모델에서도 재사용하기 용이하다.
- 추가적으로 .view를 통해 shape의 수정의 단계를 추가하였다.
파이토치가 파라미터와 서브모듈을 유지하는 방법
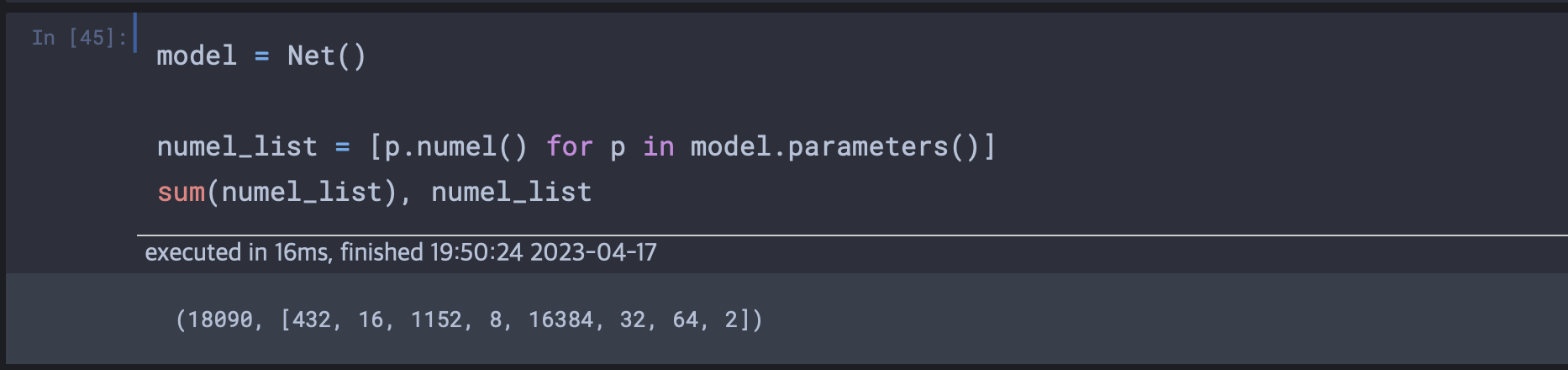
앞서 코드에서는 생성자 안에 nn.Module의 속성에 nn.Module의 인스턴스를 할당했다. 즉 서브모듈들을 속성에 구성하였다. 이렇게 하면 Net은 사용자의 추가 행위 없이 서브모듈의 파라미터에 접근가능하다
이제 모듈을 직접 만드는 법을 알았으며 이렇게 직접 클래스를 만드는 기법은 2부에서 많이 필요할 것이니 미리 습관화 해놓도록 하자.
클래스 초기화와 forward()
PyTorch에서는 init() 메서드에서 모듈이 사용할 레이어를 정의하고, forward() 메서드에서 실제 데이터를 받아와 레이어들을 연결하여 계산하는 작업을 수행한다.
따라서 init()에서 모듈이 사용할 레이어들을 정의하고 초기화하는 작업을 수행하고, forward()에서는 정의된 레이어들을 연결하여 데이터를 처리한다.
코드에서도 init()에서는 레이어들을 정의하고 초기화하고, forward()에서는 정의된 레이어들을 연결하여 데이터를 처리한다. 이렇게 모듈의 초기화와 데이터 처리를 분리함으로써 코드를 더욱 모듈화하고 가독성을 높일 수 있다.
함수형 API
생성자에서 서브모듈을 등록하는 과정을 고려하면 파라미터가 없는 nn.Tanh나 nn.MaxPooling2d 같은 서브 모듈은 굳이 등록할 필요가 없을 것 같다. 당연히 그렇다! 그러한 이유로 파이토치는 모든 nn 모듈에 대한 함수형을 제공한다.
Question. nn.tanh()를 그냥 호출하면 안되나?
nn.Tanh()는 학습 가능한 매개변수를 가지지 않는다. nn.Tanh()는 단순히 Tanh 함수를 적용하는 것뿐만 아니라, 학습 가능한 매개변수를 가진 다른 nn.Module과 함께 사용될 때, 그 모듈의 출력에 Tanh 함수를 적용하는 것이다. nn.Tanh()은 nn.Module을 상속하고 있기 때문에, nn.Sequential 등에서 nn.Module들과 함께 사용될 수 있다. 이렇게 모듈들을 합쳐서 구성한 네트워크를 학습할 때, nn.Tanh()은 학습 가능한 매개변수를 가진 다른 모듈들과 함께 최적화된다. 따라서 nn.Tanh()은 Tanh 함수를 적용하는 것뿐만 아니라, 학습 가능한 매개변수를 가진 다른 모듈과 함께 사용될 때 유용하다.
nn.Module API는 Parameter라는 모습으로 상태를 저장하고 순방향 전달에 필요한 명령 집합을 서브모듈로 저장하는 컨테이너로 이해할 수 있다.
책에서는 forward()메서드에 F.tanh()를 최종적으로 구성했지만, 전반적으로 모델의 학습 성능에 큰 영향을 주는 것은 아니다. 하지만 모델의 구성과 가독성을 개선하는 데 도움이 될 수 있다. 따라서 nn.Tanh()를 생성자에서 사용하는 것과 forward() 메서드에서 F.tanh()를 사용하는 것은 모두 올바른 방법이다. 하지만 일관성 있는 코드를 작성하는 것이 가독성과 유지 보수에 도움이 될 수 있기 때문에, 보통은 하나의 방식으로 코드를 작성해야한다.
우리가 만든 컨볼루션 신경망 훈련시키기
먼저 우리가 만든 컨볼루션 신경망은 중첩된 두 루프를 가지고 있음을 주목하자. 바깥 루프는 에포크 단위로, 안쪽 루프는 DataLoader 단위로 돈다.
- 모델에 입력값 주입(순방향 전달)
- 손실값 계산(순방향 전달2)
- 이전 기울기값 0으로 리셋(zero_grad())
- loss.backward() 호출하여 모든 파라미터에 대한 손실값 기울기 계산(역전파)
- 옵티마이저를 통해 손실값 낮추도록 파라미터 조정(학습)
# 훈련 과정 정의
import datetime # <1> 시간도 보이기 위함
def training_loop(n_epochs, optimizer, model, loss_fn, train_loader):
for epoch in range(1, n_epochs + 1):
# <2> 에포크 for루프로
loss_train = 0.0
for imgs, labels in train_loader:
# <3> 배치 for루프로
outputs = model(imgs)
# <4> model에 입력값 주입
loss = loss_fn(outputs, labels)
# <5> 손실값 계산(예측값, 타겟값)
optimizer.zero_grad()
# <6> 이전 기울기 값 0으로 리셋
loss.backward() # <7>
# loss에 대한 미분값 추적
optimizer.step() # <8>
# 옵티마이저로 파라미터 수정
loss_train += loss.item()
# <9> 에포크동안 손실값 모두 더하기(.item()을 통해 손실값을 파이썬 수로 변환)
if epoch == 1 or epoch % 10 == 0: # 에포크동안 중간결과 보이기
print('{} Epoch {}, Training loss {}'.format(
datetime.datetime.now(), epoch,
loss_train / len(train_loader))) # <10>train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=True)
# <1> train_loader 만들기
model = Net()
# <2> model 서브 클래스 객체 생성
optimizer = optim.SGD(model.parameters(), lr=1e-2)
# <3> 옵티마이저 정의
loss_fn = nn.CrossEntropyLoss()
# <4> 손실함수 정의
training_loop( # <5> 정의된 훈련루프에 하이퍼파라미터 및 데이터 주입
n_epochs = 100,
optimizer = optimizer,
model = model,
loss_fn = loss_fn,
train_loader = train_loader,
)
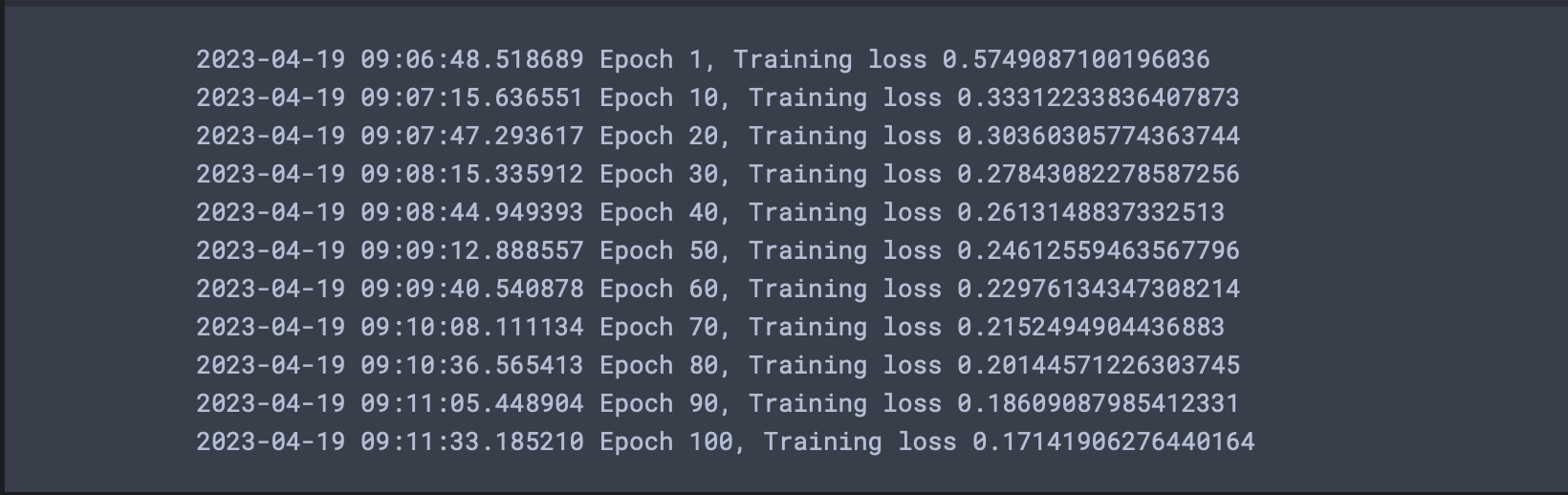
정확도 측정
손실값이 낮아지는 것을 확인했다. 더 직관적으로 이해가 쉬운 정확도를 측정해보도록 한다.
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=False)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size=64,
shuffle=False)
def validate(model, train_loader, val_loader):
for name, loader in [("train", train_loader), ("val", val_loader)]:
correct = 0
total = 0
with torch.no_grad(): # <1> 기울기 계산 끄기(지표 측정만 할 것이니까.)
for imgs, labels in loader:
outputs = model(imgs)
_, predicted = torch.max(outputs, dim=1) # <2> 가장 높은 확률의 것 선택
total += labels.shape[0] # <3> 전체
correct += int((predicted == labels).sum()) # <4> 타겟 = 예측인 것만
print("Accuracy {}: {:.2f}".format(name , correct / total))
validate(model, train_loader, val_loader)
# 실행결과
# Accuracy train: 0.93
# Accuracy val: 0.89GPU에서 훈련시키기
device = (torch.device('cuda') if torch.cuda.is_available()
else torch.device('cpu'))
print(f"Training on device {device}.")- 위 코드 실행시 gpu에 옮길 수 있다면 device는 cuda를 출력하며, 그렇지 않다면 cpu를 출력한다.
Apple Silicon의 경우
실제로 위 코드를 실행시키면 필자의 M1에서는 "cpu"를 출력했다. M1 Mac은 Apple의 자체 칩셋인 Apple Silicon을 사용하기 때문에 기존의 NVIDIA나 AMD의 GPU와는 다른 구조를 가지고 있다. 그렇기 때문에 기존의 CUDA와 호환되지 않으며, 현재는 Rosetta를 통해 x86 버전의 CUDA와 호환성을 제공하고 있다. 하지만 이로 인해 성능 저하가 발생할 수 있기 때문에, M1 Mac에서는 Apple이 제공하는 Metal이나 Apple's Accelerate 프레임워크 등의 기술을 사용하여 GPU 가속을 이용할 수 있다. PyTorch에서는 이러한 Apple의 기술을 지원하고 있기 때문에 M1 Mac에서도 GPU 가속을 이용할 수 있다. 다만, 일부 모델이나 작업에 따라서는 성능이 다소 떨어질 수 있을 수 있다.
import torch
print(torch.cuda.is_available())
print(torch.version.cuda)
print(torch.backends.metal.is_available())
# 다음과 같은 코드로 cuda와 metal의 지원여부를 확인가능하다.mac의 경우 cuda방식이 불가능하기 때문에, metal(apple silicon으로 gpu가속 효과)을 지원하는 pytorch를 재설치해야하는데, anaconda가상환경과 macos-version, pytorch를 모두 재구성해야 하며 아직 해당 버전이 정식출시된 것이 아니기에 적용하진 않았다.
# gpu가속으로 훈련하는 코드 .to()로 device인자로 전달하면 된다
train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64,
shuffle=False)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size=64,
shuffle=False)
all_acc_dict = collections.OrderedDict()
def validate(model, train_loader, val_loader):
accdict = {}
for name, loader in [("train", train_loader), ("val", val_loader)]:
correct = 0
total = 0
with torch.no_grad():
for imgs, labels in loader:
imgs = imgs.to(device=device)
labels = labels.to(device=device)
outputs = model(imgs)
_, predicted = torch.max(outputs, dim=1) # <1>
total += labels.shape[0]
correct += int((predicted == labels).sum())
print("Accuracy {}: {:.2f}".format(name , correct / total))
accdict[name] = correct / total
return accdict
all_acc_dict["baseline"] = validate(model, train_loader, val_loader)모델 설계
현재 우리의 모델의 목적은 새와 비행기의 분류이다. 즉 비교적 복잡하지 않은 경우이다. 만일 이미지넷처럼 더 크고 복잡한 이미지에서 답을 찾으려면, 여러 시각적 단서를 찾기 위해 계층적 구조화가 필요하다.
메모리 용량 늘리기: 너비
신경망의 너비 차원을 주목해보자. 이는 신경망 계층 내의 뉴런 수 혹은 컨볼루션의 채널 수에 해당하는 값이다. 이를 기반으로 현재의 모델을 넓혀보도록 한다. 출력 채널 수를 더 크게하고, 이어지는 계층도 이에 맞추는 것이다.
즉 모델의 뉴런을 더 많이 구성하여 모델을 키우는 작업으로 이는 모델의 용량과 비용을 증가시킨다.(파라미터수의 증가)
모델의 일반화 돕기: 정규화
모델 훈련은 중요한 두 단계를 거친다. 하나는 최적화 단계로, 훈련셋에 대해 손실값을 줄이는 단계이고, 다른 하나는 일반화 단계로 모델이 훈련셋뿐 아니라 이전에 겪어보지 않은 검증셋에 대해서도 적절하게 동작하는지를 검사하는 것이다. 이 두 단계를 정규화(regularization)라고 한다.
가중치 페널티
손실값에 정규화 항을 넣는 방법으로 정규화 항을 조작해서 모델의 가중치가 상대적으로 작게 만드는 것이다. 즉 훈련을 통해 증가할 수 있는 크기를 제한하는 것으로 큰 가중치 값에 페널티를 부과하는 것이다. 가장 유명한 정규화 항으로 L2 정규화와 L1정규화가 있다.
- L2 정규화 : 모델의 모든 가중치에 대한 제곱합
- L1 정규화 : 모델의 모든 가중치의 절댓값 합
가중치 감쇠 : L2 정규화
L2 정규화는 가중치 감쇠라고도 하며, L2정규화 값이 모든 가중치에 더해지는 것이다. L2 정규화는 가중치 벡터의 L2 노름을 손실 함수에 더해줌으로써 가중치가 작아지도록 규제하며 L2 정규화의 미분값은 가중치 벡터의 미분값과 같이 손실 함수의 미분값에 곱해져서 역전파된다. 따라서 L2 정규화는 가중치의 크기를 감소시키는 효과가 있다.
드랍아웃
드랍아웃 개념은 처음 제프리 힌튼 그룹에서의 논문에서 제시되었으며, 개념은 매우 간단하다. 훈련을 반복할 때마다 신경망의 뉴런 출력을 랜덤하게 0으로 만드는 작업을 일어나게 하는 것이다. 이 때문에, 신경망이 각 입력 샘플을 암기하려는 기회를 줄이므로 과적합을 방지한다.
파이토치에서는 모듈 사이에 nn.Dropout모듈을 넣어 모델의 드랍아웃을 구현할 수 있다.
배치 정규화
배치 정규화(Batch Normalization)는 딥 뉴럴 네트워크에서 학습을 안정화시키기 위한 방법 중 하나이다. 각 층(layer)의 입력값을 해당 배치의 평균과 분산으로 정규화(normalization)한 다음에, 정규화된 값을 선형 변환과 활성화 함수 적용 전에 scaling과 shifting한다. 이를 통해 학습을 더욱 안정화시키고, 학습 속도를 빠르게 하고, 정확도를 높일 수 있다.
배치 정규화에서 scaling과 shifting은 평균과 분산을 조정하는 작업을 말한다. 일반적으로 평균은 0으로, 분산은 1로 조정하여 데이터의 분포를 표준 정규분포로 만드는 것이다.
하지만 이 작업을 수행할 때마다 정확히 평균이 0이 되고 분산이 1이 되는 것은 아니기 때문에 scaling과 shifting 파라미터를 추가하여 이를 조절한다. Scaling 파라미터는 표준편차, 즉 분산의 제곱근을 조절하는 역할을 하며, shifting 파라미터는 평균값을 조절하는 역할을 한다. 따라서 이 파라미터를 통해 최종적으로 평균과 분산을 조정할 수 있다.
배치 정규화는 미니배치 단위로 입력값을 정규화(normalize)하는 것이 특징이다. 즉, 훈련 데이터의 한 묶음(batch)에서 데이터 분포의 특징을 추정해서 이를 바탕으로 정규화한다. 미니배치마다 정규화를 하는 것은 배치마다 입력값의 분포가 다르기 때문에 각 배치마다 분포를 맞추는 것이 도움이 되는 것이다.
배치 정규화의 이점
1. 초기 가중치 설정에 덜 민감하게 되어 초기화 과정이 간소화 됨.
2. Gradient Vanishing 문제를 완화시키며, Gradient Exploding 문제를 방지
3. 높은 Learning rate를 사용하여도 안정적으로 학습
4. Regularization 효과가 있어 Overfitting을 방지
5. 데이터의 평균과 분산을 정규화하는 과정이 과적합을 방지하기 위한 Dropout과 유사한 역할을 함
더 복잡한 구조 : 깊이
뉴런의 수를 증가 시키는 것이 너비의 증가라고 두번째로는 깊이가 있다. 모델이 얕은 경우보다 깊은 경우가 항상 좋은걸까? 이것은 상황마다 다르다. 컴퓨터 비전 관점에서 얕은 신경망은 사진에서 사람의 모습을 식별가능하지만 신경망이 깊어질수록 상반신의 얼굴과 얼굴내 세부요소까지 구별해낼 수 있다.
스킵 커넥션
2015년까지만 해도 딥러닝 모델의 계층은 20개 이상 늘어나기 어려웠다. 역전파를 생각해볼 때, 파라미터에 대한 손실함수의 미분은 더 이전 계층의 경우 미분 연산의 체인 연결에서 오는 많은 수로 곱해져야 한다. 곱하는 수의 일부분이 특정하게 작다던가 크다면 최종 미분값에 영향을 크게 끼치게 된다. 즉, 체인이 길게 이어지는 경우 기울기 값에 기여하는 파라미터가 사라지는 vanishing gradient문제가 발생한다. 이 문제때문에 파라미터 값들은 적절하게 업데이트되지 못한다.
잔차 신경망(residual network -ex. ResNet)은 단순한 트릭으로 매우 깊은 신경망이어도 성공적으로 훈련되는 잔차 신경망인 레즈넷을 만들어 신경망이 수십 개의 계층에서 100개의 계층으로 늘어나게 되었다. 스킵 커넥션은 입력을 계층 블럭의 출력에 연결하는 것이다. 즉 잔차연결을 하지 않은 출력이 f(x)라면, 잔차연결을 한 출력은 f(x) + x 가 된다.
잔차연결이 기울기 소실을 해결하는 논리
레이어1과 레이어2가 있다고 가정하고 레이어2에 잔차연결이 되어있다면 최종출력으로 레이어2의 출력값과 레이어2의 입력값이 더해진 값이 된다. 레이어2의 파라미터가 수정될 때 기존에는 레이어2 출력값의 미분값만을 활용했다면 잔차연결 레이어의 경우 레이어2 출력값의 미분값 뿐만아니라 레이어2의 입력(레이어1의 출력)의 미분값 또한 파라미터 수정에 기여한다. 즉 wlayer2 = w_layer2 - lr x (d레이어2출력, d레이어1출력)이 될 것이다. 자동적으로 레이어1의 파라미터가 갱신될 때도 레이어1출력에 대한 직접적인 미분값을 부여받아 기울기 소실에 대한 문제가 이전보다 해결될 수 있다.
class NetRes(nn.Module):
def __init__(self, n_chans1=32):
super().__init__()
self.n_chans1 = n_chans1
self.conv1 = nn.Conv2d(3, n_chans1, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(n_chans1, n_chans1 // 2, kernel_size=3,
padding=1)
self.conv3 = nn.Conv2d(n_chans1 // 2, n_chans1 // 2,
kernel_size=3, padding=1)
self.fc1 = nn.Linear(4 * 4 * n_chans1 // 2, 32)
self.fc2 = nn.Linear(32, 2)
def forward(self, x):
out = F.max_pool2d(torch.relu(self.conv1(x)), 2)
out = F.max_pool2d(torch.relu(self.conv2(out)), 2)
out1 = out # 잔차연결 구현을 위해 결괏값을 out1변수에 빼놓기(다음 레이어에서의 입력값)
out = F.max_pool2d(torch.relu(self.conv3(out)) + out1, 2)
# 이전 레이어의 출력값, 즉 현재 레이어의 입력값과 현재 레이어의 출력값을 합쳐서
# 다음 풀링레이어로 전달
out = out.view(-1, 4 * 4 * self.n_chans1 // 2)
out = torch.relu(self.fc1(out))
out = self.fc2(out)
return out