
시계열(timeseries)데이터는 일정한 간격으로 측정하여 얻은 모든 데이터를 말하며, 지금까지 보았던 데이터와 달리 시스템의 역학을 이해해야한다.
분류: 하나 이상의 범주형 레이블을 시계열에 부여한다이벤트 감지: 연속된 데이터 스트림에서 예상되는 특정 이벤트 발생을 식별한다.이상치 탐지: 연속된 데이터 스트림에서 발생하는 비정상적인 현상을 감지한다. 일반적으로 비지도 학습으로 수행된다.
온도 예측 문제
이번 장에서 모든 코드 예제는 건물 지붕 위의 센서에서 최근 기록된 기압, 습도와 같은 매 시간 측정값의 시계열이 주어졌을 때 24시간 뒤의 온도를 예측하는 것이다. 타겟 값인 기온을 그래프로 나타낸 것은 다음과 같다.
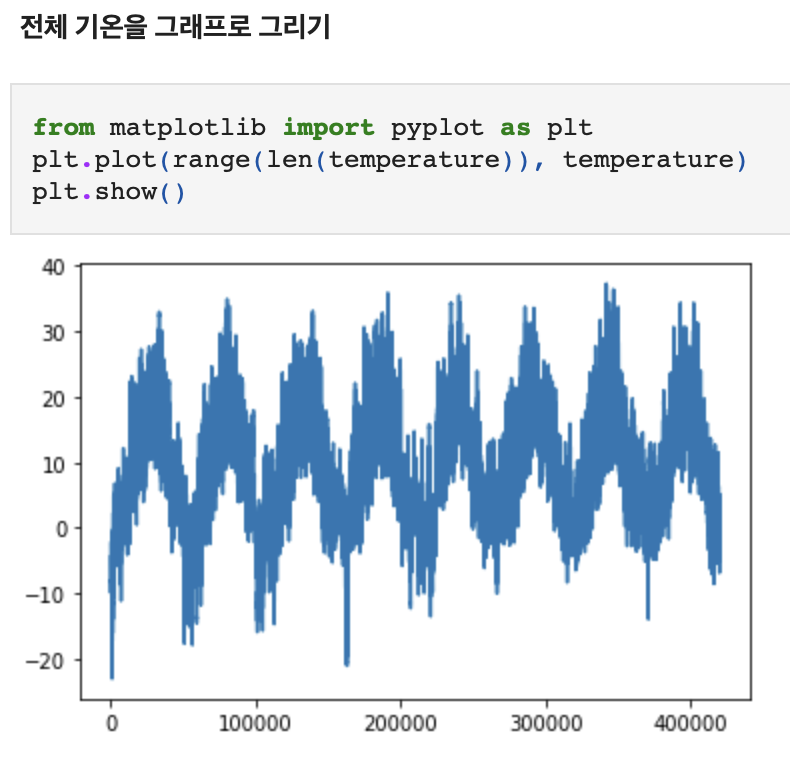
split
데이터는 총 42만 551개이며 주기성을 보인다. 데이터 전체를 넘파이 배열로 만들고 온도를 하나의 배열로, 나머지 데이터를 또 다른 배열로 만든다. 두번째의 경우가 미래 온도를 예측하기 위한 feature이다. 이때 'Datetime'열은 제외시킨다.
처음 50%의 데이터를 훈련에 사용하며, 25%를 검증, 25% 테스트로 사용한다.
- 이때 검증 데이터와 테스트 데이터가 훈련 데이터보다 최신이어야 한다.
데이터 준비
이 문제의 정확한 정의는 한 시간에 한 번씩 샘플링 된 5일간의 데이터가 주어졌을 때 24시간 뒤의 온도를 예측할 수 있는지이다.
데이터는 이미 수치형이기에 어떤 벡터화도 필요하지 않으며, 특성들의 스케일이 각기 다르기 때문에 각 시계열을 독립적으로 정규화하여 비슷한 범위를 가진 작은 값으로 바꾸도록 한다.
그리고, 과거 5일치 데이터와 24시간 뒤 타깃 온도의 배치를 반환하는 Dataset 객체를 만든다. timeseries_dataset_from_array()를 사용하여 훈련, 검증, 테스트를 위해 3개의 데이터셋을 만든다.
# 정규화
mean = raw_data[:num_train_samples].mean(axis=0)
raw_data -= mean
std = raw_data[:num_train_samples].std(axis=0)
raw_data /= std
sampling_rate = 6 # 시간당 하나의 데이터 포인트가 샘플링 된다.
sequence_length = 120 # 이전 5일간(120시간) 데이터를 사용
# 시퀀스의 타깃은 시퀀스 끝에서 24시간 후의 온도이다.
delay = sampling_rate * (sequence_length + 24 - 1)
batch_size = 256
train_dataset = keras.utils.timeseries_dataset_from_array(
raw_data[:-delay],
targets=temperature[delay:],
sampling_rate=sampling_rate,
sequence_length=sequence_length,
shuffle=True,
batch_size=batch_size,
start_index=0,
end_index=num_train_samples)
val_dataset = keras.utils.timeseries_dataset_from_array(
raw_data[:-delay],
targets=temperature[delay:],
sampling_rate=sampling_rate,
sequence_length=sequence_length,
shuffle=True,
batch_size=batch_size,
start_index=num_train_samples,
end_index=num_train_samples + num_val_samples)
test_dataset = keras.utils.timeseries_dataset_from_array(
raw_data[:-delay],
targets=temperature[delay:],
sampling_rate=sampling_rate,
sequence_length=sequence_length,
shuffle=True,
batch_size=batch_size,
start_index=num_train_samples + num_val_samples)기준점
시계열 데이터는 연속성이 있고 일자별로 주기성을 가진다고 가정할 수 있다. 오늘온도는 내일 온도와 비슷할 확률이 높다. 그렇기에 상식 수준의 해결책은 지금으로부터 24시간 후 온도는 동일하다고 예측하는 것이다. 이 방법을 MAE로 평가해 보도록 한다.
기본적인 모델 제작
from tensorflow import keras
from tensorflow.keras import layers
# shape지정
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
x = layers.Flatten()(inputs)
x = layers.Dense(16, activation="relu")(x)
outputs = layers.Dense(1)(x) # without activation
model = keras.Model(inputs, outputs)
callbacks = [
keras.callbacks.ModelCheckpoint("jena_dense.keras",
save_best_only=True)
]
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_dataset,
epochs=10,
validation_data=val_dataset,
callbacks=callbacks)
model = keras.models.load_model("jena_dense.keras")
print(f"테스트 MAE: {model.evaluate(test_dataset)[1]:.2f}")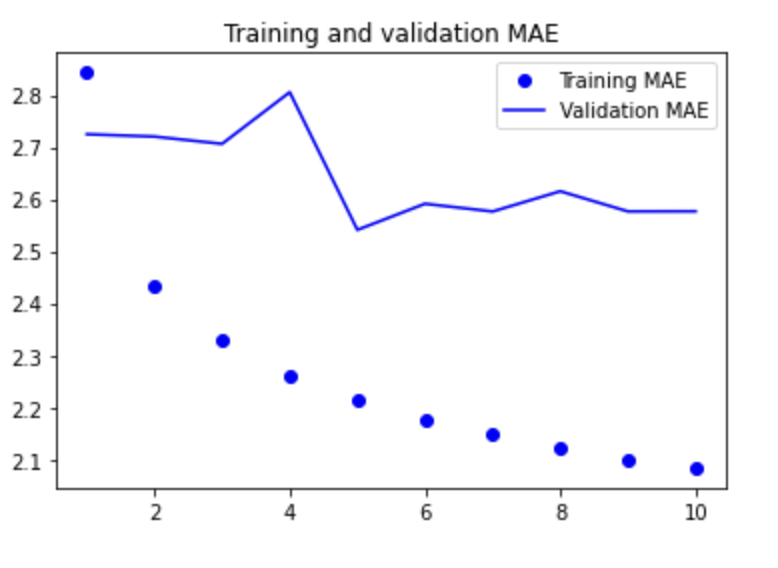
일부 검증 손실은 학습을 사용하지 않은 기준점에 가까우나 안정적이지 못하다. 기준 모델의 성능을 앞지르기가 쉽지 않다. 문제 해결을 위해 탐색하는 모델의 가설공간은 우리가 매개변수로 설정한 2개의 층을 가진 네트워크의 모든 가능한 가중치 조합이다. 상식 수준의 모델은 이 공간에서 표현가능한 수백만 가지 중 하나일 뿐이며, 좋은 솔루션을 경사하강법으로 찾을 수 없다는 것이다.
1D ConvNet 적용
Conv1D층은 1D 윈도우를 사용하여 입력 시퀀스를 슬라이딩한다. 초기 윈도우 길이를 24로 정하고 Maxpooling으로 시퀀스를 다운샘플링하여 윈도우 크기를 줄여나간다.
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
x = layers.Conv1D(8, 24, activation="relu")(inputs)
x = layers.MaxPooling1D(2)(x)
x = layers.Conv1D(8, 12, activation="relu")(x)
x = layers.MaxPooling1D(2)(x)
x = layers.Conv1D(8, 6, activation="relu")(x)
x = layers.GlobalAveragePooling1D()(x)
outputs = layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
callbacks = [
keras.callbacks.ModelCheckpoint("jena_conv.keras",
save_best_only=True)
]
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_dataset,
epochs=10,
validation_data=val_dataset,
callbacks=callbacks)
model = keras.models.load_model("jena_conv.keras")
print(f"테스트 MAE: {model.evaluate(test_dataset)[1]:.2f}")1D ConvNet의 경우 밀집 연결모델보다 성능이 떨어진다.
- 날씨 데이터는 평행 이동 불변성 가정을 많이 따르지 않는다. 데이터에 일별 주기성이 존재하지만, 아침 데이터와 저녁 데이터는 성질이 다르다. 날씨 데이터는 매우 특정한 시간 범위에 대해서만 평행 이동 불변성을 가진다.
- 이 데이터는 순서가 매우 중요하다. 최근 데이터가 5일 전 데이터보다 내일 온도를 예측하는 데 훨씬 유용하다. 즉 1D ConvNet은 이러한 영향을 가중시켜 고려할 수 없다. 특히 최대풀링과 전역평균풀링 층에서 순서정보가 많이 삭제된다.
밀집 연결모델이나 합성곱 모델이 잘 작동하지 않는 이유는 밀집연결모델의 경우 시계열 데이터를 펼쳤기 때문에 입력 데이터에서 시간 개념을 잃어버렸으며, 합성곱 모델은 데이터의 모든 부분을 비슷한 방식으로, 풀링을 적용하여 데이터가 압축되며 순서정보를 잃어버렸다.
LSTM 모델
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
x = layers.LSTM(16)(inputs)
outputs = layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
callbacks = [
keras.callbacks.ModelCheckpoint("jena_lstm.keras",
save_best_only=True)
]
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_dataset,
epochs=10,
validation_data=val_dataset,
callbacks=callbacks)
model = keras.models.load_model("jena_lstm.keras")
print(f"테스트 MAE: {model.evaluate(test_dataset)[1]:.2f}")드디어 상식 수준의 모델을 앞질렀다!
밀집 연결 네트워크나 컨브넷처럼 지금까지 본 모든 신경망의 특징은메모리가 없다는 것이다. 즉 전체 시퀀스를 하나의 데이터 포인토로 변환해야한다. 이와 반대로 사람은 문장을 읽을 때 이전에 나온 것을 기억하면서 단어별로 또는 한눈에 들어오는 만큼씩 처리한다. 내부모델을 유지하며 점진적으로 정보를 처리하는 것이다.
- RNN은 시퀀스의 원소를 순회하며 지금까지 처리한 정보를
상태에 저장한다.- 여전히 하나의 시퀀스를 하나의 데이터포인트 즉 하나의 입력으로 간주되지만 이것은 한 번에 처리되지 않는다.
RNN 정방향 계산 넘파이로 구현
import numpy as np
timesteps = 100
input_features = 32
output_features = 64
inputs = np.random.random((timesteps, input_features))
state_t = np.zeros((output_features,))
W = np.random.random((output_features, input_features))
U = np.random.random((output_features, output_features))
b = np.random.random((output_features,))
successive_outputs = []
for input_t in inputs:
output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)
successive_outputs.append(output_t)
state_t = output_t
final_output_sequence = np.stack(successive_outputs, axis=0)결국 RNN은 반복할 때 이전에 계산한 정보를 재사용하는 for루프에 지나지 않는다. 출력은 계속해서 successive_outputs 리스트에 쌓이며 state_t는 다음 노드로가서 다음 시간의 입력과 함께 활성화함수로 계산되어 output이 된다. 이 출력은 다시 그 상태에 기록되어 다음 노드로 전달되는 동시에 출력리스트에 쌓이게 된다. 최종적 출력은 (timesteps, output_features) 크기의 랭크-2 텐서가 된다.
- keras의 SimpleRNN은 위와 같지만 하나의 시퀀스가 아닌 시퀀스의 배치를 처리한다는 점에서 한가지 차이가 존재한다. 그렇기에 입력으로 (batch_size, timesteps, input_features)크기의 입력을 받는다.
케라스에 있는 모든 순환 층은 두 가지 모드로 실행가능하다. 각 타임스텝의 출력을 모은 전체 시퀀스 크기의 랭크-3 텐서를 반환하거나 입력 시퀀스의 마지막 출력 크기의 랭크-2 텐서만 반환할 수 있다. 생성자의 return_sequences 매개변수로 제어가능하다.
- 네트워크의 표현력을 증가시키기 위해 여러 개의 순환 층을 차례로 쌓는 것이 유용할 때가 있다. 이때에는 중간층들이 전체 출력 시퀀스를 반환하도록 설정해야한다.
LSTM , GRU detail
LSTM은 RNN의 그레이디언트 소실 문제에 대한 연구의 결정체이다. RNN의 변종으로, 잔차연결과 굉장히 비슷한 아이디어를 가진다.
RNN의 구조에 타임스텝을 가로질러 정보를 나르는 데이터 흐름을 추가해보자. 이 데이터흐름을 이동 상태라고 한다. 이동 상태는 입력 연결과 상태에 연결된다. 그런 후 타임스텝으로 전달될 상태에 영향을 미친다(활성화 함수와 곱셈연산을 통해).
RNN에서 출력 y = activation(dot(state_t, U) + dot(input_t, W) + b) 는 세개의 변환을 가진다. 3개의 변환 모두 자신만의 가중치 행렬을 가진다.
LSTM 구조의 의사코드를 주목하자. 이 또한 RNN처럼 3개의 다른 변환이 관련되어있다.
output_t = activation(c_t) *
activation(dot(input_t, W0) +
dot(state_t, U0) + b0)
i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi)
f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bi)
k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bi)
c_t+1 = i_t * k_t + c_t + f_t즉 새로운 이동상태 계산에는 입력데이터의 정보와 이전 이동상태에 대한 정보 그리고 출력의 정보 세가지가 계산되어 c_t+1를 구성하여 다음 output_t를 계산할 때 사용된다.
c_t와 f_t의 곱셈은 이동을 위한 데이터 흐름에서 관련이 적은 정보를 의도적으로 삭제하는 것이다. i_t *k_t는 현재에 대한 정보를 제공하고 이동 트랙을 새로운 정보로 업데이트한다.
이 과정은 훈련 반복마다 매번 새로 시작되며 셀의 구조가 셀이 하는 일을 결정하지 않기에 셀의 구조를 완벽하게 이해할 필요가 없으며, LSTM 셀의 역할만 기억하면 된다. 그것은 바로 과거 정보를 나중에 다시 주입하여 그레이디언트 소실 문제를 해결하는 것이다.
순환 신경망의 고급 사용법
- 순환 드롭아웃 : 드롭아웃의 한 종류로 순환 층에서 과대적합을 방지
- 스태킹 순환 층 : 모델의 표현능력을 증가시키나 비용이 증가한다
- 양방향 순환 층 : 순환 네트워크에 같은 정보를 다른 방향으로 주입하여 정확도를 높이고 기억을 좀 더 오래 유지시킨다.
드롭아웃
훈련 데이터를 층에 주입할 때 데이터에 있는 우연한 상관관계를 깨뜨리기 위해 입력 층의 유닛을 랜덤하게 끄는 기법이다. 타임스텝마다 랜덤하게 드롭아웃 마스크를 바꾸는 것이 아니라 동일한 드롭아웃 마스크를 모든 타임스텝에 적용해야한다. 케라스에서 dropout은 2개의 매개변수를 가진다. 또한 드롭아웃을 적용한 모델의 경우 수렴하는 데 언제나 훨씬 더 오래 걸리게 된다.
- 입력에 대한 드롭아웃 비율 조절
- 순환 상태의 드롭아웃 비율 조절
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
# 훈련 속도를 놓이기 위해 순환 드롭아웃을 제외합니다.
#x = layers.LSTM(32, recurrent_dropout=0.25)(inputs)
x = layers.LSTM(32)(inputs)
x = layers.Dropout(0.5)(x)
outputs = layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
callbacks = [
keras.callbacks.ModelCheckpoint("jena_lstm_dropout.keras",
save_best_only=True)
]
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_dataset,
epochs=50,
validation_data=val_dataset,
callbacks=callbacks)스태킹 순환 층
드롭아웃 등을 사용하여 과대적합을 줄이는 기본단계를 거쳤다면 과대적합이 일어날 때까지 모델의 용량을 늘리는 것이 좋다. 일반적으로 층의 유닛의 개수를 늘리거나 층을 더 많이 추가한다. 역시나 순환 층을 차례로 쌓기 위해서는 모든 중간층은 마지막 타임스텝 출력만 아니고 전체 시퀀스를 출력해야한다(return_sequence = True). GRU는 LSTM의 간소화된 버전으로 매우 비슷하다. 이를 사용해서 드롭아웃과 2개의 순환 층을 스태킹한다.
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
# 훈련 속도를 놓이기 위해 순환 드롭아웃을 제외합니다.
# x = layers.GRU(32, recurrent_dropout=0.5, return_sequences=True)(inputs)
# x = layers.GRU(32, recurrent_dropout=0.5)(x)
x = layers.GRU(32, return_sequences=True)(inputs) # 전체 시퀀스로 출력
x = layers.GRU(32)(x) #마지막 층
x = layers.Dropout(0.5)(x) # 드롭아웃
outputs = layers.Dense(1)(x) #출력 층
model = keras.Model(inputs, outputs)
callbacks = [
keras.callbacks.ModelCheckpoint("jena_stacked_gru_dropout.keras",
save_best_only=True)
]
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_dataset,
epochs=50,
validation_data=val_dataset,
callbacks=callbacks)
model = keras.models.load_model("jena_stacked_gru_dropout.keras")
print(f"테스트 MAE: {model.evaluate(test_dataset)[1]:.2f}")양방향 RNN 사용하기
자연어 처리에서는 즐겨 사용되는 것이 양방향 RNN으로 특정 작업에서 기본 RNN보다 훨씬 좋은 성능을 보인다. 양방향 RNN은 RNN이 순서에 민감하다는 점을 이용한다.
케라스에서는 Bidirectional 층을 사용하여 양방향 RNN을 만든다. 이 클래스는 첫 번째 매개변수로 순환 층의 객체를 전달 받는다. 클래스는 전달받은 순환 층을 새로운 두 번째 객체를 만든다. 하나는 시간 순서대로 입력 시퀀스를 처리하며, 다른 하나는 반대 순서로 처리한다.
inputs = keras.Input(shape=(sequence_length, raw_data.shape[-1]))
# 훈련 속도를 놓이기 위해 순환 드롭아웃을 제외합니다.
# x = layers.LSTM(32, recurrent_dropout=0.25)(inputs)
x = layers.LSTM(32)(inputs)
x = layers.Dropout(0.5)(x)
outputs = layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
model.compile(optimizer="rmsprop", loss="mse", metrics=["mae"])
history = model.fit(train_gen,
epochs=10,
steps_per_epoch=819,
validation_data=val_gen,
validation_steps=410)온도 예측 문제에서는 일반 LSTM보다 성능이 떨어지는 모습이다. 이는 당연하다. 역방향으로 시퀀스를 처리하는 것이 날씨데이터에 대해서는 의미가 없기 때문이다. 동시에 네트워크 용량은 2배가 되고 훨씬 더 일찍 잘못된 학습과 함께 과대적합된다.
