Chaper2. 신경망의 수학적 구성 요소
딥러닝을 이해하기 위해서는 텐서, 텐서 연산, 미분, 경사하강법등의 개념에 친숙해져야한다. 2장에서는 이러한 이해를 위해 MNIST 데이터를 활용한다.
텐서(Tensor)
모든 머신 러닝 시스템은 일반적으로 텐서를 기본 데이터 구조로 사용한다. 텐서는 데이터를 위한 컨테이너(container)이다. 일반적으로 수치형 데이터를 다루므로 숫자를 위한 컨테이너이다.
스칼라(랭크 - 0 텐서)
하나의 숫자만을 담고 있는 텐서를 스칼라 또는 스칼라 텐서 , 0D텐서라고 부른다. 스칼라 텐서의 축의 개수는 0이다. 축의 개수를랭크(rank)라고도 부른다.
벡터(랭크 - 1 텐서)
숫자의 배열을벡터(vector)또는 랭크-1텐서, 1D텐서라고 부른다. 벡터는 딱 하나의 축을 가진다. [1,2,3,4,5]는 5개의 원소를 가진 5차원 벡터라고 부른다.
- 5D 벡터와 5D 텐서를 혼동하지 말 것!!
차원 수 (dimenstionality) : 특정 축을 따라 놓인 원소의 개수
행렬(랭크 - 2 텐서)
벡터의 배열은행렬(matrix)또는 랭크-2텐서, 2D텐서라고 부른다. 행렬에는 2개의 축이 있으며 보통 행(row), 열(column)이라고 부른다.
이러한 행렬들을 하나의 새로운 배열로 합치면 랭크-3텐서가 된다. 이러한 랭크-3텐서들을 하나의 배열로 합치면 랭크-4 텐서가 만들어진다.
- 딥러닝에서는 보통 랭크0에서 4까지의 텐서를 다룬다.
텐서의 핵심 속성
- 축의 개수(랭크)
- 크기(shape)
- 데이터 타입(dtype)
MNIST 살펴보기
MNIST의 훈련데이터는 다음과 같은 텐서 속성을 가진다.
축의 개수 : train_images.ndim : 3
배열의 크기 : train_images.shape : (60000, 28, 28)
데이터 타입 : train_images.dtype : uint8
이 배열은 8비트 정수형 랭크-3 텐서이다. 정확하게는 28 x 28 크기의 정수 행렬 6만개가 있는 배열이다. 각 행렬은 하나의 흑백 이미지이며, 행렬의 각 원소는 0~255 사이의 값을 가진다.
배치 데이터
일반적으로 딥러닝에서 사용하는 모든 데이터의 텐서의 첫 번째 축은샘플 축(sample axis)이다. mnist에서는 숫자 이미지가 샘플이 된다.
딥러닝 모델은 한 번에 전체 데이터셋을 처리하지 않고 작은 `배치(batch)로 나눈다.batch = train_images[:128] batch = train_images[128:256]...
텐서 연산
심층 신경망이 학슨한 모든 변환을 수치 데이터 텐서에 적용하는 몇 종류의 텐서 연산으로 나타낼 수 있다.
keras.layer.Dense(512, activation='relu') output = relu(dot(W, input) + b)keras의 Dense층은 행렬을 입력으로 받고 입력 텐서의. 새로운 표현인 또 다른 행렬을 반환하는 함수처럼 해석할 수 있다. 그것이 두번째 코드이다.
- 입력 텐서와 텐서W 사이의 점곱
- 점곱으로 만들어진 행렬과 벡터 b사이의 덧셈
- relu연산. relu(x) = max(x, 0)
실제로 배열의 연산을 직접 구현할 수 있지만 우리는 Numpy라이브러리를 기본으로 활용하여 연산을 구현한다. 실제로 직접 구현할 경우보다 Numpy는 원소별 연산을 엄청난 속도로 처리한다.
브로드캐스팅(broadcasting)
위에서 보다시피 "점곱으로 만들어진 행렬과 벡터b사이의 덧셈"은 크기가 다른 두 텐서가 더해지는 경우이다. 모호하지 않고 실행가능하다면 작은 텐서가 큰 텐서의 크기에 맞추어브로드캐스팅된다. 연산 규칙은 다음과 같다.
- 큰 텐서의 ndim에 맞도록 작은 텐서에 축이 추가된다.
- 작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복된다.
X의 크기는 (32, 10)이고 y의 크기는 (10,)이라고 가정해보자. 우리는 넘파이 메소드를 통해 y의 크기를 (1, 10)으로 바꿀 수 있다. 아래의 결과를 보면 배열의 껍데기가 하나 더 생긴 것을 볼 수 있다.
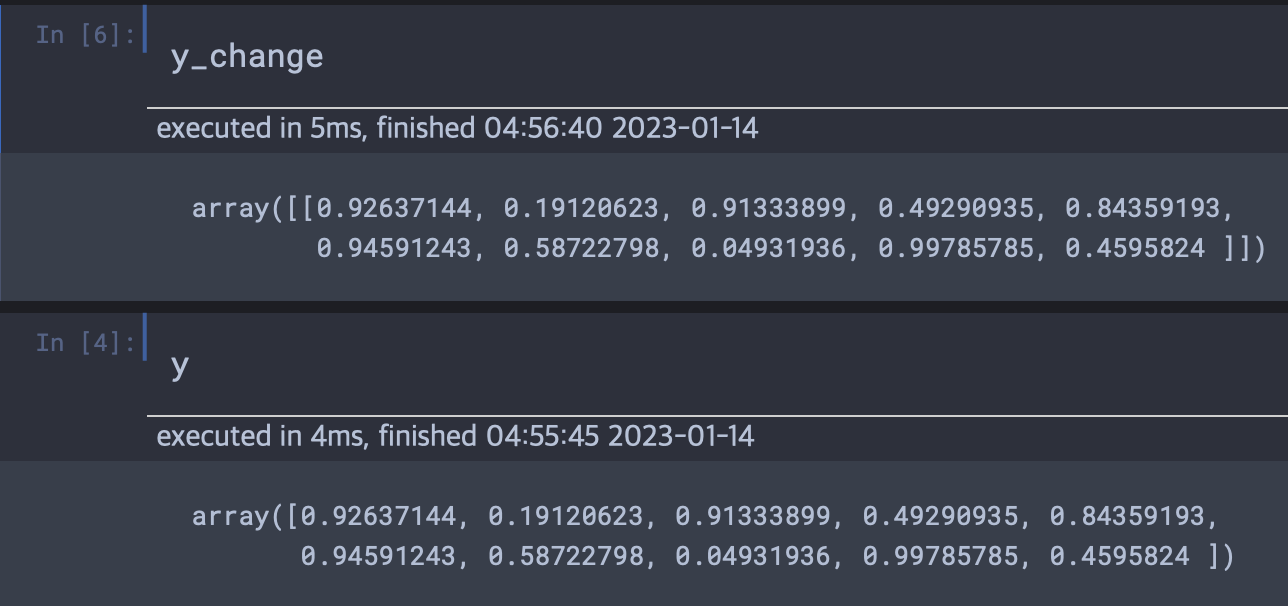
이렇게 (1,10)으로 만들어진 새로운 텐서의 샘플을 32개 복사하여 (32, 10)의 크기의 텐서로 바꾸어 (32, 10) + (32, 10)으로 크기를 맞춘다.
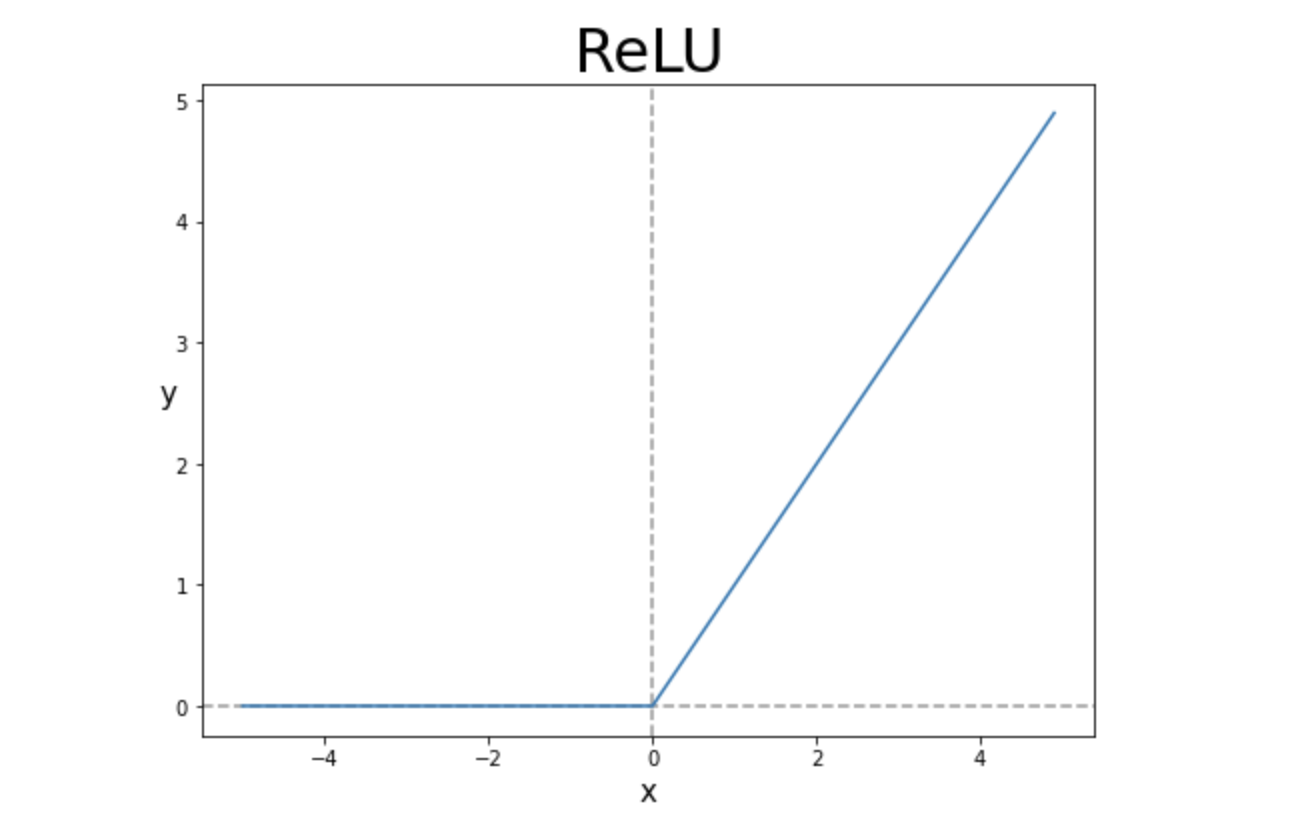
ReLU 분석
우리는 다음과 같은 ReLU함수를 활성화 함수로 자주 이용하게 된다. 위에서 텐서 연산의 예시로도 ReLU함수를 사용하였다. 그렇다면 h=max(0,a) where a=Wx+b 즉 ReLU는 왜 은닉층에서 자주 사용될까?
그것을 알기 위해서는 ReLU가 자주 쓰이기 이전에 sigmoid를 알고 가야한다.
기울기 소실 문제(Vanishing Gradient problem)는 역전파(Backpropagation) 알고리즘에서 처음 입력층(input layer)으로 진행할수록 기울기가 점차적으로 작아지다가 나중에는 거의 기울기의 변화가 없어지는 문제를 말한다.
이 문제의 원인은 활성화 함수(Activation function)로 시그모이드 함수(sigmoid function)을 사용하는데 이 함수의 특성으로 인해 기울기 소실 문제가 발생한다. 다음 sigmoid 함수와 sigmoid 함수의 미분 그래프를 보자.
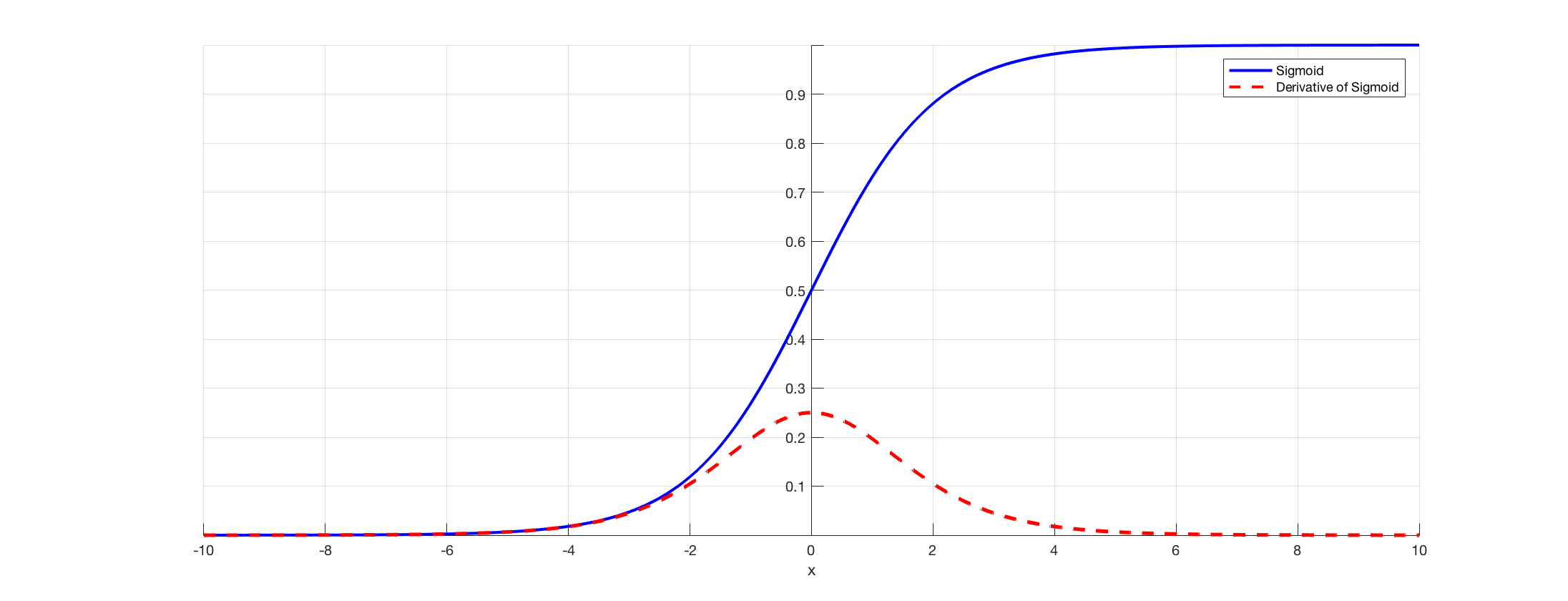
시그모이드(sigmoid)함수의 미분값을 보면 최대 0.25, 최소 0을 보이고 있다. 우리는 역전파의 과정에서 활성화 함수의 미분값을 입력층에 가까운 앞쪽의 layer로 갈수록 활성화 함수의 미분을 연쇄적으로 곱하게 된다. sigmoid의 미분의 최대가 0.25이기 때문에 만약 layer가 많아진다면 계산과정에서 0~0.25의 범위안에서의 값이 연속적으로 곱해지게 된다. 즉 앞쪽의 layer로 갈수록 기울기 값은 거의 0에 가깝게 작아져서 가중치의 수정이 거의 이루어지지 않게 된다.
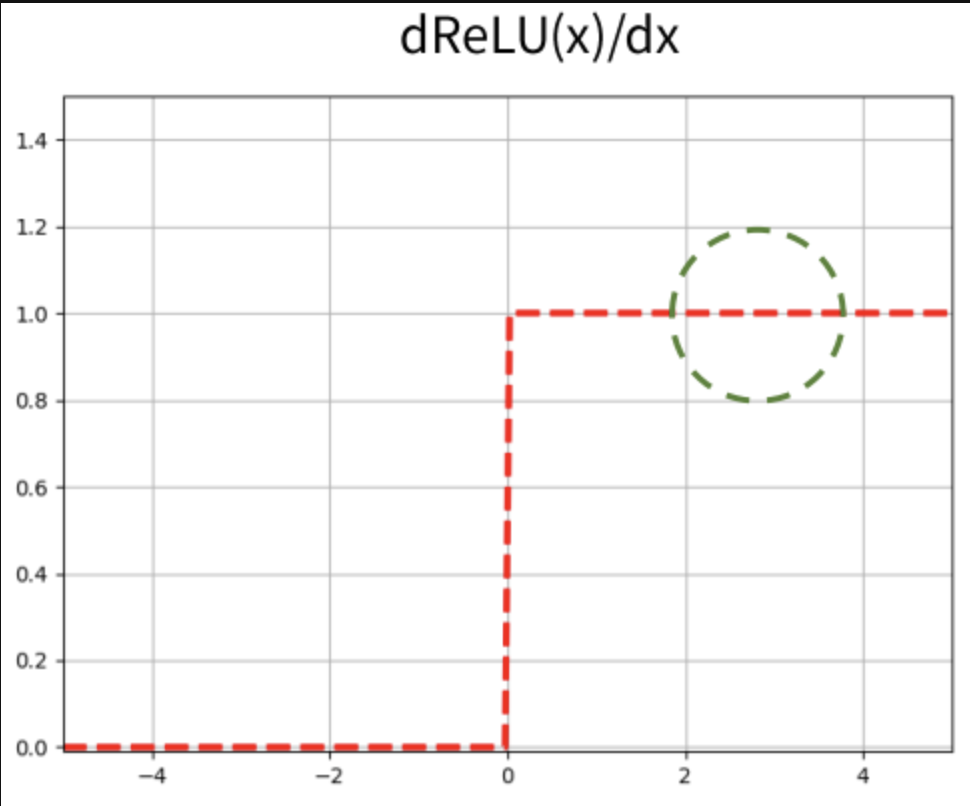
반면 ReLU의 미분을 보게 되면 0보다 클 때 기울기 값이 1인 것을 볼 수 있다. 즉 기울기 소실문제가 발생하지 않게 된다. 가중치 수정이 매우 작게 일어난다는 것은, 학습을 느리게하는 원인이 되는데 ReLU는 이러한 단점을 막아준다. 하지만 입력값이 음수일 경우 기울기가 0이 되어 가중치 업데이트가 안될 수 있고 이러한 현상을 Dying ReLU or Dead Neuron이라고 한다.
신경망의 엔진: 그레이디언트 기반 최적화
훈련
1. 훈련 샘플 x와 이에 상응하는 타깃 y_true의 배치를 추출한다.
2. x를 사용하여 모델을 실행(정방향 패스)하여 예측 y_pred를 구한다.
3. y_pred와 y_true의 차이를 측정하여 모델의 손실을 계산한다.
4. 배치에 대한 손실이 조금 감소되도록 모델의 모든 가중치를 업데이트한다.
확률적 경사 하강법
미분 가능한 함수가 주어지면 이론적으로 이 함수의 최솟값을 구할 수 있다. 함수의 최솟값은 도함수가 0인 지점이다. 따라서 우리가 할 일은 도함수가 0이 되는 지점을 모두 찾고 이 중에서 어떤 포인트의 함수 값이 가장 작은지 확인하는 것이다.
이를 신경망에 적용하면 가장 작은 손실 함수의 값을 만드는 가중치의 조합을 찾는 것을 의미한다.
또한 업데이트할 다음 가중치를 계산할 때 현재 그레이디언트 값만 보지 않고 이전에 업데이트된 가중치를 여러가지 다른 방식으로 고려하는 SGD변종들이 많이 존재한다.
- SGD, Adagrad, RMSprop...(모멘텀을 사용한 옵티마이저)
정방향 패스와 역방향 패스
입력 데이터가 처음 층에 들어와서 가중치를 곱하고 활성화함수에 넣어져 출력으로 나오는 값을 다음 층에 전달되고 이를 반복하여 최종 y_pred가 만들어진다. y_pred는 y_true와 비교되어 손실함수로부터 손실값을 받게 된다. 이러한 손실값은 거꾸로 이전의 입력데이터에 대해 미분한 값이 계산되고 미분의 연쇄법칙을 통해 가중치 수정을 위한 최종 미분값들이 생성된다.
텐서플로의 그레이디언트 테이프는 with문과 함께 사용하여 해당 코드 블록 안의 모든 텐서연산을 계산 그래프 형태로 기록한다.