케라스 창시자에게 배우는 딥러닝 CH4

Chaper4. 신경망 시작하기 : 분류와 회귀

4장에서는 keras.datasets에서 제공하는 데이터들을 통해 실제로 keras의 신경망을 활용하여 end-to-end 머신러닝 워크 플로우를 경험해본다.
총 3가지의 데이터가 주어지며 이진 분류 문제, 다중 분류 문제, 회귀 문제를 다루게 될 것이다.

이진 분류 문제

IMDB datasets를 활용한 이진 분류 (binary classification)모델을 만드는 것을 목적으로 한다.

IMDB Datasets info

Metadata	infomation
data_name	IMDB
train_data	samples : 25000
test_data	samples : 25000
labels	50% : 긍정 , 50% : 부정 (이진분류)
explain	데이터는 이미 각 단어 시퀀스가 숫자 시퀀스로 변환되어 있음.

from tensorflow.keras.datasets import imdb

(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)

keras 라이브러리에서 다음과 같이 다운로드 받을 수 있다. train_data는 여러 숫자로 이루어진 배열이며, 해당 숫자들은 어떠한 단어가 인코딩 된 것이다. train_labels는 0과 1로 이루어져 있다. (책에서는 재미삼아 인코딩된 배열을 디코딩하는 과정이 있는데 따로 게시글에 추가하지는 않았다)

신경망에 바로 train_data, 즉 숫자 배열을 주입할 수 없다. train_data의 각 sample들을 확인해보면, 모두 길이가 다르다. 그 이유는 해당 숫자들은 모두 단어이고, 리뷰마다 단어들이 얼마나 들어가 있는지는 모두 다르기 때문이다. 우리는 위 코드에서 num_words 파라미터를 통해 가장 많이 쓰인 단어 만개만을 제한하였다.

숫자를 가진 리스트를 멀티-핫 인코딩(multi-hot encoding)하여 0과 1의 벡터로 변환한다.
ex) [8,5] --> [0,0,0,0,0,1,0,0,1,0......0] 이렇게 바꾼다는 뜻

멀티-핫 인코딩(multi-hot encoding)
데이터를 양적 변수가 아닌 질적 변수로 다루기 위함이다. 또한 이렇게 인코딩 하게 되면, 케라스의 모델의 층에서 입력으로 데이터가 들어갈 때 모두 동일한 shape로 들어가게 될 것이다. 이와 비슷한 인코딩으로는 원-핫 인코딩(one-hot encoding)이 있으며 이는 0이 아닌 수(1)가 딱 한번 들어갈 때이다. 반면 멀티-핫 인코딩은 여러번 들어가게 된다.

데이터의 멀티-핫 인코딩을 위해 새로운 함수를 만든다.

import numpy as np

def vectorize_sequences(sequences, dimension=10000): 
    results = np.zeros((len(sequences), dimension)) # 행 : len(sequences) , 행 하나엔 0이 만개로 된 배열
    for i, sequences in enumerate(sequences): # 인덱스와 배열값을 동시에 받음 , 배열 값은 리스트 [n1, n2, .... nn]
        for j in sequences:
            results[i, j] = 1.
    return results

# 멀티 핫 인코딩
x_train = vectorize_sequences(train_data) # [1, 14, 47.....](길이:253) ->[0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0....](길이:10000)
x_test = vectorize_sequences(test_data)

# 멀티 핫 인코딩한 데이터로 하여금 신경망에 주입하게 됨.

---

신경망 모델 만들기
입력 데이터는 현재 벡터이며, 레이블은 스칼라(1 or 0)이다. 이러한 문제에서 가장 잘 작동하는 모델은 relu활성화 함수를 사용한 밀집 연결 층을 그냥 쌓는 것이다.
Dense 층을 쌓을 때 두가지 중요한 고민이 필요하다.

• 얼마나 많은 층을 사용할 것인가?
• 각 층에 얼마나 많은 유닛을 둘 것인가?
  (이러한 고민은 5장에서 해결)

해당 예제에서는 Dense층을 3개로 쌓았으며, 첫층과 두번째층의 units=16이며 활성화함수는 relu를 사용하였고, 마지막 층은 이진분류이므로 units=1이고 sigmoid를 활성화함수로 사용하였다.
마지막으로 손실 함수와 옵티마이저를 선택해야한다.

• 손실 함수 : binary_crossentropy( 유일한 선택은 아니지만, 확률을 출력하는 모델에서 손실함수는 크로스엔트로피가 최선의 선택이다.
• 옵티마이저 : rmsprop (일반적으로 거의 모든 문제의 기본 선택으로 좋다.)
• 검증 셋 설정 : 10000개를 따로 떼어서 x_val, y_var의 검증 셋과partial_x_train, partial_y_train의 훈련 셋을 만든다.(코드 미첨부)

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(1, activation='sigmoid')
])

model.compile(optimizer='rmsprop',
             loss='binary_crossentropy',
             metrics=['accuracy'])

history = model.fit(partial_x_train,
                   partial_y_train,
                   epochs=20,
                   batch_size=512,
                   validation_data=(x_val, y_val))

model.fit() 메소드는 history 객체를 반환한다. 이 객체는 훈련동안 발생한 모든 정보를 담고 있는 딕셔너리인 history 속성을 가진다.
history속성, 즉 이 딕셔너리에는 loss, accuracy, val_loss, val_accuracy가 담겨있다.

이 history를 이용하여, 시각화를 해보도록 한다.

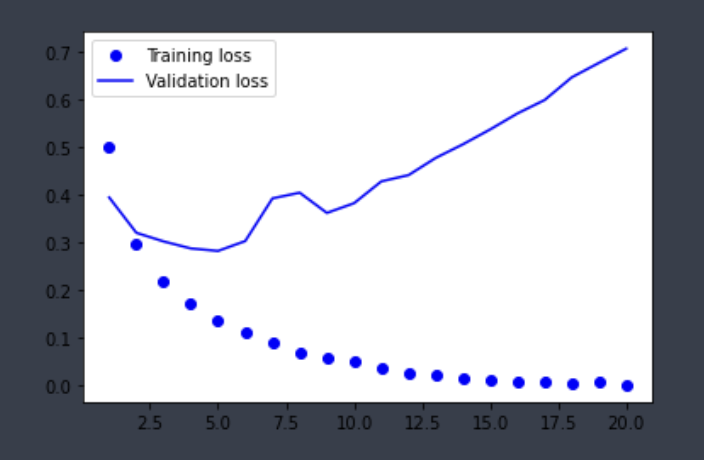
Training_loss는 계속 줄어들며 과최적화되는 모습이다. 검증 셋에서 우리는 epoch이 5정도가 될 때 Validation_loss가 최소임을 확인할 수 있었다. 어쨌든 현재 모델은 과도한 epoch으로 인해 과최적화 되었다고 볼 수 있다.

다중 분류 문제

Reuter datasets를 활용한 다중 분류 (multiclass classification)모델을 만드는 것을 목적으로 한다. 정확히는 단일 레이블 다중 분류 문제이다. 즉, 각 sample이 여러 개의 범주에 속할 수 있다면 다중 레이블 다중 분류 문제이다.

Reuter Datasets info

Metadata	infomation
data_name	Reuter
train_data	samples : 8982
test_data	samples : 2246
labels	46개의 토픽
explain	데이터는 이미 각 단어 시퀀스가 숫자 시퀀스로 변환되어 있음.

IMDB 데이터셋처럼 각 샘플은 정수 리스트이다. 샘플에 연결된 레이블은 토픽의 인덱스로 0과 45사이의 정수이다. 범주형 데이터이기 때문에 원-핫 인코딩하여 레이블을 벡터로 변환한다. 다음은 원-핫 인코딩을 위한 함수이다.

def to_one_hot(labels, dimension=46):
    results = np.zeros((len(labels), dimension))
    for i, label in enumerate(labels):
        results[i, label] = 1
    return results
y_train = to_one_hot(train_labels)
y_test = to_one_hot(test_labels)

이렇게 레이블을 위한 인코딩 함수가 준비되었으며, 우리는 이전 데이터셋에서 처럼 train_data, test_data를 멀티-핫 인코딩하고, train_labels, test_labels를 원-핫 인코딩한다.

이번 문제는 이전 IMDB와 유사하나 출력 클래스 개수가 2에서 46개로 늘어났다. 아직은 정도에 대한 감을 잡지 못하지만, 책에서 일단은 안내를 해주는 것이 중간층의 유닛을 이전과 어떻게 다르게 할 지를 결정해준다. 간단하게는, 이전의 2개의 출력을 고민해야할 때 보다 더 모델을 목잡하게 설계를 해야한다는 것이다. 한 층에서 이전 층의 출력에서 제공한 정보를 충분히 받아들이지 못한다면 일부 정보를 누락하여 정보의 병목이 발생한다. 그러한 이유로 이전 데이터셋 문제보다 더 규모가 큰 층을 사용한다.

• IMDB와 달리 출력층에서 sigmoid가 아닌 softmax를 사용하였다
  https://insomnia.tistory.com/12 (softmax vs sigmoid)
  간단하게는 binary문제에서는 sigmoid를, multiclass문제에서는 softmax를 사용하면 된다.

---

신경망 모델 정의, 및 훈련

model = keras.Sequential([
    layers.Dense(64, activation='relu'),
    layers.Dense(64, activation='relu'),
    layers.Dense(46, activation='softmax'),
])
model.compile(optimizer='rmsprop',
             loss='categorical_crossentropy',
             metrics=['accuracy'])           
history = model.fit(partial_x_train,
                   partial_y_train,
                   epochs=20,
                   batch_size=512,
                   validation_data=(x_val, y_val))

검증

import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.legend()
plt.show()```

---

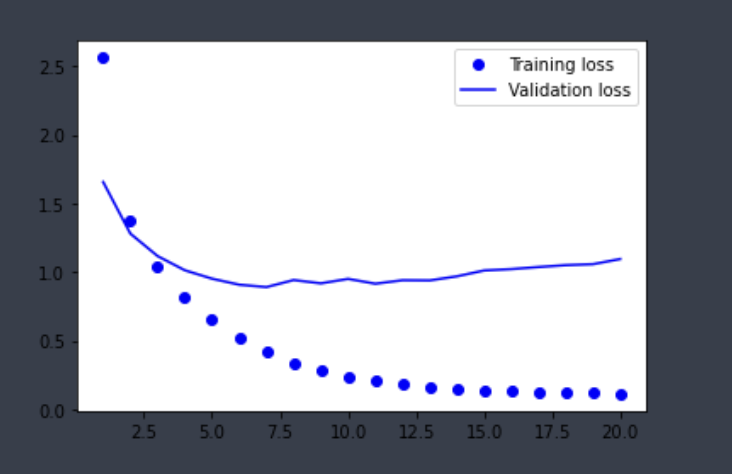
분류 문제 정리

• N개의 클래스로 데이터 포인트를 분류하려면 모델의 마지막 Dense 층의 크기는 N이어야 한다.
• relu 활성화 함수와 함께 Dense층을 쌓은 모델은 여러 종류의 문제에 적용가능 함.
• 이진 분류 문제에서 모델은 하나의 유닛과 sigmoid 활성화 함수를 가진 Dense층으로 끝나야 한다.
• 이진 분류에서의 손실함수는 binary_crossentropy이다.
• rmsprop은 어디서든 좋은 선택
• 항상 훈련 세트 이외의 데이터에서 성능을 모니터링 해야한다.
• N개의 클래스에 대한 확률 분포를 출력하기 위해서는 softmax 활성화 함수 사용
• 분류 문제에서는 항상 범주형 크로스엔트로피를 사용해야함.
• 레이블을 범주형 인코딩으로 인코딩 하고 categorical_crossentrophy 손실함수를 사용
• 레이블을 정수로 인코딩하고 sparse_categorical_crossentrophy 손실함수를 사용
• 많은 수의 범주를 분류할 때 중간층의 크기가 너무 작으면 모델에 병목이 생길 수 있음(성능저하)

회귀문제 : 주택가격예측

앞서 분류문제의 경우에는 입력 데이터 포인트의 개별적인 레이블 하나를 예측하는 것이 목적이다. 회귀문제의 경우에는 개별적인 레이블 대신에 연속적인 값을 예측하는 것이다.

boston_housing Dataset

Metadata	infomation
data_name	boston_housing
train_data	samples : 404
test_data	samples : 102
labels	연속적인 값
explain	입력 데이터에 있는 각 특성의 스케일이 서로 다르다. 어떤 값은 0~1 사이의 값을 , 어떤 값은 1~100사이의 값을 가지기도 한다.

데이터 전처리
상이한 스케일을 가진 값을 신경망에 주입할 경우 문제가 된다. 이런 데이터를 다루기 위해서는 특성별로 정규화가 필요하다. 다음의 코드처럼 평균을 빼고 표준편차로 나누어 feature별로 스케일링을 진행한다.

#정규화 하기
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
test_data -= mean
test_data /= std

모델 설계

def build_model():
    model = keras.Sequential([
        layers.Dense(64, activation='relu'),
        layers.Dense(64, activation='relu'),
        layers.Dense(1)
    ])
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

이 모델의 경우 마지막 층은 하나의 유닛을 가지고 있고 활성화 함수를 부여하지 않는다.(선형 층이라 부른다) 예로 마지막 층에 sigmoid를 적용할 경우 모델이 0과 1사이의 값을 예측하도록 학습 될 것이다. 또한 loss의 경우에도 mse 손실함수를 사용한다. (회귀에 적합) 훈련 성능 지표로는 mae를 사용한다. 예로 mae가 0.5라면 예측이 평균적으로 500달러 정도 차이가 난다는 뜻이다.

데이터 개수가 적을 때
데이터 개수가 적을 때 데이터를 훈련 세트와 검증 세트로 나누게 되면 검증 세트와 훈련 세트로 어떤 데이터 포인트가 선택되었는지에 따라 검증 점수가 크게 달라진다. 이런 상황에서 가장 좋은 방법은 K-fold cross-validation이다.

K-fold cross-validation 적용한 훈련

k=4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
    print(f"#{i}번째 폴드 처리중")
    val_data = train_data[i * num_val_samples: (i+1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i+1) * num_val_samples]
    partial_train_data = np.concatenate(
    [
        train_data[:i * num_val_samples],
        train_data[(i+1) * num_val_samples:]
    ], axis=0)    
    partial_train_targets = np.concatenate(
    [
        train_targets[:i * num_val_samples],
        train_targets[(i+1) * num_val_samples:]
    ], axis=0)    
    model = build_model()
    model.fit(partial_train_data, partial_train_targets,
             epochs=num_epochs, batch_size=16, verbose=0)
    val_mse , val_mae = model.evaluate(val_data, val_targets, verbose=0)
    all_scores.append(val_mae)

k = 4로 설정하였으며 epochs은 100으로 설정하였다. 4겹이기 때문에 우리는 k-fold를 진행하지 않았을 때보다 4배 더 훈련하게 된다. 비용이 올라가지만, 데이터가 적기에 충분히 용인가능하다.

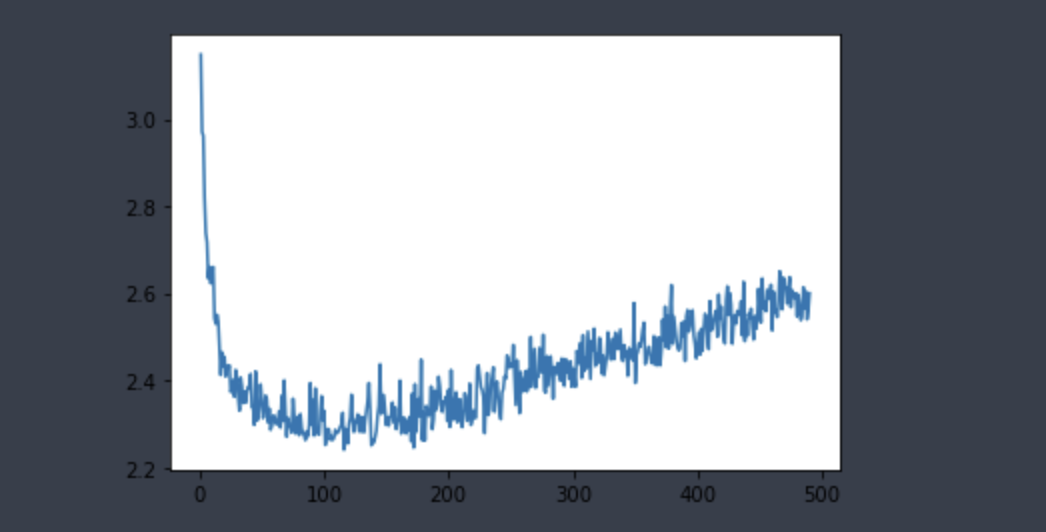
Epochs = 500 으로 최적점 찾기

truncated_mae_history = average_mae_history[10:]
plt.plot(range(1, len(truncated_mae_history) + 1), truncated_mae_history)
plt.show()

검증 MAE가 120~ 140번째 에포크 이후부터 줄어드는 것을 확인 가능. 즉 해당 지점부터는 과대적합이 시작된다는 것을 알 수 있다.