데이터에 대한 접근방법
머신러닝의 근본적인 이슈
최적화(optimaization)와 일반화(generalization) 사이의 줄다리기
- 최적화 : 가능한 훈련 데이터에서 최고의 성능을 얻으려고 모델을 조정하는 과정
- 일반화 : 훈련된 모델이 이전에 본 적 없는 데이터에서 얼마나 잘 수행되는지 의미
데이터의 관점에서
- 불확실한 특성 : 덜 익은 바나나와 익은 바나나의 구분을 가능하게 하는 특성은 무엇인가?
- 드문 특성과 가짜 상관관계 : 드문 특성 값에 대해 무시하지 않고 그것을 반영하는 것은 옳은 일인가? 이렇게 반영했을 때 만들어지는 상관관계는 가짜 상관관계일 확률이 높다.
결론으로는 딥러닝 모델을 향상시키는 가장 좋은 방법은 더 좋고, 더 많은 데이터에서 훈련하는 것이다.
딥러닝의 함정
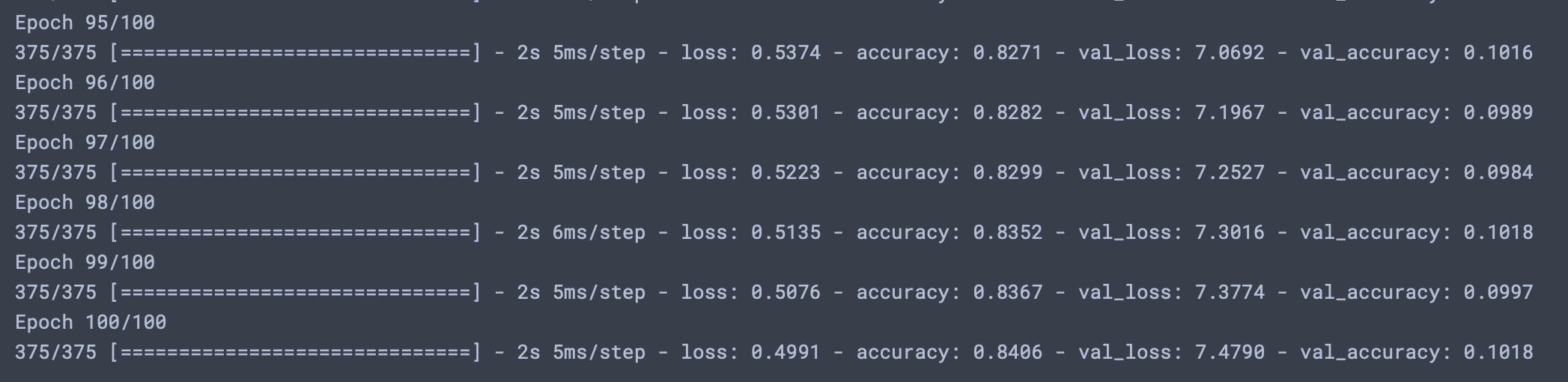
딥러닝 모델에 관한 놀라운 사실중 하나는 표현능력이 충분하다면 어떤 것에도 맞출 수 있도록 훈련할 수 있다는 것이다. 만약 MNIST데이터셋의 레이블을 무작위로 섞은 후 훈련을 진행시킨다면, 입력과 레이블간의 상관성이 랜덤화에 의해 사라졌음에도 훈련이 잘 진행되는 것을 볼 수 있다. 하지만 검증 손실은 시간이 지남에 따라 향상되지 않는다.(아래 구현)
구현
import keras from tensorflow import keras from tensorflow.keras import layers train_images = train_images.astype('float32') / 255 random_train_labels = train_labels[:] # 레이블 다른 변수에 카피 np.random.shuffle(random_train_labels) # 레이블을 랜덤 셔플 model = keras.Sequential([ layers.Dense(512, activation='relu'), layers.Dense(10, activation='softmax') ]) model.compile(optimizer='rmsprop', loss='sparse_categorical_crossentropy', metrics=['accuracy']) model.fit(train_images, random_train_labels, epochs=100, batch_size=128, validation_split=0.2)결과
매니폴드 가설
고차원의 예시가 나타나, 이해가 어려운 부분이긴 하다.
- 매니폴드(manifold)를 형성한다는 것은 어떤 말일까?
책에서는 MNIST데이터, 즉 손글씨 숫자가 28*28 배열로 이루어진 공간에서 매니폴드를 형성한다고 말했다.
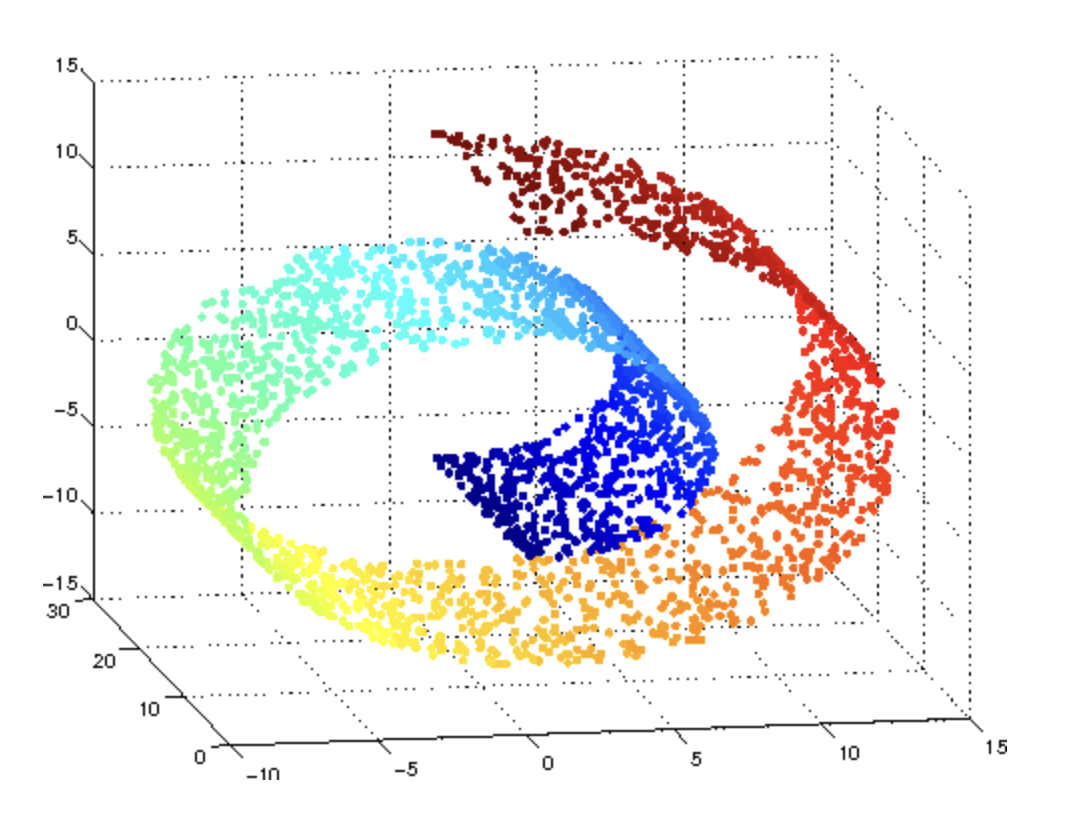
매니폴드 학습
매니폴드 학습은 다음과 같은 스위스롤을 눈을 감고 비유클리디안의 형태를 데이터를 이용하여 손으로 직접 만져가며 형태를 인식해나가는 것이다. 그렇게 되면 최종 학습된 것은 3차원이아닌 2차원이 될 수 있으며, 스위스 롤의 경우에도 신경망입장에서는 펼친 모양으로 이해할 수 있을 것이다.
매니폴드 보간
위와 같은 매니폴드(스위스 롤)중 두 데이터 사이를 보간하는 것이 항상 가능하다. 즉, 연속적인 경로를 따라 한 입력에서 다른 입력으로 변형 할 때 모든 포인트가 이 매니폴드에 속한다.
- 데이터 보간을 통해 딥러닝의 일반화가 달성되지만 이것이 일반화의 전부는 아니다.
머신러닝 모델의 평가
모델 평가의 핵심
가용한 데이터를 항상 훈련, 검증, 테스트 3개의 세트로 나누는 것이다.
- 만약 훈련세트와 테스트세트 2개만 사용한다면 간단해보이지만, 모델은 지속적으로 하이퍼파라미터 튜닝이 이루어지기 때문에 보통은 검증세트에서 모델의 성능을 평가하여 하이파파라미터 튜닝을 수행한다. 이러한 튜닝이 반복적으로 이루어질 경우 모델은 검증세트에 과대적합될 수 있다.
- 일반적으로 데이터가 많을 때는 훈련, 검증, 테스트셋으로 나누어 최적의 모델을 찾고 테스트셋에서 최종 검증을 진행하지만 데이터가 적을때는 K-겹 교차검증 혹은 셔플링 K-겹 교차검증을 사용한다.
- 우리는 검증하고 나온 결과에 대해 이것이 우수한 모습을 보여주는지에 대한 감각이 필요하다. 그렇기 때문에 "상식 수준의 기준점"을 알고 있는 것이 중요하다.
훈련성능 향상법
- 학습률 : 책에서는 1.0 과 0.02로 하여금 학습률의 차이를 두어 훈련성능의 향상을 도모한다.
- 배치크기 : 배치샘플을 더 늘리면 유익하고 잡음이 적은 그레이디언트가 만들어진다.
- 모델용량 : 이전에 우리는 모델의 용량에 관련해서 "병목"이라는 현상을 공부하였다. 데이터에 비해 모델의 용량이 부족하다면 모델의 표현능력이 부족한 것이다.
!중요 : 모델은 항상 과대적합이 가능하다.
일반화 성능 향상법
- 데이터셋 큐레이션 : 잘못된 데이터 셋 안에서 모델의 일반화를 위해 노력하는 것은 의미없는 일일 수가 있다. 데이터가 충분한지, 입력 데이터를 시각화하여 이상치를 확인하고, 데이터를 정제하고 누락된 데이터를 처리하고, feature가 너무 많다면 feature selection으로 하여금 차원을 줄이기도 해야한다.
- 특성 공학 : 모델에 데이터를 주입하기 전에 학습이 아닌 하드코딩된 변환을 적용하여 알고리즘이 더 잘 수행되도록 만들어준다. 일반적으로 최신 딥러닝은 자동으로 원본데이터에서 유용한 특성을 추출할 수 있지만, 특성이 강력하여 신경망 자체가 필요하지 않은 경우가 존재할 수 있다.
- 조기종료 : 잠재 매니폴드를 학습하기 위해 필요한 최소한의 것보다 훨씬 많은 자유도를 가진다. 이전 장에서 보듯 항상 최상의 검증 점수를 내는 에포크 횟수를 찾기 위해 필요보다 오래 모델을 훈련하였다. EarlyStopping 콜백을 사용할 경우 에포크가 끝날 때 마다 모델을 저장하고 최상의 에포크를 찾은 후 저장된 모델을 재사용할 수 있다.
- 규제 : 훈련 데이터에 완벽하게 맞추려는 모델의 능력을 적극적으로 방해하는 일련의 모범사례이다. 모델을 더 간단하고 더 평범하게, 곡선을 부드럽고 더 일반적으로 만드는 경향을 가짐.
규제
- L1 규제 : 가중치의 절댓값에 비례하는 비용이 추가된다.
- L2 규제 : 가중치의 제곱에 비례하는 비용이 추가된다.(가중치 감쇠)
딥러닝 프로젝트에선 보통 L2규제를 자주 이용한다. 가중치 규제는 모델의 복잡도에 제한을 두는 것이다. 즉, L2의 경우 높은 가중치에 대해 제곱이 되므로 높은 가중치는 더욱 높은 값을 가지게 되어 0.002가 곱해져 모델의 전체 손실에 더해진다는 의미이다.
드롭아웃 추가(dropout
모델 층에 드롭아웃을 적용하면, 훈련하는 동안 무작위로 층의 출력 특성을 일부 제외시킨다.(0으로 만든다) 이때 드롭아웃 비율은 출력 벡터에 대해 0이 될 특성의 비율이다. (보통 0.2~0.5)
- 의문 : 이상하고 무계획적으로 보임. 갑자기 랜덤하게 0으로 출력값을 무시한다는 것이 상식적으로 이해가 힘듬.
드롭아웃을 만든 제프리 힌튼은 은행의 부정 행위 예시를 들었다
. 은행에서 부정행위를 하려면 직원들 사이에 유대가 필요하다. 이것을 방지하기 위해 은행은 행원들을 지속적으로 바뀌게끔 시스템화 하였다.
핵심 아이디어는 층의 출력 값에 노이즈를 추가하여 중요하지 않은 우연한 패턴을 깨뜨리는 것이다