다이나믹 프로그래밍

• 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 다시 저장 → 다시 계산하지 않도록 함
• 완전 탐색이 매우 비효율적인 문제에서 시간을 획기적으로 줄일 수 있는 알고리즘
  
  

조건

최적 부분 구조 optimal substructure

큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제를 해결 가능함

중복되는 부분 문제 overlapping subproblem

동일한 작은 문제를 반복적으로 해결해야 함

예시) 피보나치 수열

점화식 : $a_n = a_{n-1} + a_{n-2}, a_1 = 1, a_2 = 1$

단순 재귀 소스코드

def fibo(x):
	if x == 1 or x == 2:
    	return 1
    return fibo(x-1) + fibo(x-2)

1. 최적 부분 구조

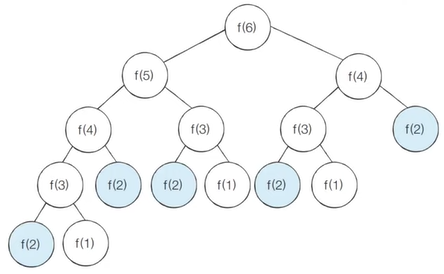
• 큰 문제 f(4)를 해결하기 위해 작은 문제 f(3)와 f(2)를 해결한 결과 값을 가지고 있으면 됨

2. 증복되는 부분 문제

• 재귀 함수 쓰게 되면 f(6)을 해결하기 위해 f(2)가 여러 번 호출되는 것처럼, 중복되는 부분 문제가 존재함
  ⇒ 지수 시간 복잡도 ( $O(2^N)$ )

효율적인 해법: 다이나믹 프로그래밍

Top-Down 하향식

• 구현 과정에서 재귀 함수 이용
• 한 번 계산한 결과를 저장하기 위해 메모이제이션 기법 사용

메모이제이션

• 한 번 계산한 결과를 메모리 공간에 메모하는 기법
• 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져옴
• 값을 기록해놓는다는 점에서 캐싱(Caching)이라고도 함
• 한 번 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미하는 것으로, 다이나믹 프로그래밍에 국한된 개념이 아님

탑다운 다이나믹 프로그래밍 소스코드

d = [0] * 100  # 계산된 결과 메모이제이션 할 리스트를 먼저 초기화
def fibo(x):
	if x == 1 or x == 2:
    	return 1
	if d[x] != 0:  # 이미 계산된 적 있다면
    	return d[x]   # 그대로 반환
    # 계산된 적 없으면 점화식에 따라 계산 후 결과 반환
	d[x] = fibo(x - 1) + fibo(x - 2)  
    return d[x]

메모이제이션 동작 분석

• 색칠된 노드만 처리되는 것을 기대할 수 있음

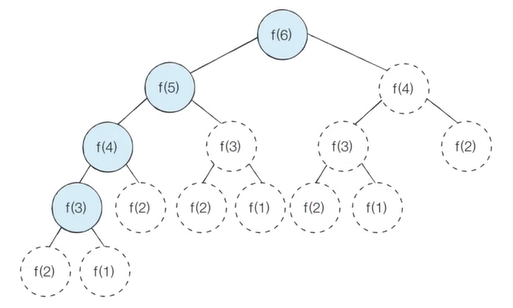
• 메모이제이션 이용시 피보나치 수열 함수의 시간 복잡도: $O(N)$
• fibo(6)을 계산할 때 6 5 4 3 2 1 2 3 4 순으로 호출됨
• 이미 계산된 값은 단순히 d[x]를 불러오는 것이므로
  
  

Bottom-Up 상향식

• 아래서부터 작은 문제를 차례로 해결하는 방식 → 반복문 사용
• 다이나믹 프로그래밍의 전형적 형태
• 결과 저장용 리스트를 DP 테이블이라고 부름

보텀업 다이나믹 프로그래밍 소스코드

d = [0] * 100  # DP 테이블 초기화

# 초기값 선언
d[1], d[2] = 1, 1  # a1, a2
n = 99

# 반복문으로 구현: 점화식 그대로 사용
for i in range(3, n+1):
	d[i] = d[i-1] + d[i-2]

다이나믹 프로그래밍 vs 분할 정복

• 둘 다 최적 부분 구조를 가질 때 사용 가능함
• 차이점은 부분 문제의 중복
  • 다이나믹 프로그래밍 문제에서는 부분 문제가 중복됨
  • 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않음

예시) 퀵 정렬

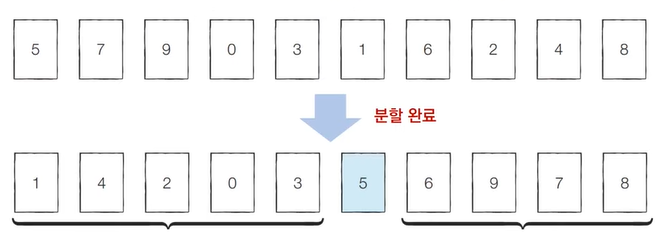
• 분할 정복 대표 예시
• 한 번 피벗이 자리 변경해서 자리 잡으면 그 위치는 바뀌지 않음
• 즉, 분할 이후 해당 피벗 다시 처리하는 부분 문제는 호출되지 않음
  
  

다이나믹 프로그래밍 문제 접근법

유형 파악

• 그리디, 구현, 완전 탐색 등의 아이디어로 해결할 수 있는지 검토
  • 다른 알고리즘으로 풀이 방법이 생각 나지 않거나 시간 복잡도 면에서 비효율적이라면 다이나믹 프로그래밍 고려
• 일단 재귀 함수로 비효율적 완전 탐색 프로그램 작성 후, 작은 문제 → 큰 문제 가능하면 코드 개선하는 방법 사용 가능
• 일반적인 코딩 테스트 수준에서는 기본 유형의 다이나믹 프로그래밍 문제가 출제되는 경우가 많음

---

Source
이코테 2021 다이나믹 프로그래밍