다이나믹 프로그래밍 (예제 + LIS)

예제1) 개미 전사

문제

• 개미 전사는 부족한 식량을 충당하고자 메뚜기 마을의 식량창고를 몰래 공격하려고 한다. 메뚜기 마을에는 여러 개의 식량창고가 있는데 식량창고는 일직선으로 이어져 있다.
  
  
• 각 식량창고에는 정해진 수의 식량을 저장하고 있으며 개미 전사는 선택적으로 약탈하여 식량을 빼앗을 예정이다. 이때 메뚜기 정찰병들은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량창고가 공격받으면 바로 알아챌 수 있다.
  
  
• 따라서 개미 전사가 정찰병에게 들키지 않고 식량창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량창고를 약탈해야 한다.

예시

• 식량 창고 4개가 다음과 같을 때

  1 3 1 5

• 개미 전사가 식량을 얻을 수 있는 경우의 수는 8가지
  

• 개미 전사는 두 번째 식량창고와 네 번째 식량창고를 선택했을 때 최댓값인 총 8개의 식량을 빼앗을 수 있다. 개미 전사는 식량창고가 이렇게 일직선상일 때 최대한 많은 식량을 얻기를 윈한다.
  
  
• 개미전사를 위해 식량창고 N개에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최댓값을 구하는 프로그램을 작성하시오.

문제 조건

문제 해결 아이디어

• 특정 식량 창고에 대해서 털지 안 털지의 여부를 결정하면, 아래의 2가지 경우 중 더 많은 식량을 털 수 있는 경우를 선택하면 됨
  

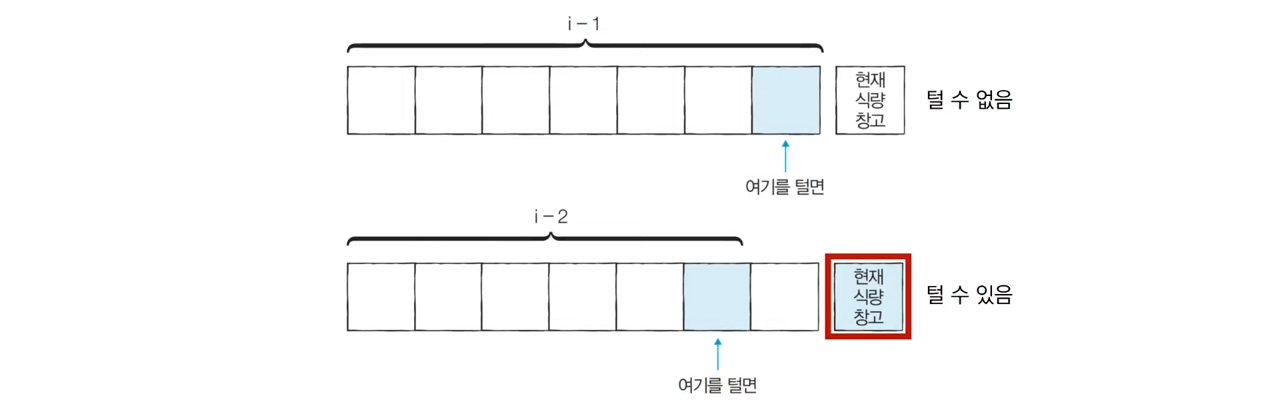
• $i$번째 식량 창고를 털려면 $i-1$번째 식량 창고가 털려있으면 안 되고, $i-2$번째 식량 창고는 털려 있어도 됨

• 따라서 $i$번째 식량 창고까지의 최적의 해는 다음 두 가지 경우 중 큰 값으로 선택 가능

  • $i-1$번째 식량 창고가 털렸을 때의 최적의 해
  • $i-2$번째 식량 창고가 털렸을 때의 최적의 해 + $i$번째 식량 창고의 식량 수

점화식

• $a_i$: $i$번째 식량 창고를 털었을 때 얻을 수 있는 최적의 해(최대로 얻을 수 있는 식량 값)
• $k_i$: $i$번째 식량 창고의 식량 값

$a_i = max(a_{i-1}, \ a_{i-2} + k_i)$

코드

N = int(input())
arr = list(map(int, input().split()))
dp = [0] * 100  

# 다이나믹 프로그래밍 진행(보텀업)
dp[0] = arr[0]
dp[1] = max(arr[0], arr[1])
for i in range(2, N):
    dp[i] = max(dp[i-1], dp[i-2]+arr[i])

print(dp[N-1])

• 강의 한 번 쭉 듣고 내가 짰을 때는 dp[1] = arr[1] 로 초기화 함
  • 문제 조건이 N>=3 이라 상관은 없을 것 같은데
  • dp[1] = max(arr[0], arr[1]) 해줘야 원소 두 개일 때도 최댓값이 나옴
• 소스코드는 dp 길이를 주어진 조건에서 최대로 들어갈 수 있는 수로 초기화해줌
  
  
  

예제 2) 1로 만들기

문제

• 정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.
  
  
  • X가 3으로 나누어 떨어지면, 3으로 나눈다.
  • X가 2로 나누어 떨어지면, 2로 나눈다.
  • 1을 뺀다.
    
    
• 정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

문제 조건

문제 해결 아이디어

• 과정을 도식화하면 다음과 같음
  
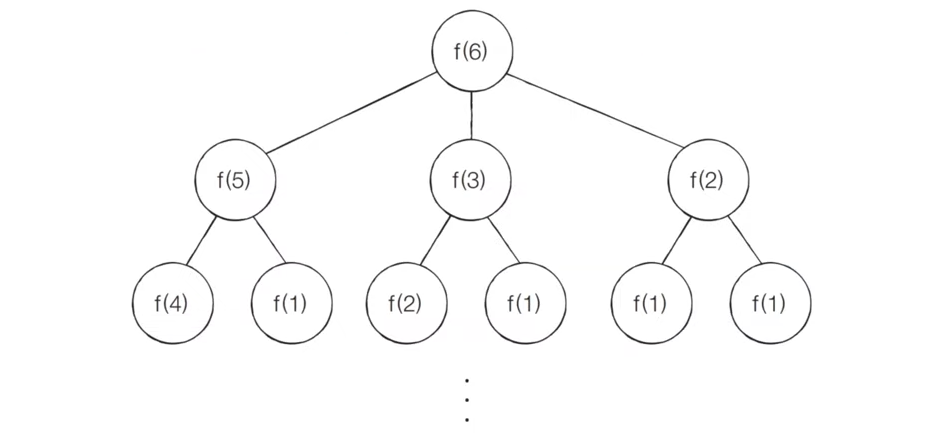
• 최적 부분 구조와 중복되는 부분 문제 만족

점화식

• $a_i$: $i$에서의 최적의 해(최소 연산 횟수)

• $a_i$는 그 이전 단계의 최적의 해 중 최솟값에 1을 더한 값이 될 수 있음

• 이전 단계란, $i$에서 주어진 연산을 수행해 만들 수 있는 모든 경우를 의미함

예시

• $i$ = 6일 때 주어진 연산 중 수행 가능한 경우는

  • 3으로 나눈다 : $i / 3$
  • 2로 나눈다 : $i / 2$
  • 1을 뺀다 : $i - 1$

• 각 경우의 최적의 해

  • $a_{i / 3}$
  • $a_{i / 2}$
  • $a_{i - 1}$

• 따라서 점화식은 다음과 같음

$a_i = min(a_{i - 1}, \ a_{i / 2}, \ a_{i / 3}) + 1$

• 이때, $i - 1$ 항상 수행되지만 $i / 3$ 과 $i / 2$ 은 각각이 가능한 경우에 한해서 수행해야 함

코드

N = int(input())
dp = [0] * 30001
for i in range(2, N+1):
    # 1을 빼는 건 무조건 가능 -> 직전 연산 횟수 + 1를 default로 설정
    dp[i] = dp[i-1] + 1  
    # 3으로 나누어 떨어질 때 dp 값 갱신 가능
    if i%3 == 0:  
        dp[i] = min(dp[i], dp[i//3]+1)  
    # 2로 나누어 떨어질 때 dp 값 갱신 가능
    if i%2 == 0: 
        dp[i] = min(dp[i], dp[i//2]+1) 
print(dp[N])

예제 3) 효율적인 화폐 구성

문제

• N가지 종류의 화폐가 있다.
• 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려고 한다.
• 이때 각 화폐는 몇 개라도 사용할 수 있으며, 사용한 화폐의 구성은 같지만 순서만 다른 것은 같은 경우로 구분한다.
• 예를 들어 2원, 3원 단위의 화폐가 있을 때는 15원을 만들기 위해 3원을 5개 사용하는 것이 가장 최소한의 화폐 개수이다.
• M원을 만들기 위한 최소한의 화폐 개수를 출력하는 프로그램을 작성하시오.

문제 조건

문제 해결 아이디어

• N개의 화폐 종류에 대해 M까지의 수를 확인 → 최대 N*M번 연산
  => 100 x 10000 = 1000000 이므로 1초 안에 가능
• 자연수 $i$ 에서 화폐의 단위 $k$ 를 뺀 $i - k$ 에 대해서도, 주어진 화폐의 단위들로 만들 수 있는 최소의 화폐 개수 $a_{i-k}$가 존재한다면, $a_{i-k}$에 1을 더한 값이 $a_i$의 후보가 될 수 있음
• $a_{i-k}$ 가 존재하지 않는 경우를 챙겨줘야 함

점화식

• $a_i$ : 금액 $i$를 만들 수 있는 최소한의 화폐 개수
• $k$ = 각 화폐의 단위

각 화폐 단위인 k를 하나씩 확인하며

• $a_{i-k}$를 만드는 방법이 존재하는 경우: $a_i = min(a_i,\ a_{i-k}+1)$
• $a_{i-k}$를 만드는 방법이 존재하지 않는 경우: $a_i = INF$

예시

N = 3, M = 7, 화폐의 단위 2, 3, 5

Step 0

• 각 인덱스에 해당하는 값으로 INF(무한)의 값을 설정
• 최소의 수를 찾아야 하는 문제에서, INF로 설정한다는 것은 해당 경우가 가능하지 않다는 의미를 가짐
• 이 문제에서 INF는 특정 금액을 만들 수 있는 화폐 구성이 가능하지 않다는 의미
• M의 최댓값 10,000에 대해서 가질 수 있는 가장 큰 화폐의 개수는 화폐 단위가 1일 때의 값 10,000이므로 INF는 10,001로 초기화
  

Step 1

• 첫 번째 화폐 단위 2를 확인
• $a_4 = min(a_4, \ a_{4-2} + 1)$에서, $a_2$를 만드는 방법이 존재하고 Step0의 $a_4$는 INF이므로 $a_2 + 1$가 되지만,
• $a_7$의 경우 $a_5$를 만드는 방법이 존재하지 않으므로 그대로 INF인 것 확인
• 점화식에 따라 리스트 갱신
  

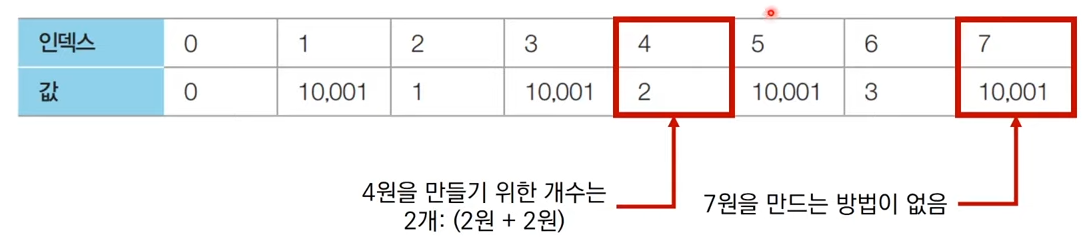
Step 2

• 두 번째 화폐 단위 3을 확인
• $a_7 = min(a_7, \ a_{7-3} + 1)$에서 $a_4=2$ 이므로 $a_7=3$으로 갱신된 것 확인
• 점화식에 따라 리스트 갱신
  

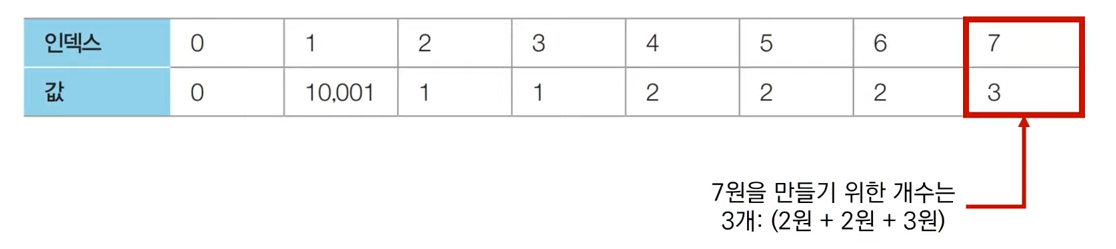
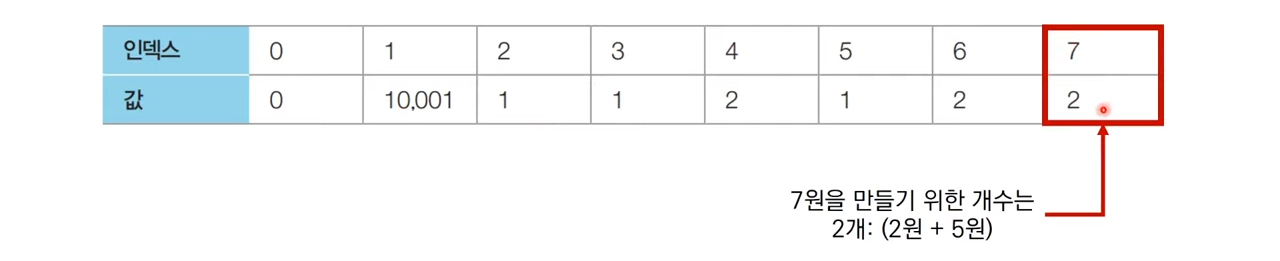
Step 3

• 마지막 화폐 단위 5를 확인
• $a_7 = min(a_7, \ a_{7-5} + 1)$에서 $a_7=3$이고 $a_2=1$로 존재하여 $a_2+1=2$ 이므로 $a_7=2$로 갱신된 것 확인
• 점화식에 따라 최종적으로 리스트 갱신
  

코드

N, M = map(int, input().split())
arr = [int(input()) for _ in range(N)]
dp = [10001] * (M+1)  # inf로 초기화
dp[0] = 0 

for i in range(N):   # N개의 화폐 단위에 대해서
    k = arr[i]
    for j in range(k, M+1):  # i보다 큰 M 이하 자연수에 대해서
        if dp[j - k] != 10001:  # dp[j-k] 존재하면
            dp[i] = min(dp[j], dp[j-k]+1)  # 리스트 갱신 가능

if dp[-1] == 10001:
    print(-1)
else:
    print(dp[-1])

• 주석 달기 편하려고 k = arr[i] 한 거, 생략 가능
  
  

예제 4) 금광

문제

• n x m 크기의 금광이 있다. 금광은 1 x 1 크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있다.
• 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작한다. 맨 처음에는 첫 번째 열의 어느 행에서든 출발할 수 있다.
• 이후에 m - 1번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 한다.
• 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력하는 프로그램을 작성하시오.
  

문제 조건

문제 해결 아이디어

• 현재 위치로 오는 방법은 왼쪽 위, 왼쪽, 왼쪽 아래에서 오는 방법이 있음
• 세 가지 경우 중 가장 많은 금을 가지고 있는 경우로 테이블 갱신

점화식

• $\rm{array}_{\it{i, j}}$ : $i$행 $j$열의 금 개수(입력)
• $\rm{dp}_{\it{i, j}}$ : $i$행 $j$열까지의 최적의 해(최대로 얻을 수 있는 금 개수)

$\rm{dp}_{\it{i, j}} = max(\rm{dp}_{\it{i-1, j-1}},\ \rm{dp}_{\it{i-1, j}},\ \rm{dp}_{\it{i-1, j+1}} ) + \rm{array}_{\it{i, j}}$

• 단, 인덱스가 범위를 벗어나지 않는지 체크
• 편의상 array 테이블을 별도로 두지 않고, dp 테이블을 입력 데이터로 초기화해 갱신하도록 코딩

코드

T = int(input())

for case in range(T):
    N, M = map(int, input().split())
    arr = list(map(int, input().split()))
    dp = []  # dp 테이블 초기화
    idx = 0
    for i in range(N):
        dp.append(arr[idx : idx+M])
        idx += M

    # 다이나믹 프로그래밍
    for j in range(1, M):  # 항상 왼쪽에서 오니까 열부터
        for i in range(N):
            # left_up 정의
            if i == 0:  # 왼쪽 위에서 오는 게 불가능하면
                left_up = 0
            else: 
                left_up = dp[i-1][j-1]
            # left_down 정의
            if i == N-1:
                left_down = 0
            else:
                left_down = dp[i+1][j-1]
            left = dp[i][j-1]
            dp[i][j] += max(left, left_up, left_down)
    result = 0
    for i in range(N):
        result = max(result, dp[i][M-1])
    print(result)

예제 5) 병사 배치하기

문제

• N명의 병사가 무작위로 나열되어 있으며, 각 병사는 특정한 값의 전투력을 보유하고 있다.
• 병사를 배치할 때는 전투력이 높은 병사가 앞쪽에 오도록 내림차순으로 배치를 하고자 한다. 다시 말해 앞쪽에 있는 병사의 전투력이 항상 뒤쪽에 있는 병사보다 높아야 한다.
• 또한 배치 과정에서는 특정한 위치에 있는 병사를 열외시키는 방법을 이용한다.
• 그러면서도 남아있는 병사의 수가 최대가 되도록 하고 싶다.

예시

• N=7일 때 나열된 병사들의 전투력이 다음과 같다고 가정.
  
• 이 때 3번 병사와 6번 병사를 열외시키면, 다음과 같이 남아있는 병사의 수가 내림차순의 형태가 되며 5명이 되고, 이는 남아있는 병사의 수가 최대가 되도록 하는 방법
  

• 병사에 대한 정보가 주어졌을 때, 남아있는 병사의 수가 최대가 되도록 하기 위해서 열외해야 하는 병사의 수를 출력하는 프로그램을 작성하시오.

문제 조건

문제 해결 아이디어

가장 긴 증가하는 부분 수열(Longest Increasing Subsequence, LIS)

• 전형적인 다이나믹 프로그래밍 문제의 아이디어
• [4, 2, 5, 8, 4, 11, 14]에 대해 가장 긴 증가하는 부분 수열은 [4, 5, 8, 11, 15]
• $\rm{D}_{\it{i}}$ : $array[i]$를 마지막 원소로 가지는 부분 수열의 최대 길이

점화식

모든 $O <= j < i$에 대하여, $D[i] = max(D[i],\ D[j]+1) \ \ \rm{if} \ \ \it{array[j] < array[i]}$

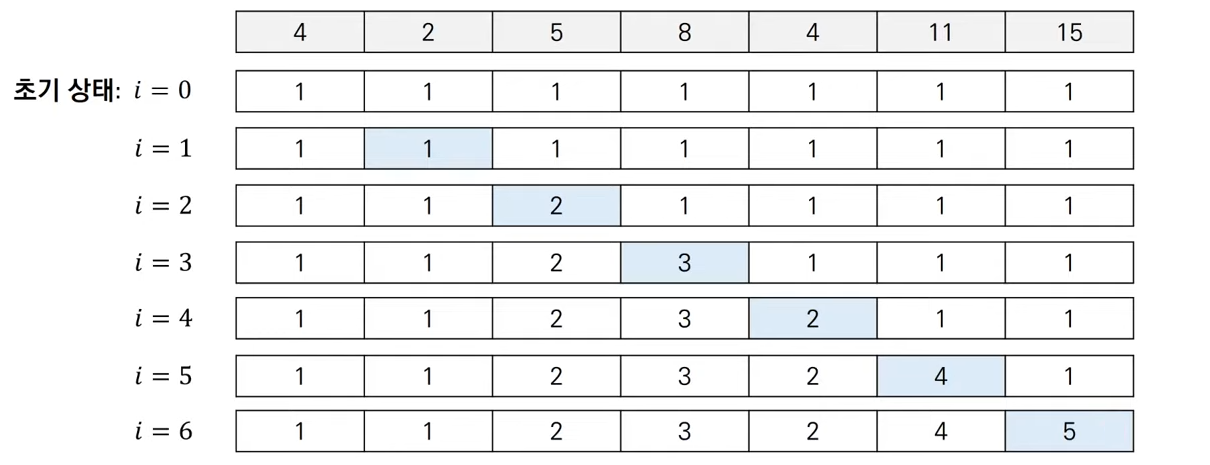
이 문제는 가장 긴 감소하는 부분 수열을 찾는 문제로 치환 가능 → LIS 알고리즘 조금 수정해 적용 가능

입력 받은 병사 정보를 뒤집어 LIS 알고리즘 수행

코드

N = int(input())
arr = list(map(int, input().split()))
# 순서 뒤집어서 '최장 증가 부분 수열' 문제로 변환
arr.reverse()

dp = [1] * N

for i in range(1, N):
    for j in range(0, i):
        if arr[j] < arr[i]:
            dp[i] = max(dp[i], dp[j]+1)

# 열외해야 하는 병사의 최소 수를 출력
print(N - max(dp))

---

Source
이코테 2021 다이나믹 프로그래밍