기하분포(Geometric Distribution)

• Bernoulli trial(베르누이 실험) 에 기반한 분포
• Bernoulli trial은 0과 1의 값이 나오는 실험

정의

첫번째 성공이 일어날때까지 필요한 시행 횟수

Expectation, Variance

예제

음이항분포(Negative Binomial Distribution)

• 기하분포의 일반적인 버전이라 할수 있다.
• 확률함수는 이항분포와 비슷하여 이런 이름을 지닌다.
• 베르누이 시행에 기초한 분포

정의

K번째 성공을 보기 위해 몇번 시행을 해야 하는지

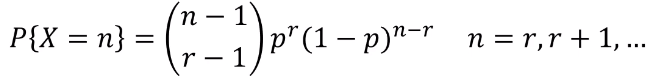
총 r번째 성공을 보기 위해서 n번의 시행이 필요할 확률

그래프 모양

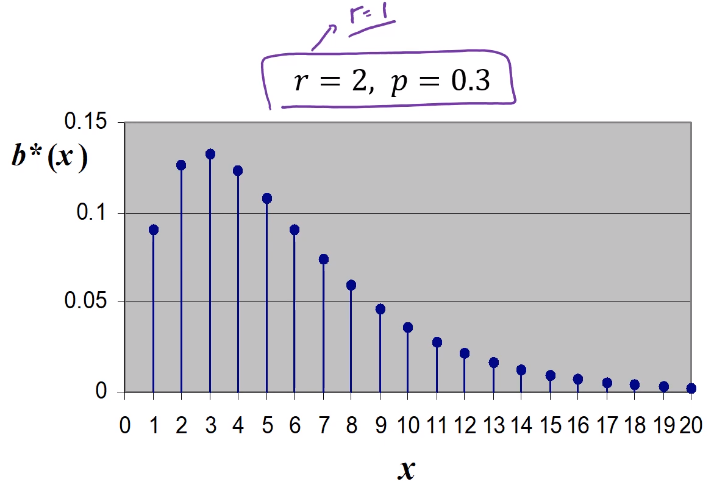
r = 1일때 기하분포와 같아진다.

모수는 r 과 p

기대값, 분포

중요 포인트

모든 확률 변수의 기대값과 분산은 해당 확률함수의 parameter의 함수꼴로 표현이 된다

예제

초기하분포(Hypergeometric Distribution)

• 제조업체에서 품질검사에서 많이 쓰임
• 샘플링한 n개 중에 불량률이 몇개인지에 대한 확률을 구할때 쓰임

정의

샘플링한 n개중에 흰색공의 갯수

• 비복원추출을 기반으로 샘플링 한다.
  

모수

N: 총 공의 갯수
n: 샘플링한 공의 갯수
m: 관심있는 공의 갯수

그래프 모양

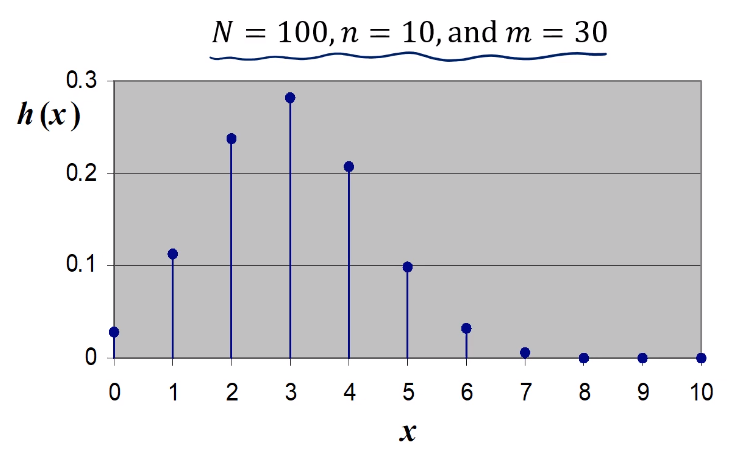
기대값, 분포

예제

지금까지 용어정리

표본공간 추가사항: 실험으로 부터 얻은 모든 결과들의 집합