RNN

1. Model Diagram

Recurrent Neaural Network

보통의 딥러닝에서 퍼셉트론의 구조(Diagram)

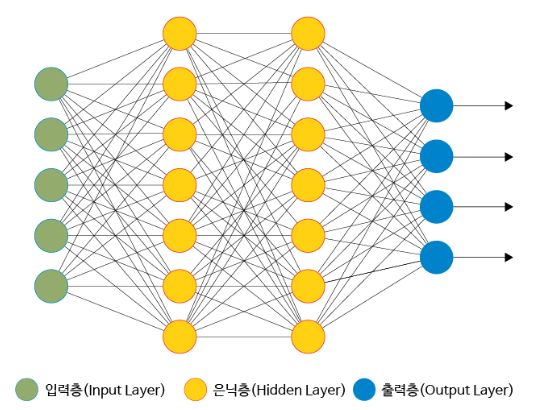
(여러 입력층 -> 은닉층 -> 여러 출력층)

RNN의 퍼셉트론의 구조(Diagram)

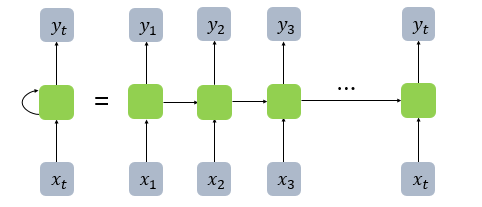
(하나의 입력층 -> 은닉층 -> 하나의 출력층 -> 반복)

수식

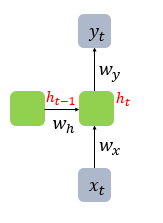
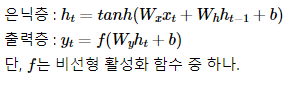
4. 예제

예시문제를 해결해 보는 RNN모델을 생각해보자.

1) 방법1

먼저 RNN의 기본적인 IDEA를 가지고 처음부터 끝까지 구현해 보자.

---

import torch.nn as nn

class RNN(nn.Module):
  def __init__(self, input_size, hidden_size, output_size):
    super(RNN, self).__init__()

    self.hidden_size = hidden_size
   
    self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
    self.i2o = nn.Linear(input_size + hidden_size, output_size)
    self.softmax = nn.LogSoftmax(dim=1)
 
  # 이 경우 hidden cell을 반복적으로 입력받도록 구현해야 하므로 
  # hidden또한 return값에 포함해야 한다.
  def forward(self, input, hidden):
    combined = torch.cat((input, hidden), 1)
    hidden = self.i2h(combined)
    output = self.i2o(combined)
    output = self.softmax(output)
    return output, hidden

  def initHidden(self):
    return torch.zeros(1, self.hidden_size)

---

import torch.optim as optim

n_hidden = 128 
rnn = RNN(n_letters, n_hidden, n_categories)
learning_rate = 0.005 
criterion = nn.NLLLoss()
optimizer = optim.SGD(rnn.parameters(), lr = learning_rate)

def train(category_tensor, name_tensor):
  hidden = rnn.initHidden()
  rnn.zero_grad()

  for i in range(name_tensor.size()[0]):
    output, hidden = rnn(name_tensor[i], hidden)
 
  loss = criterion(output, category_tensor)

  # 학습 (w = w - learning_rate * gradient)
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

  return output, loss.item()

  ##### optimizer.step()의 경우 다음과 같이 사용할 수 있다.#####
  #                                                       #
  # loss.backward()                                       #
  # for p in rnn.parameters():                            #
  #   p.data.add_(p.grad.data, alpha=-learning_rate)      #
  #                                                       #
  #########################################################

2) 방법2

이 방법은 Pytorch library에 존재하는 nn.RNN을 이용해 방법1과 똑같이 작동하는 모델을 구현해 보는 방식이다.

---

# RNN모델 구현(2번 -> nn.RNN사용)
import torch.nn as nn

class RNN(nn.Module):
  def __init__(self, input_size, hidden_size, output_size, num_layers):
    super(RNN, self).__init__()

    self.hidden_size = hidden_size
    self.input_size = input_size
    self.num_layers = num_layers
    self.output_size = output_size

    self.rnn = nn.RNN(input_size, hidden_size, num_layers)
    self.fc = nn.Linear(hidden_size, output_size)

  def initHidden(self):
    return torch.zeros(self.num_layers, 1, self.hidden_size)
 
  def forward(self, input):
    hidden = self.initHidden()
    output, _ = self.rnn(input, hidden)
    output = output[-1]
    output = self.fc(output)
    output = nn.LogSoftmax(dim=1)(output)
    #output = output.reshape(-1)
    return output

---

import torch.optim as optim

n_hidden = 128     # hidden의 출력층 크기
rnn = RNN(n_letters, n_hidden, n_categories, 2)

learning_rate = 0.005                                          # learning rate
criterion = nn.NLLLoss()                                       # nn.LogSoftmax에 가장 적합한 손실함수
optimizer = optim.SGD(rnn.parameters(), lr = learning_rate)   # Gradient Descent의 방법으로 SGD Optimzer 사용 

def train(category_tensor, name_tensor):
  hidden = rnn.initHidden()
  rnn.zero_grad()
  output = rnn(name_tensor)
  loss = criterion(output, category_tensor)
 
  optimizer.zero_grad()
  loss.backward()

  # 학습 (w = w - learning_rate * gradient)
  optimizer.step()

  return output, loss.item()

---

(참고로, nn.RNN과 nn.RNNCell은 차이가 존재하므로 사용에 주의한다.)

LSTM

GRU