DP2
앞서 보았던 dp문제들은 dptable을 채우는 방식이 단순했다.
즉, 위에서 아래, 왼쪽에서 오른쪽과 같이 일정한 방향이 존재했다는 것이다.
dp2에서는 좀 더 복잡하고, 다양한 방식으로 dptable을 결정하는 방법을 알아볼 것이다.
1. TSP
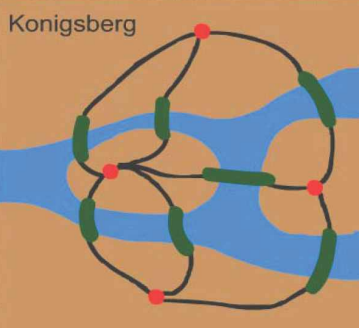
정해진 정점에서 모든 정점을 한번씩만 거쳐서 출발한 정점으로 다시 돌아오는 경로의 최단 거리를 계산하는 문제이다.
(Traveling Salesperson Problem의 약자로,
"해밀턴 경로 구하기", "일주여행 경로 구하기" 라고도 불리는 문제이다.)
1) 아이디어
가장 간단한 방법, 즉 모든 경우의 수를 고려해 본다고 생각해보자. 이 경우 i개의 모든 노드를 순서에 맞춰 줄세우는 방법만 생각해 보더라도
O(n!)의 Time Complexity를 갖는 것을 알 수 있다.
Intro
다른 문제들과는 다르게 이 문제는 출발점과 도착점이 같기 때문에, 평소와 같이 Subproblem을 나누는 기준을 생각하면 잘 풀리지 않을 것이다.
즉, 이 문제의 경우에는 출발점을
v1으로 두는 것이 아니라vi라고 두고,
vi에서 어떤 점들을 지나v1으로 가는 길을 구하는 문제로 바꾸어 보자.
1. 부분 문제로 나눠보기
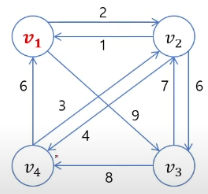
위와 같은 4개의 노드
v1,v2,v3,v4를 가지고 생각해 보자. 이때, 출발점은v1이다.이 문제를 앞의 Intro에서 설명했던 것을 참고하여 어떤 것을 기준으로 Subproblem으로 나눌지 고민해 보자.
흔히 생각할 수 있고, 우리에게 익숙한 기준은 "i에서 1까지 가는데 사용할 노드의 범위"이다.
즉,vi에서 출발해v2~vx를 모두 사용하여v1까지 가는데 드는 비용을 계산하는 것이다.하지만 위의 방법은 Subproblem의 기준에 어긋난다는 것을 확인할 수 있다.
v2~vx를 고려한 결과로v2~vx+1에 대한 결과를 유도할 방법이 없기 때문이다.이 문제의 경우에는 독특하게 Subproblem의 기준을 "i에서 1까지 가는데 사용할 노드의 개수"로 설정해야 한다.
(정확히는 노드의 집합)
vi에서 3개의 Node를 지나 v1으로 가는 최단거리vi에서 2개의 Node를 지나 v1으로 가는 최단거리vi에서 1개의 Node를 지나 v1으로 가는 최단거리vi에서 0개의 Node를 지나 v1으로 가는 최단거리이렇게 나눌 경우 2개를 지나는 경우의 결과를 사용해 3개를 지나는 경우를 유도할 수 있게 된다.
2. DP Table 정의
3. 복잡도 분석
- 시간복잡도:
O(n^2 * 2^n)- 공간복잡도:
O(n * 2^n)
최단경로 알고리즘
1. Floyd-Warshall
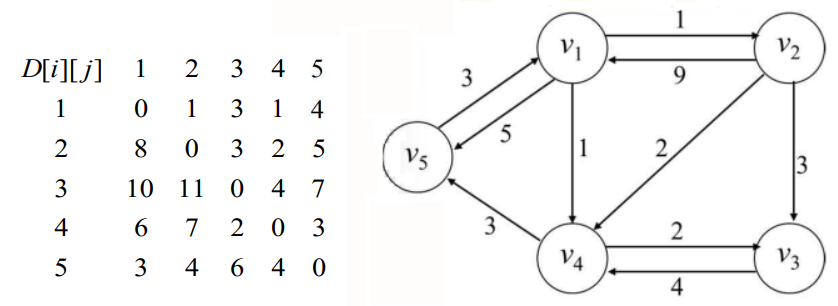
어떤 그래프가 주어졌을 때, 모든 정점에서 다른 정점까지의 최단 거리를 모두 구하는 알고리즘이다.
1) 아이디어
1. 부분 문제로 나눠보기
이 문제는 모든 노드에서 다른 모든 노드까지의 최단 거리를 구하는 문제이다. 즉, i에서 j까지의 최소 거리를 모두 구해야 한다.
이제 이 문제를 Subproblem으로 어떻게 나누어야 하는지 고민해 보자.
우선 이 Subproblem으로 나누는 기준을 "i에서 j까지 가는데 필요한 노드의 범위"라고 생각해 보자.
즉, i에서 j까지 가는데v1~vk의 노드만 고려한다고 생각하는 것이다.이 때,
v1~vk를 기준으로 나눈 결과를 활용해v1~vk+1를 기준으로 나눈 결과를 구성할 수 있으면 Subproblem으로 잘 나눴다고 할 수 있을 것이다.잘 생각해 보면
v1~vk+1만 고려해 i부터 j까지 가는 경우는vk+1을 거치는 경우와 거치지 않는 경우로 나눌 수 있다.
먼저, 거치지 않을 경우의 최소 비용은v1~vk를 기준으로 나눈 결과와 같을 것이고,
거칠 경우의 최소 비용은 i에서v1~vk를 고려해vk+1까지 간 경우에vk+1에서v1~vk를 고려해 j까지 간 경우를 더한 결과와 같을 것이다.즉, SubProblem으로 나누어 진다는 것을 확인할 수 있다.
2. DP Table의 정의

한번 만들어진 dp table을 특정 조건을 고려해 지속적으로 수정하도록 구현할 수도 있다.
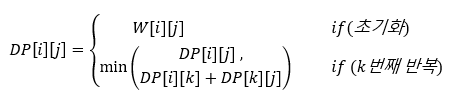
2) Code
int dp[100][100]; int weight[100][100]; int path[100][100] void floyd(int n) { int i, j, k; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) dp[i][j] = weight[i][j]; for (int k = 1; k <= n; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (dp[i][k] + dp[k][j] < dp[i][j]) dp[i][j] = dp[i][k] + dp[k][j]; // path[i][j] = k; }
void find_path(int start, int end) { if (path[start][end] != 0) { find_path(start, path[start][end]); cout << " v" << path[start][end] << " ->"; find_path(path[start][end], end); } }
Time Complexity: O(n^3)
2. Dijkstra
3. Bellman Ford
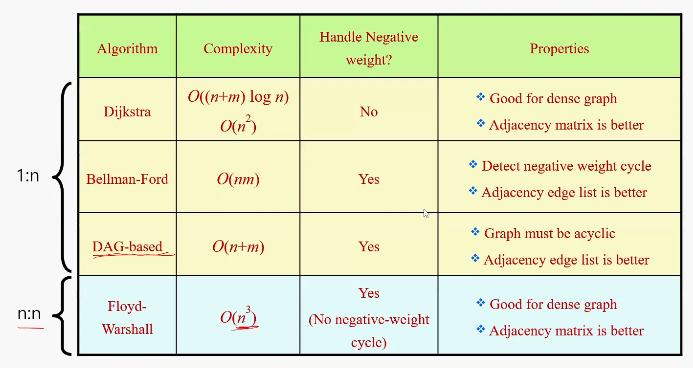
최단경로 알고리즘 비교