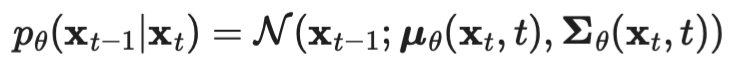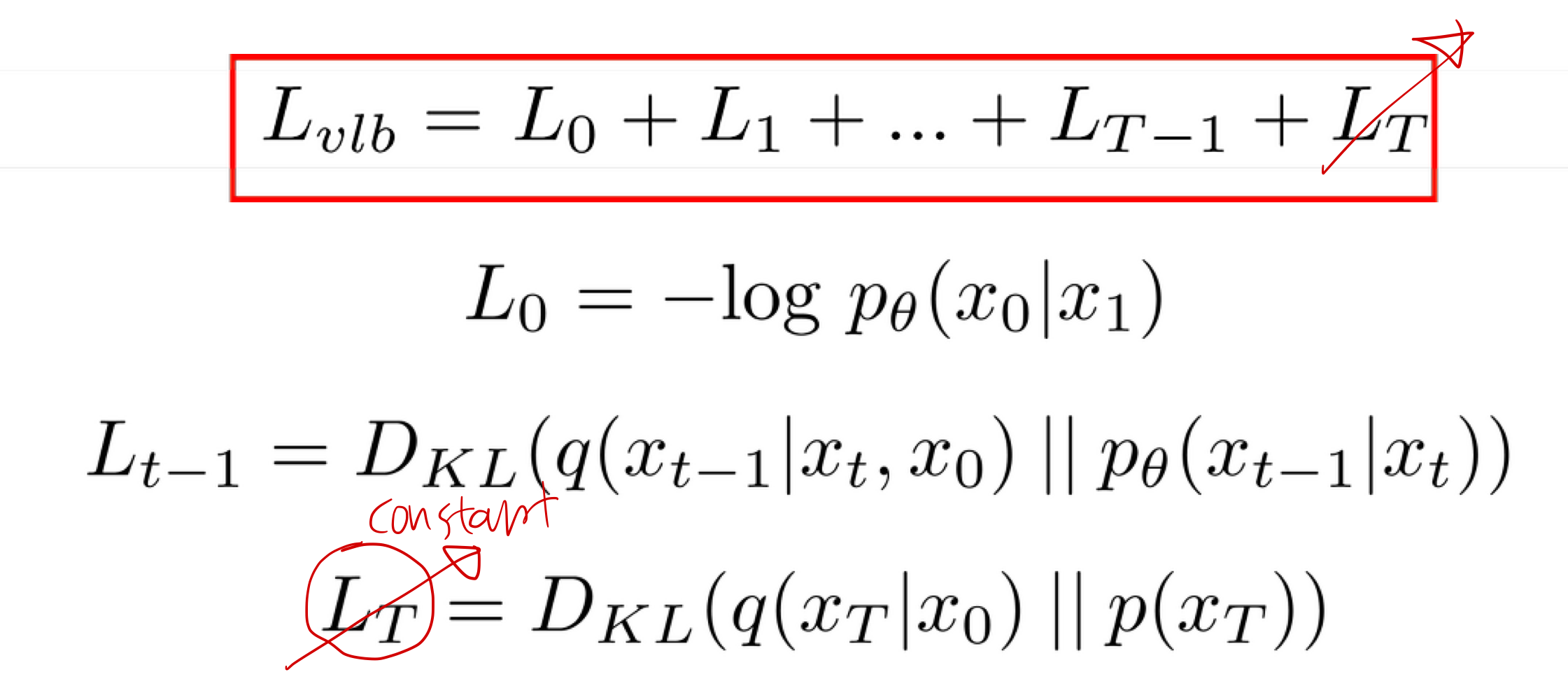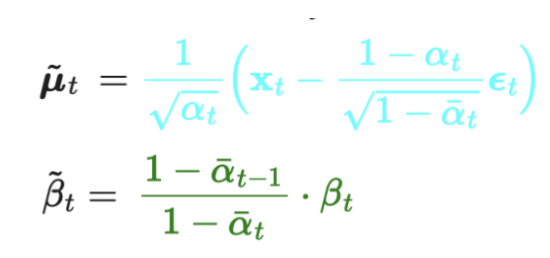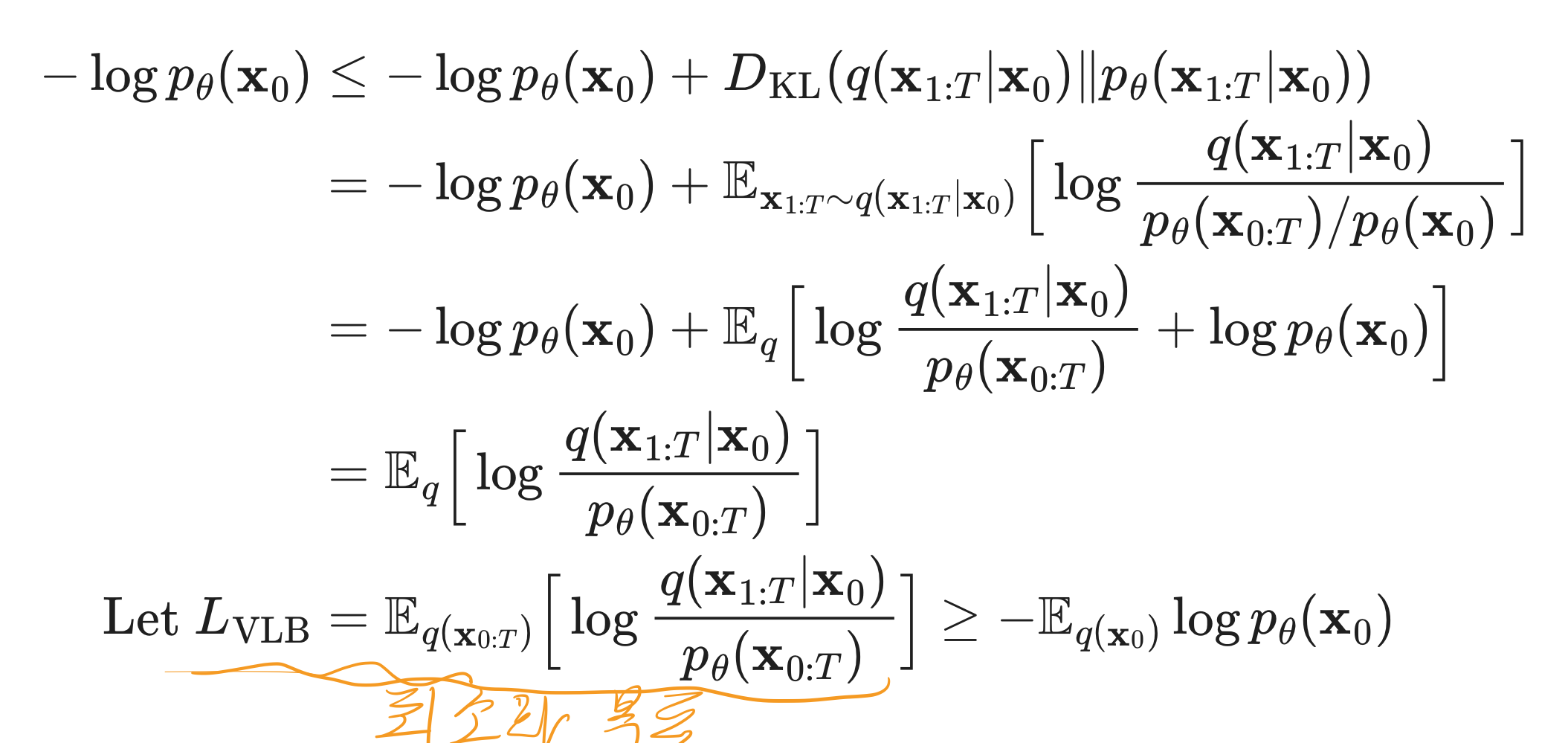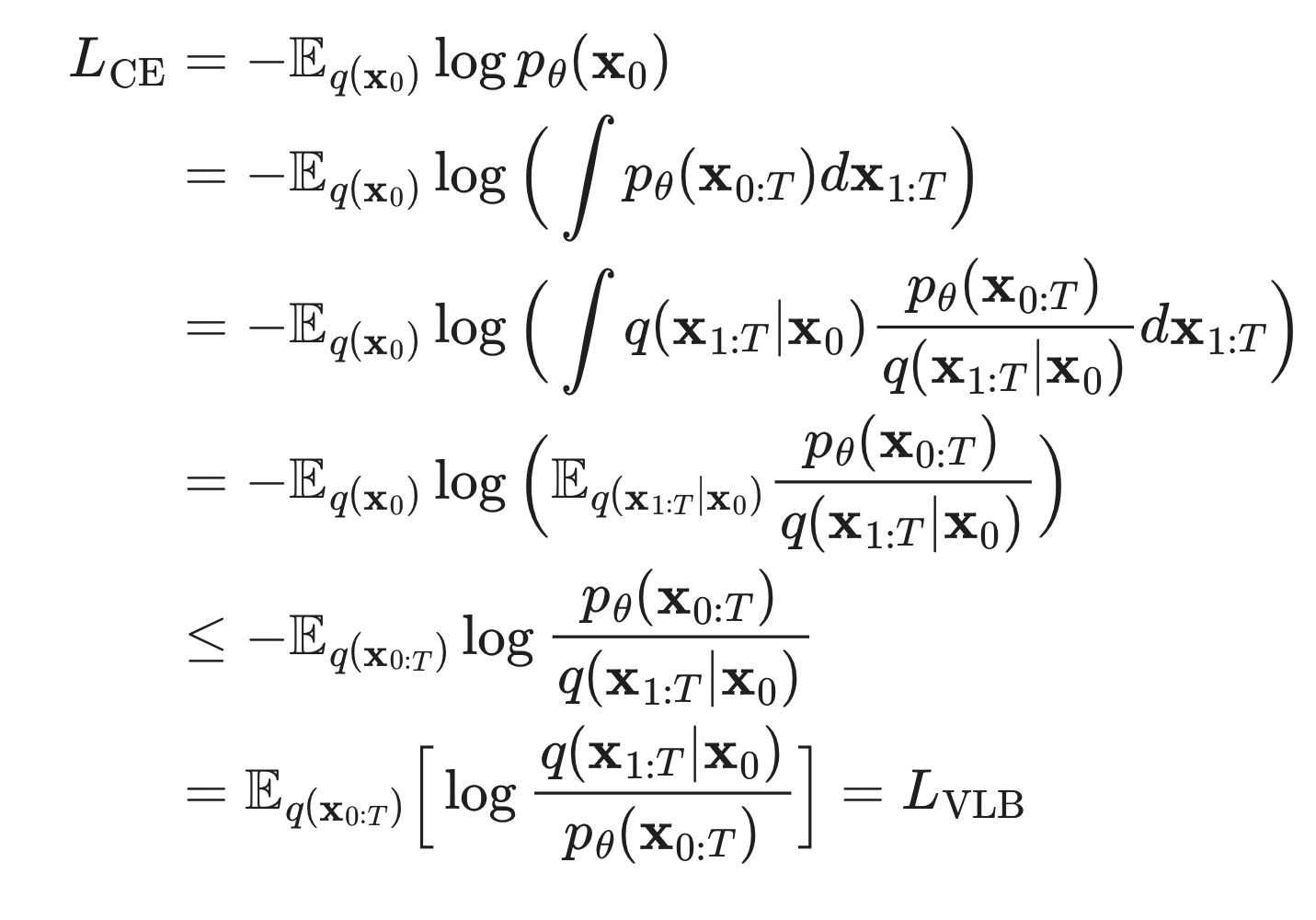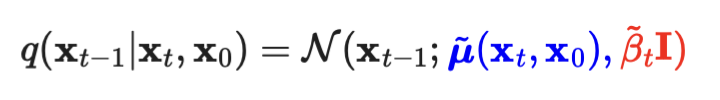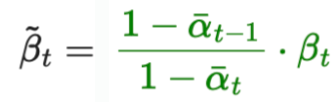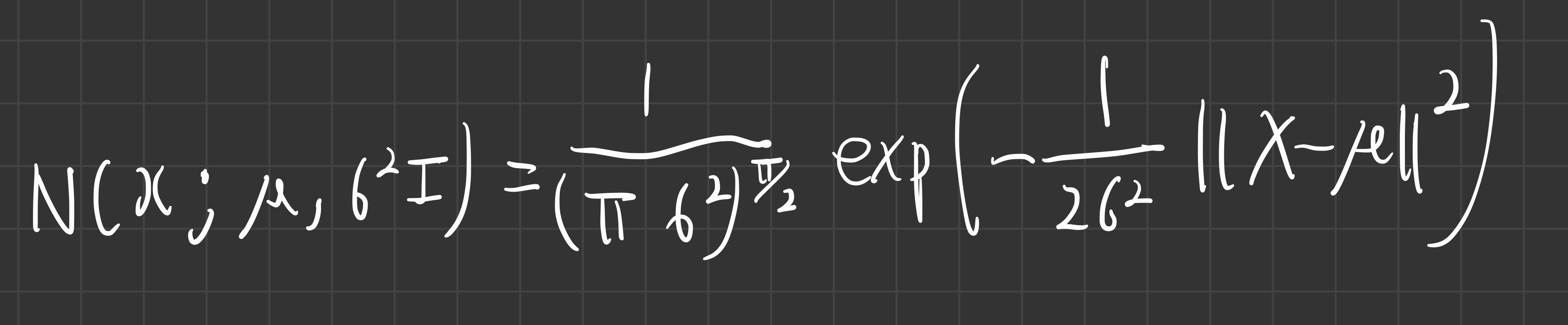DDPM : Denoising Diffusion Probabilistic Models

ad_official·2024년 12월 2일

diffusion

목록 보기

1/12

1. diffusion 큰그림 먼저보자.

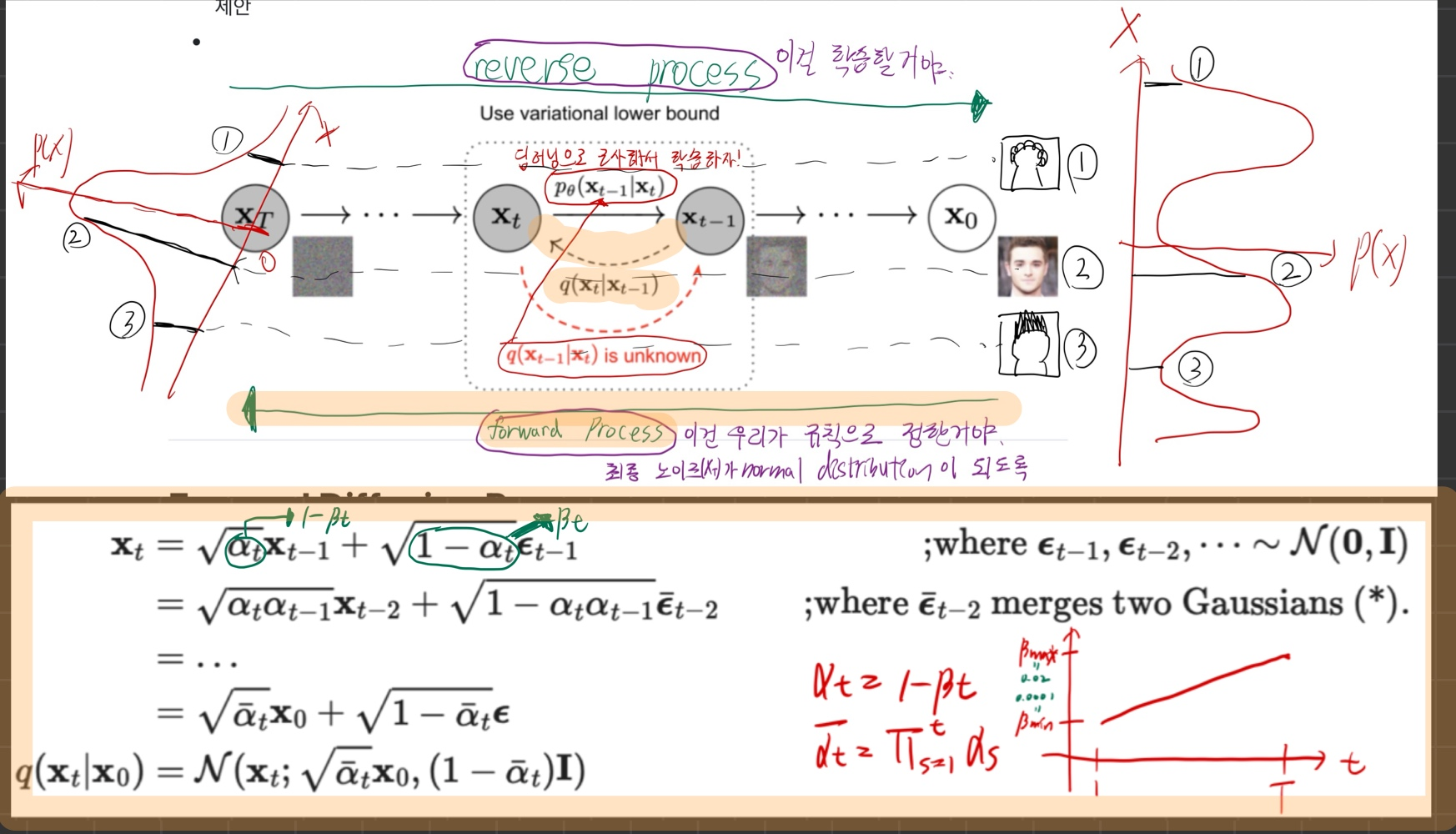
위 그림에서 forward process는 우리가 규칙으로 정한겁니다.
- T는 guassian noise 이미지( $X_T$ )로 만들기 위해 노이즈를 주는 총 단계의 수 입니다. (hyperparameter)
- noise를 주는 방법은 위 그림의 노란색 박스에 명시되어 있습니다.
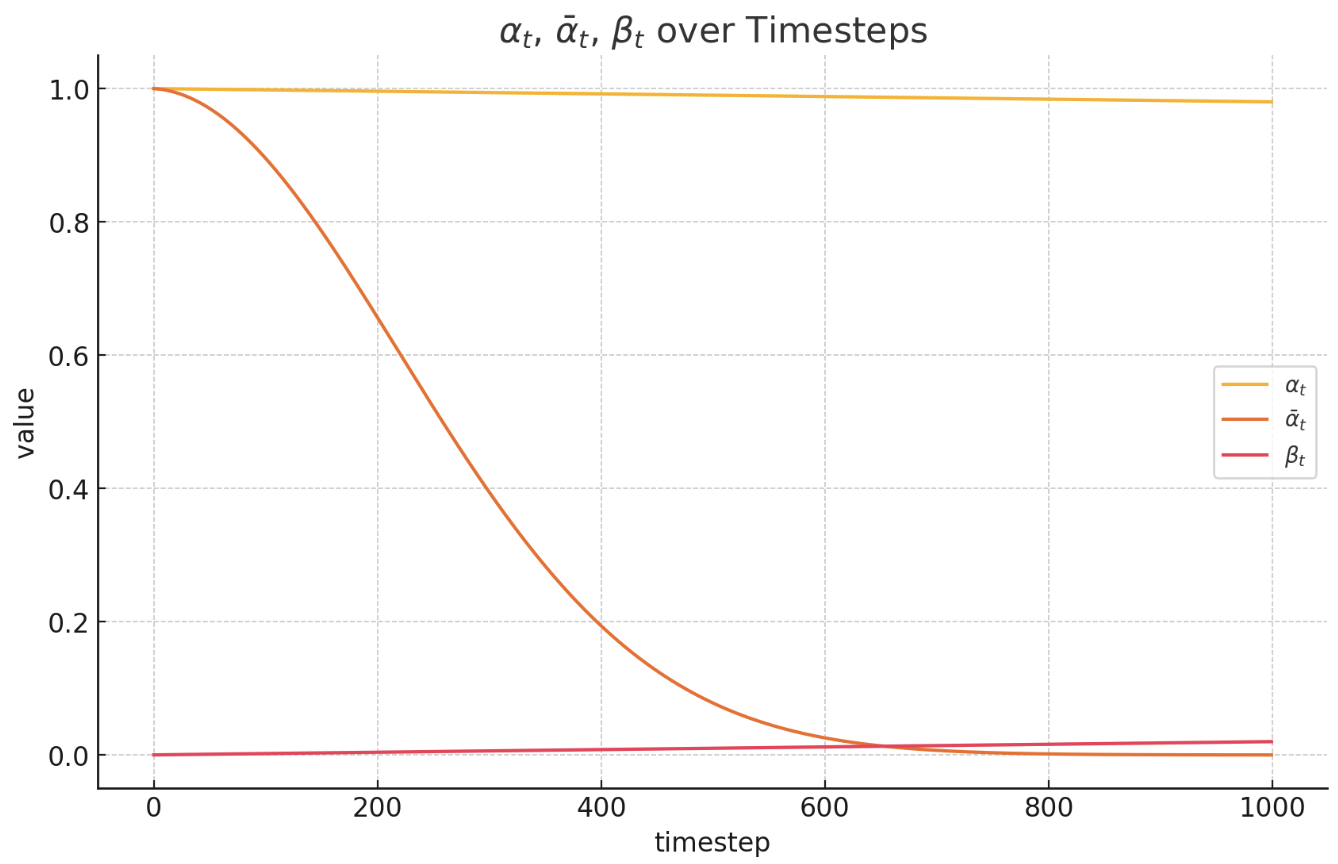
- 어떤 이미지를 noise 화 하건 (1번 이미지, 2번 이미지, 3번 이미지), 알파 베타 스케쥴은 똑같습니다.
- 위 그림에서 $\epsilon$ 은 (1번 이미지, 2번 이미지, 3번 이미지) 마다 랜덤하게 매번 sampling 합니다.
- 위 노란색 박스 수식에 따르면, 우리는 $x_0$ 에서 $x_t$ 까지 noise를 주입할 때, $x_0$ -> $x_1$ -> ... -> $x_t$ 를 거치지 않고도, (동등한 noise화 과정인)
  - $x_0$ -> $x_t$ 로 한번에 noise를 주입하는 수식을 제공합니다. (실제 학습시에는 이 수식을 이용합니다.)
우리의 목표 (reverse process를 학습하기!)
- 위 그림 왼쪽의 noise image을 샘플링해서 시작점으로 사용하여, 기 학습한 reverse process를 거치면,
  - 오른쪽 데이터 분포 그래프의 확률대로 이미지가 생성되는 생성 모델을 학습하고 싶음!
어떻게 학습하는데?
- 1. 원본 이미지( $x_0$ )에서, 점진적으로 noise image ( $x_T$ )로 만드는 forward process는 위 수식처럼 우리가 직접 정의했어. ( $q(x_{t}|x_{t-1})$ )
- 1. 역 과정인, $q(x_{t-1}|x_{t})$ 를 우리가 알 수 있다면, reverse process를 알 수 있는 것이야. 하지만, $q(x_{t-1}|x_{t})$ 는 직접 알 수 없어. 그래서,,,
- 1. $q(x_{t-1}|x_{t})$ 와 최대한 유사하게 되는걸 학습 목표 함수로 삼는 $p_{\theta}(x_{t-1}|x_{t})$ 를 딥러닝 네트워크로 학습하자!
[참고] 아래의 본격적 내용들을 이해하기 위해 중요한 정보
- $q(x_{t-1}|x_{t})$ 도 gaussian distribution이야. 단 아래의 조건 하에서,
  - $β$ ₜ가 매우 작을때만 성립
  - 다른 말로 하면, forward process가 매우 작은 양의 gaussian noise로 구성될 때 성립
  - 증명은 pass !
- 그래서 우리는 $p_{\theta}(x_{t-1}|x_{t})$ 도 gaussian distribution 으로 설정하고 학습할것임!

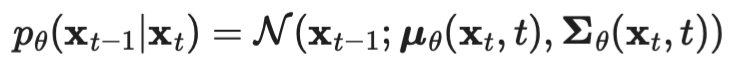
2. 구체적으로 학습 어떻게 하는데?

2.1. 두괄식 결론부터

학습 과정과, inference 과정은 아래의 그림으로 정리 가능하다.
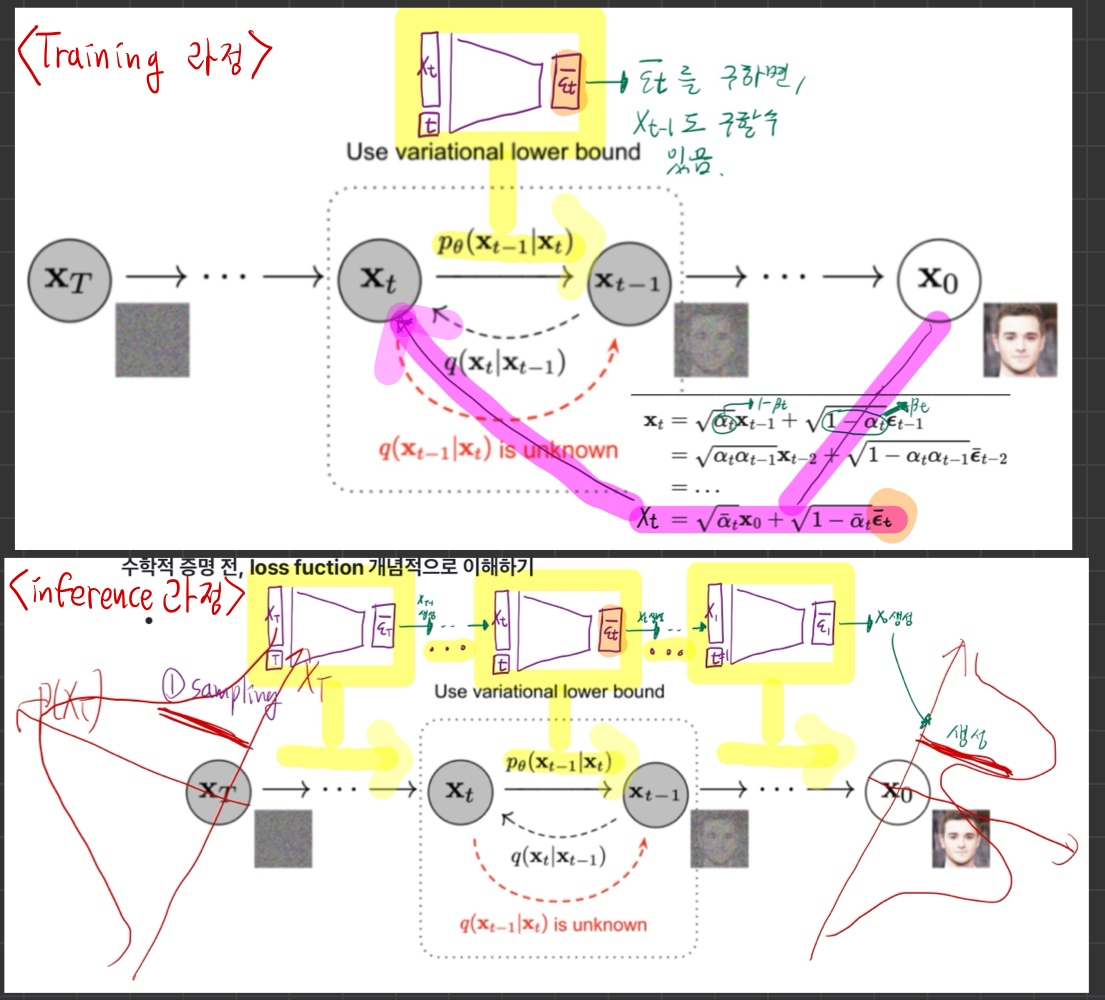
용어 정리: sampling = inference
왜 위 그림처럼 되는지를 이제 하나하나 살펴보자.

2.2. 왜 딥러닝 모델이 $x_{t-1}$ 을 구하기 위해서, $\bar{ϵ_t}$ 출력해?

학습 목표 함수를 공부해보면 답이 나온다.
바로 위 글에서 $q(x_{t-1}|x_{t})$ 와 최대한 유사하게 되는걸 학습 목표 함수로 삼는 $p_{\theta}(x_{t-1}|x_{t})$ 를 딥러닝 네트워크로 학습하자! 라는 목적에 따르면,
- 학습 목표 함수는 아래와 같은 형태
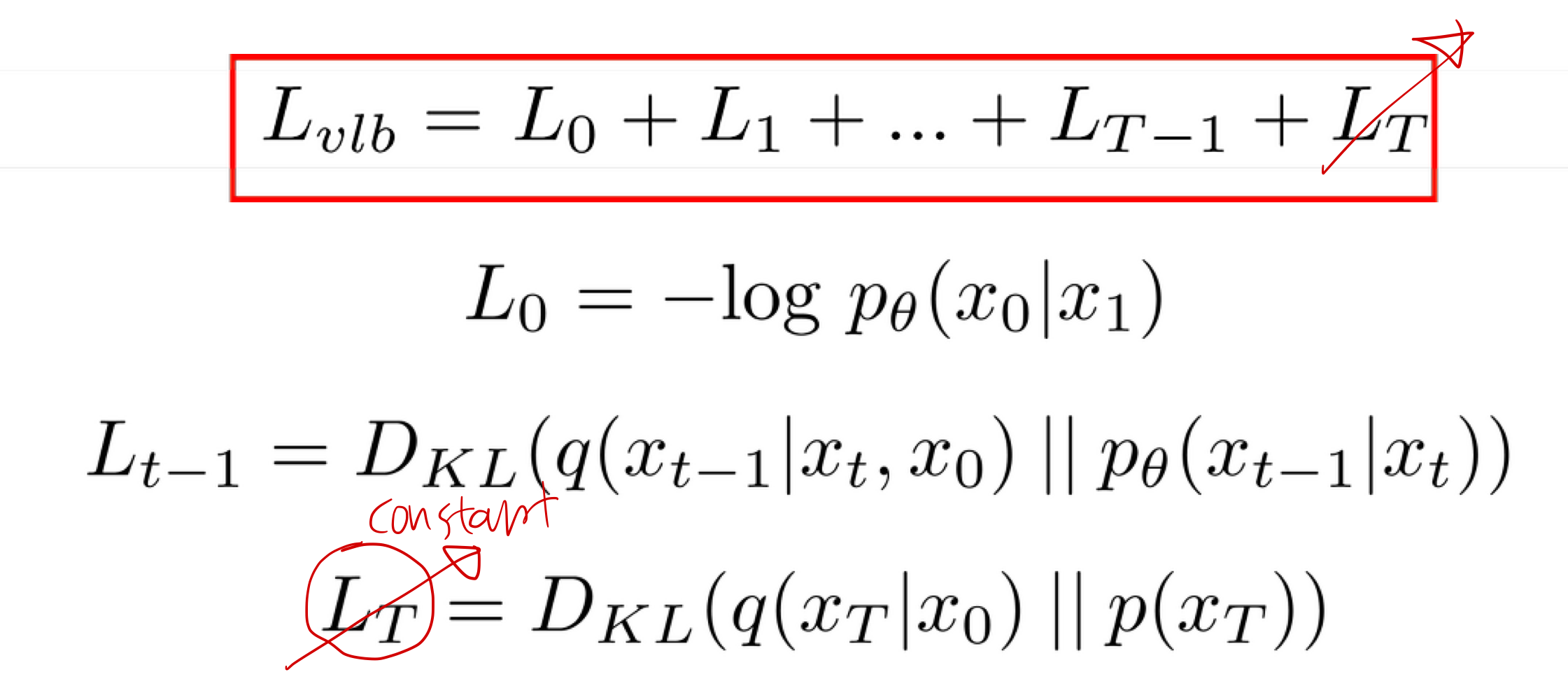
위 수식을 학습 목표로 삼고, $p_{\theta}(x_{t-1}|x_{t})$ 를 딥러닝 네트워크로 학습하자!
- 왜 KL-divergence 항에 $q(x_{t-1}|x_{t})$ 대신 $q(x_{t-1}|x_{t}, x_0)$ 가 쓰였는지는 차차 설명할 것입니다.
- 왜 수학적으로 위 수식을 목표 함수로 쓰는지, 그 이유와 증명도 차차 설명할 것입니다.
아까, 위에서 $q(x_{t-1}|x_{t})$ , $p_{\theta}(x_{t-1}|x_{t})$ 가 ( $β$ ₜ가 매우 작을때) gaussian distribution 이라고 했습니다.
그러므로, 우리는 $q(x_{t-1}|x_{t}, x_0)$ 역시, gaussian distribution이라고 가정합니다. (이 가정은 수학적으로 증명되지 않은 가정)
- 이렇게 가정하는 이유는, 우리가 $q(x_{t-1}|x_{t}, x_0)$ 를 gaussian distribution이라고 가정하면, 이 분포의 평균과 분산을 수학적으로 계산할 수 있기 때문입니다.
- 유도/증명 과정은 Appendix A를 참고하세요.
최종적으로, 계산으로 도출한 $q(x_{t-1}|x_{t}, x_0)$ 의 평균과 분산은 아래와 같다!
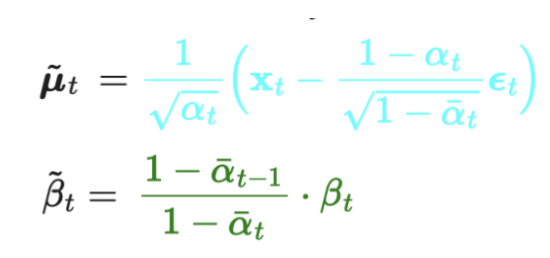
결론적으로, 우리는 $q(x_{t-1}|x_{t}, x_0)$ gaussian의
- 분산은 알파(베타) 값만 필요하므로, 이미 알고 있는 값이고,
- 평균은 ϵ_t만 우리가 구할 수 있으면 된다!
왜냐, 알파(베타)는 forward process에서 sampling해서 쓴 것을 그대로 다시 이용하는 것이기 때문이다!
- 보충 설명
  - 알파, 베타는 학습 시, 이미지 1, 2, 3 input에 상관없이, sampling step t 에 의해서만 결정되는 scheduling 을 따름
  - ϵ_t 이미지 1, 2, 3 input이 들어올 때마다, 매번 random sampling 하는 값임
그러므로 우리는, $p_{\theta}(x_{t-1}|x_{t})$ 가 ϵ_t을 정확히 출력하도록 학습할 수 있다면,
- 우리는 $q(x_{t-1}|x_{t}, x_0)$ 의 guassian distribution 의 평균/분산을 알게 되는 것이므로,
  - noise가 낀 이미지의 noise를 점진적으로 제거할 수 있게 된다!
그럼 우리는 이제, ϵ_t을 출력하는 딥러닝 네트워크인 $p_{\theta}(x_{t-1}|x_{t})$ 의 학습 목표 함수를 정의해보자!
- 분산은 우리가 구할 수 있으니까, 평균만 두 분포가 같도록 학습하면 되겠다. 구체적으로는 아래와 같다.

simplification? 왜 하는데?

학습 과정에서, t는 1과 T 사이에서 uniform하게 sampling된다.
Simplified objective는 기존의 training objective에서 가중치를 제거한 형태
이 가중치항은 t에 대한 함수로, t가 작을수록 큰 값을 가지기 때문에
- t가 작을 때 더 큰 가중치가 부여되어 학습된다.
- 즉, 매우 작은 양의 noise가 있는 데이터에서 noise를 제거하는데 집중되어 학습된다.
이로 인해, 매우 작은 t에서는 학습이 잘 진행되지만, 큰 t에서는 학습이 잘 되지 않기 때문에
- 가중치항을 제거하여 큰 t 에서도 학습이 잘 진행되도록 한다.

목표 함수 최종 정리

최종적으로 정리하면, 위에서 구한 Loss Function은 아래와 표현 가능하다.
$\mathcal{L}_{\text{simple}}(\theta) \;=\; \mathbb{E}_{\,t\sim\mathcal{U}\{1,\dots,T\},\; x_{0}\sim q(x_{0}),\; \epsilon\sim\mathcal{N}(0,I)} \Bigl[ \lambda_t\,\bigl\| \epsilon \;-\; \epsilon_{\theta}(x_t,\,t) \bigr\|_2^{2} \Bigr],$

2.3. 학습 목표를 다른 관점에서 보자! 학습 데이터셋분포를 최대한 잘 모사한 생성 모델 만들기!

생성 모델의 목표는 학습 데이터셋의 분포를 최대한 유사하게 모사하는 것이다.
- 이를 멋지게 수학적으로 표현하면 $log(p_{\theta}(x_0))$ 를 최대화 하는 것이다.
  - 여기서 $x_0$ 는 우리 학습 데이터셋에 있는 많은 원본 데이터들이다.
즉 우리의 학습 목표는 $log(p_{\theta}(x_0))$ 를 최대화하는 것이라고도 볼 수 있는데,
- 이를 직접 수식으로 계산하기 어려워서,
  - 우리는 $log(p_{\theta}(x_0))$ 의 하한 값(Lower Bound)을 수학적으로 도출한 뒤, 이 하한 값을 극대화하는 목표함수로 삼는다.
  - 이를 유식한 표현으로는 Variaional Lower Bound(VLB) (혹은 Evidence Lower B)und(ELBO) )이라고 한다.

수학적 증명하기

아래 과정 1, 과정 2 수학적 증명은 저도 잘 모릅니다.
아래 결론 목표 함수 탭을 보면, 우리가 위에서 설명했던 diffusion process의 목표 함수와 일치한다는 것만 알고 가면 됩니다.
- 다른 말로 하면, 우리 diffusion process의 목표 함수는 아래의 역할도 수행합니다.
  - 학습 데이터셋분포를 최대한 잘 모사한 생성 모델 만들기

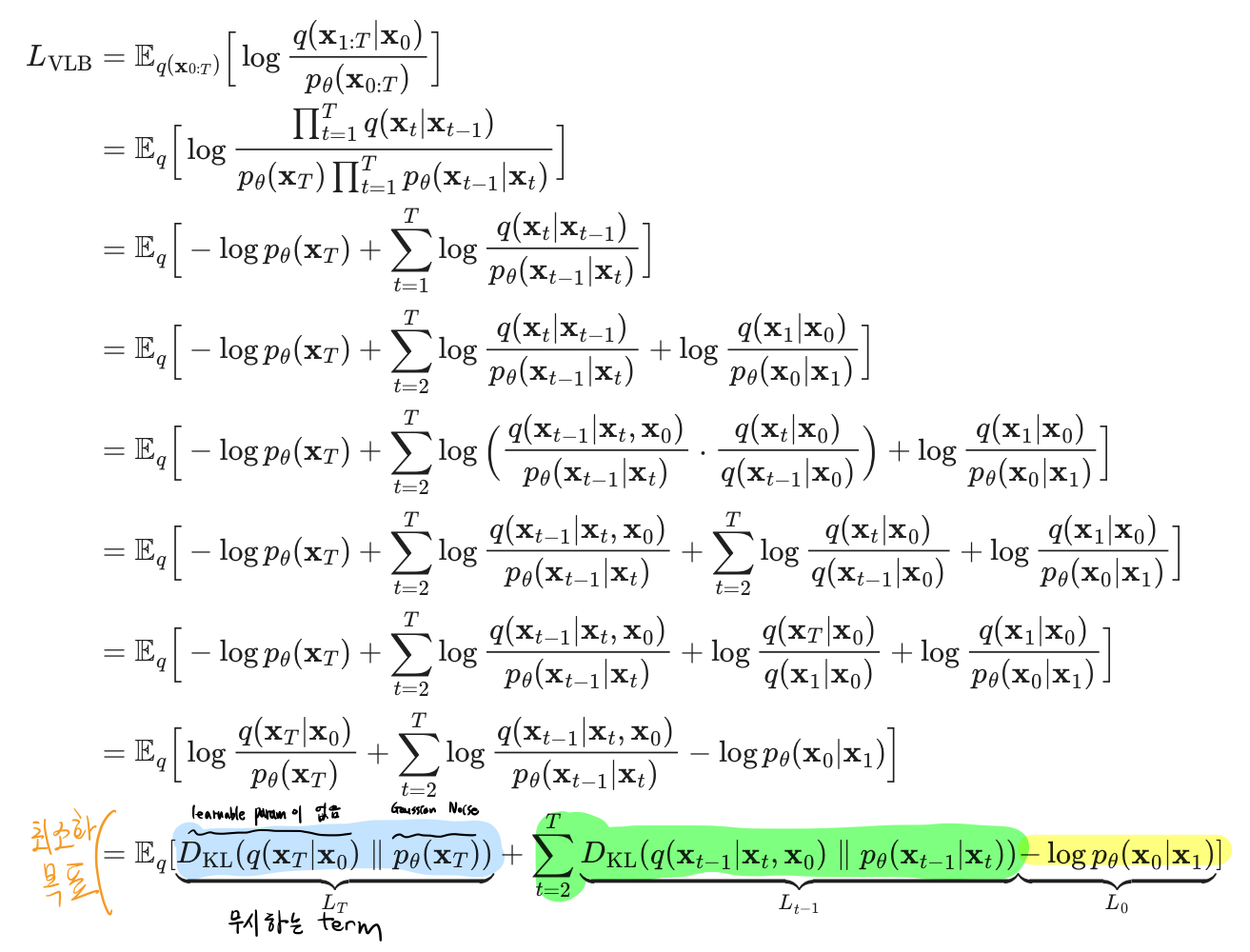
과정 1: Variational Lower Bound 유도하기

방법 1
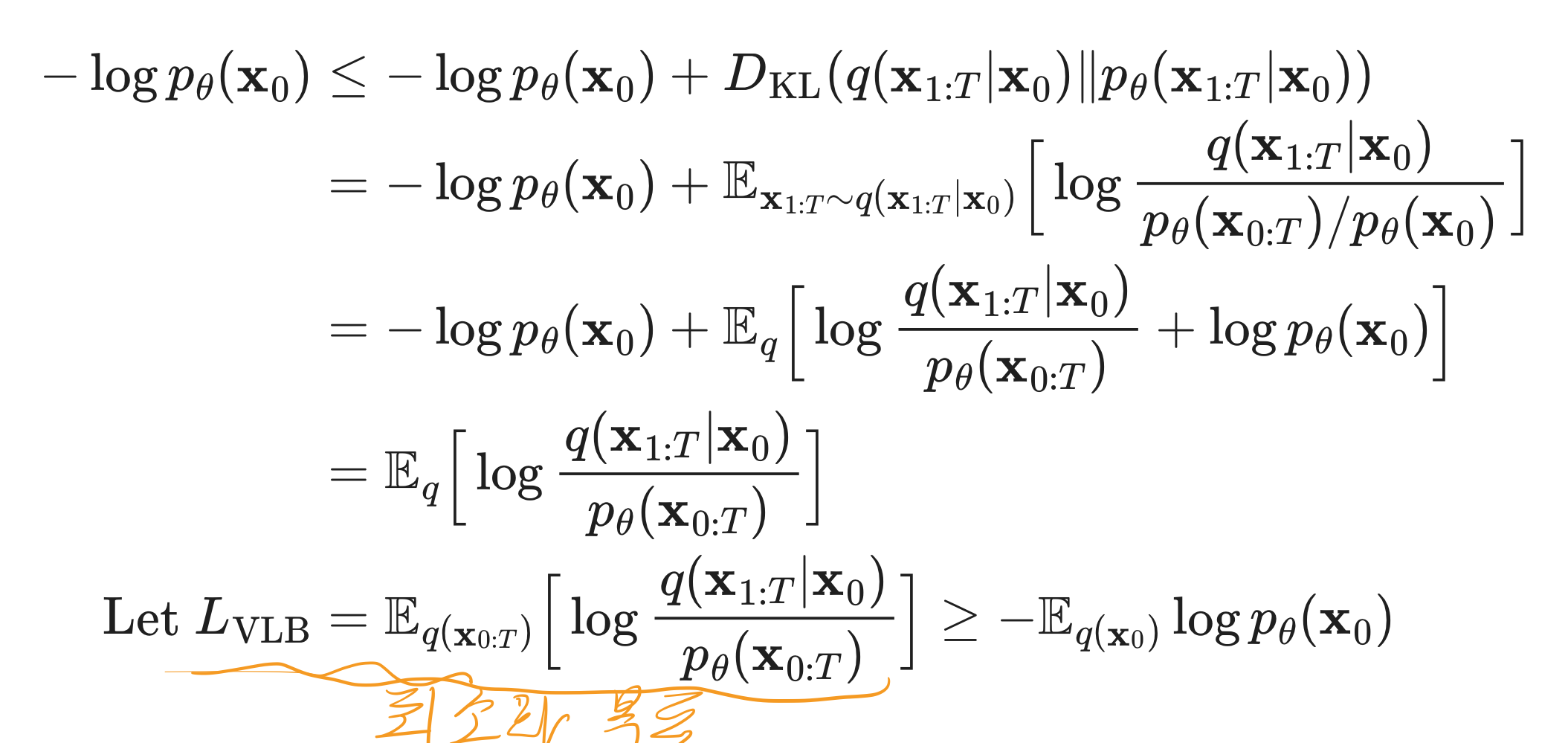
방법 2

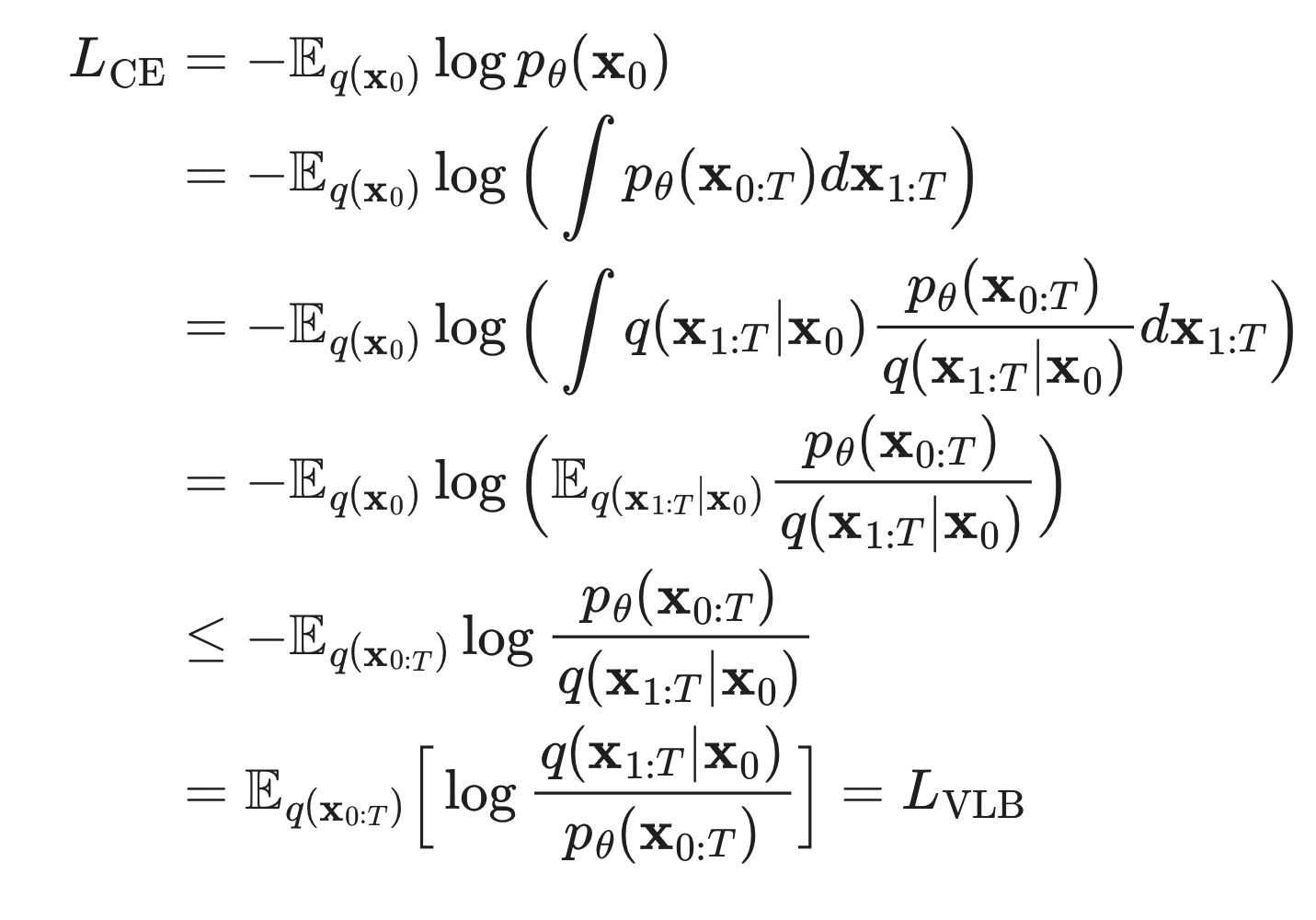
과정 2: Variational Lower Bound를 예쁘게 정리하기

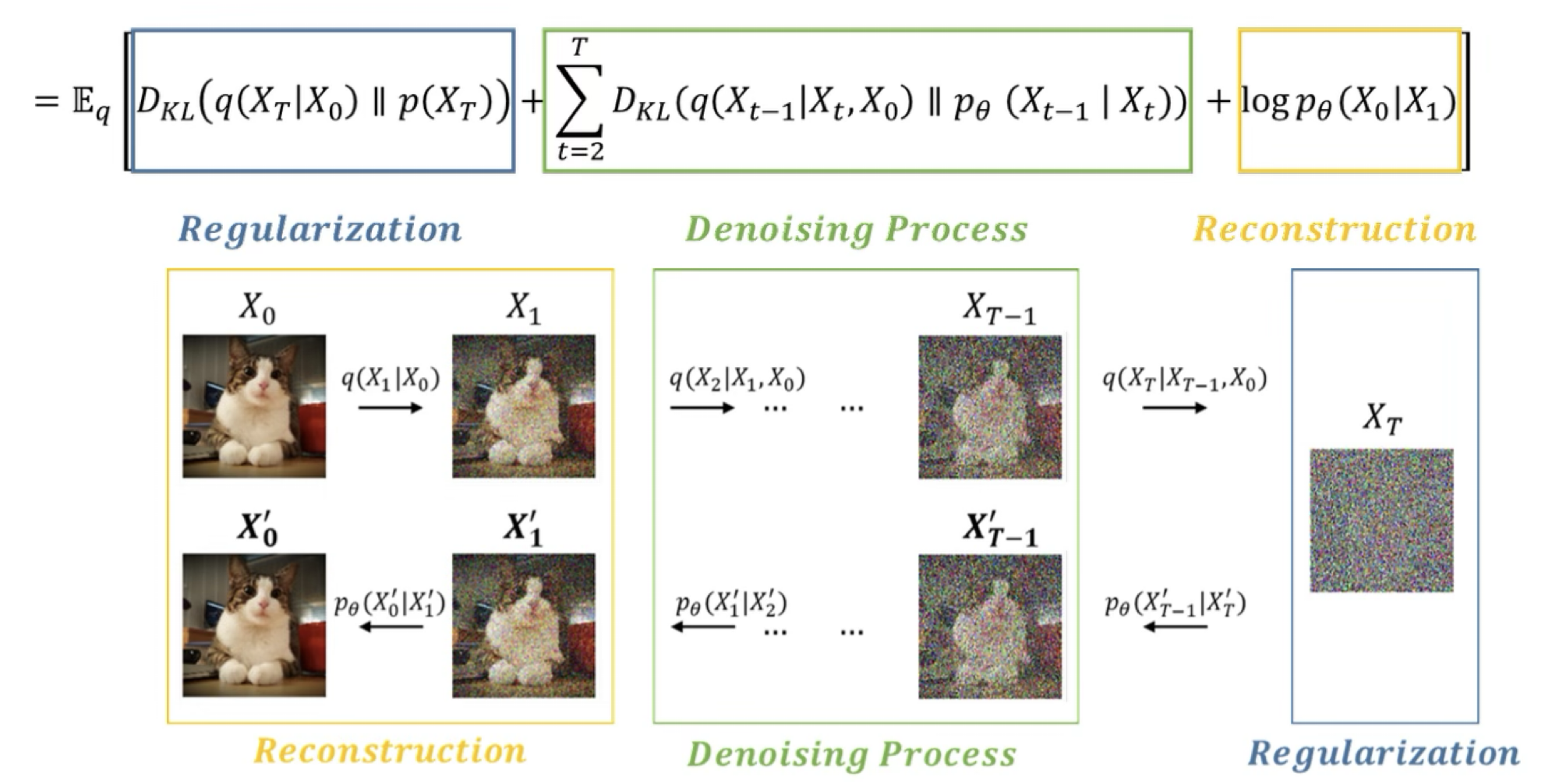
결론 목표 함수

파란색: Regularization Term

Regularization Term의 경우 삭제함. (아래의 이유 떄문)
- Diffusion과정 자체가 gaussian의 가정을 기반으로 하고,
- T가 무한대로 갈 때 istropic gaussian이 된다는 가정을 두고 있음
즉, 굳이 가우시안을 따르도록 regularization을 해줄 필요가 없기에 이는 삭제 된다.

노란색: Reconstruction Term

실제로 Diffusion이라는 물리적 현상 자체가 인접한 small time step 에 대해서 small gaussian noise를 주입해주는 과정으로 진행되기에 x0와 x1에서의 차이는 거의 없다.
실제로 DDPM에서는 이에 대해서 ablation study또한 진행했고, reconstruction term은 너무 작기에 학습에 유의미한 영향을 끼치지 않기에 제거했다.

최종 학습/inference 과정 정리

DDPM에서는 βₜ를 학습 가능한 상태로 만드는 대신 상수로 고정하고, Σₜ(xₜ, t)을 다음과 같이 설정했습니다:
$Σₜ(xₜ, t) = σₜ²I$
- 여기서 σₜ는 학습되지 않고 , $σₜ= βₜ$
- 여기서 주목할 점: 위에서 유도한 분산인 아래 수식을 쓰지 않는다는 점
분산을 학습하지 않는 이유: 대각 분산 Σₜ를 학습하면 학습이 불안정해지고 샘플 품질이 저하된다고 판단

3. DDPM의 성능 평가

DDPM은 높은 FID와 IS 점수를 기록했지만 높은 log-likelihood를 달성하는 데는 실패
높은 FID와 IS 점수:
- 생성된 이미지의 현실성(진짜 같이 보이나?)가 높고,
- 생성된 이미지의 다양성이 높다!
log-likelihood 실패:
- 모델이 데이터의 실제 분포를 정확하게 학습하지 못했음을 나타냄
따라서, DDPM이 다양하고 시각적으로는 뛰어난 이미지를 생성하지만, 확률적 모델링 측면에서는 한계가 있음을 알 수 있습니다.

Appendix

A. $q(x_{t-1}|x_{t}, x_0)$ 의 평균과 분산 유도하기

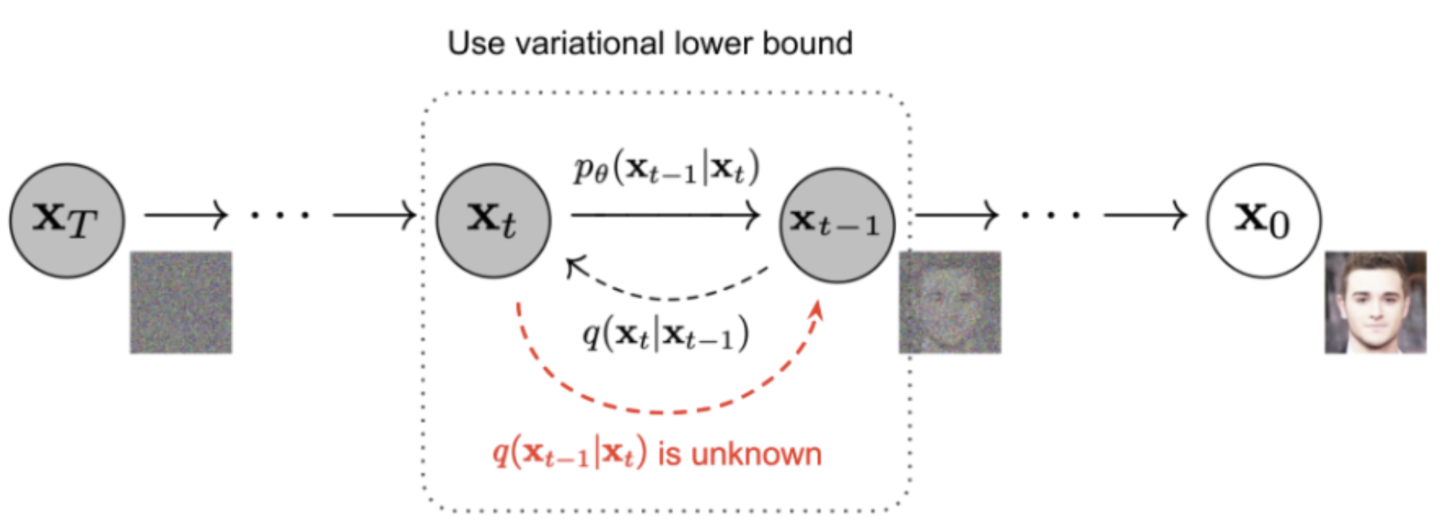
우리가 구하고 싶은 것: q(x_t-1|x_t)
- 우리는 x_0의 정보를 학습 시 알고 있고,
- x_0를 조건으로 할 때 -> reverse conditional probability의 가우시안 분포의 평균 분산이 수학적으로 계산 가능하다고 합니다.
- 그래서 q(x_t-1|x_t, x_0)을 구하는 것으로 목표를 바꿔봅시다.
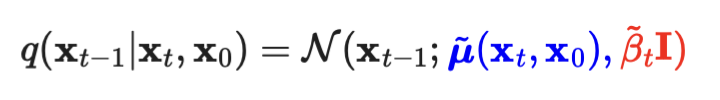
우리는 위 식에서, guassian 분포의 평균(파란색)과 분산(빨간색)을 구하는 것이 목표입니다.
자 이제, 수학적으로 평균(파란색)과 분산(빨간색)을 구해봅시다.
들어가기 전에: 다변수 정규분포의 확률 밀도 함수 수식
위 다변수 정규분포의 pdf 정의와, 자연로그의 성질을 이용하면, 아래와 같이 계산된다.
위 전개한 마지막 식으로부터 q(x_t-1 | x_t) gaussian의 평균(파란색)과 분산(빨간색)을 정리해보면, 아래와 같다.
분산 / 평균 순서